A uiform ring of mass M and radius R is placed directly above a uniform sphere of mass 8M and same radius R. The centre of the sphere. The gravitational atraction between the sphere and the ring is
8GM2R2
2GM2√3R2
3GM22R2
√32GM2R2
The correct Answer is:D
To find the gravitational attraction between a uniform ring of mass M and radius R placed directly above a uniform sphere of mass 8M and the same radius R, we can follow these steps:
1. Identify the Gravitational Field Due to the Sphere:
The gravitational field E at a distance h above the center of a uniform sphere is given by the formula:
E=GMr2
where G is the gravitational constant, M is the mass of the sphere, and r is the distance from the center of the sphere to the point where the field is being calculated.
2. Calculate the Gravitational Field at the Position of the Ring:
Since the ring is placed directly above the center of the sphere at a distance R (the radius of the sphere), the gravitational field at the location of the ring is:
E=G(8M)R2
Simplifying this gives:
E=8GMR2
3. Calculate the Gravitational Force on the Ring:
The gravitational force F acting on the ring due to the gravitational field created by the sphere can be calculated using the formula:
F=m⋅E
where m is the mass of the ring. Substituting the expression for E:
F=M⋅8GMR2
Simplifying this gives:
F=8GM2R2
4. Final Result:
Therefore, the gravitational attraction between the sphere and the ring is:
F=8GM2R2
Conclusion:
The gravitational attraction between the sphere and the ring is 8GM2R2.
The gravitational field E at a distance h above the center of a uniform sphere is given by the formula:
E=GMr2
where G is the gravitational constant, M is the mass of the sphere, and r is the distance from the center of the sphere to the point where the field is being calculated.
Since the ring is placed directly above the center of the sphere at a distance R (the radius of the sphere), the gravitational field at the location of the ring is:
E=G(8M)R2
Simplifying this gives:
E=8GMR2
The gravitational force F acting on the ring due to the gravitational field created by the sphere can be calculated using the formula:
F=m⋅E
where m is the mass of the ring. Substituting the expression for E:
F=M⋅8GMR2
Simplifying this gives:
F=8GM2R2
Therefore, the gravitational attraction between the sphere and the ring is:
F=8GM2R2
The gravitational attraction between the sphere and the ring is 8GM2R2.
Topper's Solved these Questions
Similar Questions
A uniform rig of mas m and radius a is placed directly above a uniform sphre of mass M and of equyal radius. The centre of the ring is at a distance √3 a from the centre of the sphere. Find the gravitational foerce exerted by the sphere on the ring.
View SolutionA uniform ring of mass 2m and radius a is placed directly above the uniform sphere of mass M and of same radius. The centre of ring is at distance √3a from the centre of sphere. The gravitational force exerted by the sphere on the ring is NGMma2 units. Calculate is the value of N?
View Solution
Knowledge Check
- Question 1 - Select One
A uniform ring of mass M and radius R is placed directly above a uniform sphere of mass 8M and of same radius R. The centre of the ring is at a distance of d=√3R from the centre of the sphere. The gravitational attraction between the sphere and the ring is
AGM2R2B3GM22R3C2GM2√2R2D√3GM2R2 - Question 2 - Select One
A uniform ring of mass M and radius R is placed directly above a uniform sphere of mass 8M and of same radius R. The centre of the ring is at a distance of d=√3R from the centre of the sphere. The gravitational attraction between the sphere and the ring is
AGM2R2B3GM2R3C2GM2√2R2D√3GM2R2 - Question 3 - Select One
For a uniform ring of mass M and radius R at its centre
Afield and potential both are zeroBfield is zero but potential is GMRCfield is zero but potential is −GM/RDmagnitude of field is GMR2 and potential −GMR
A uniform metal sphere of radius R and mass m is surrounded by a thin uniform spherical shell of same mass and radius 4R. The centre of the shell C falls on the surface of the inner sphere. Find the gravitational fields at points A and B.
 View Solution
View SolutionA uniform ring of mass m and radius 3a is kept above a sphere of mass M and radius 3a at a distance of 4a (as shown in figure) such that line joining the centres of ring and sphere is perpendicular to the plane of the ring. Find the force of gravitational attraction between the ring and the sphere.
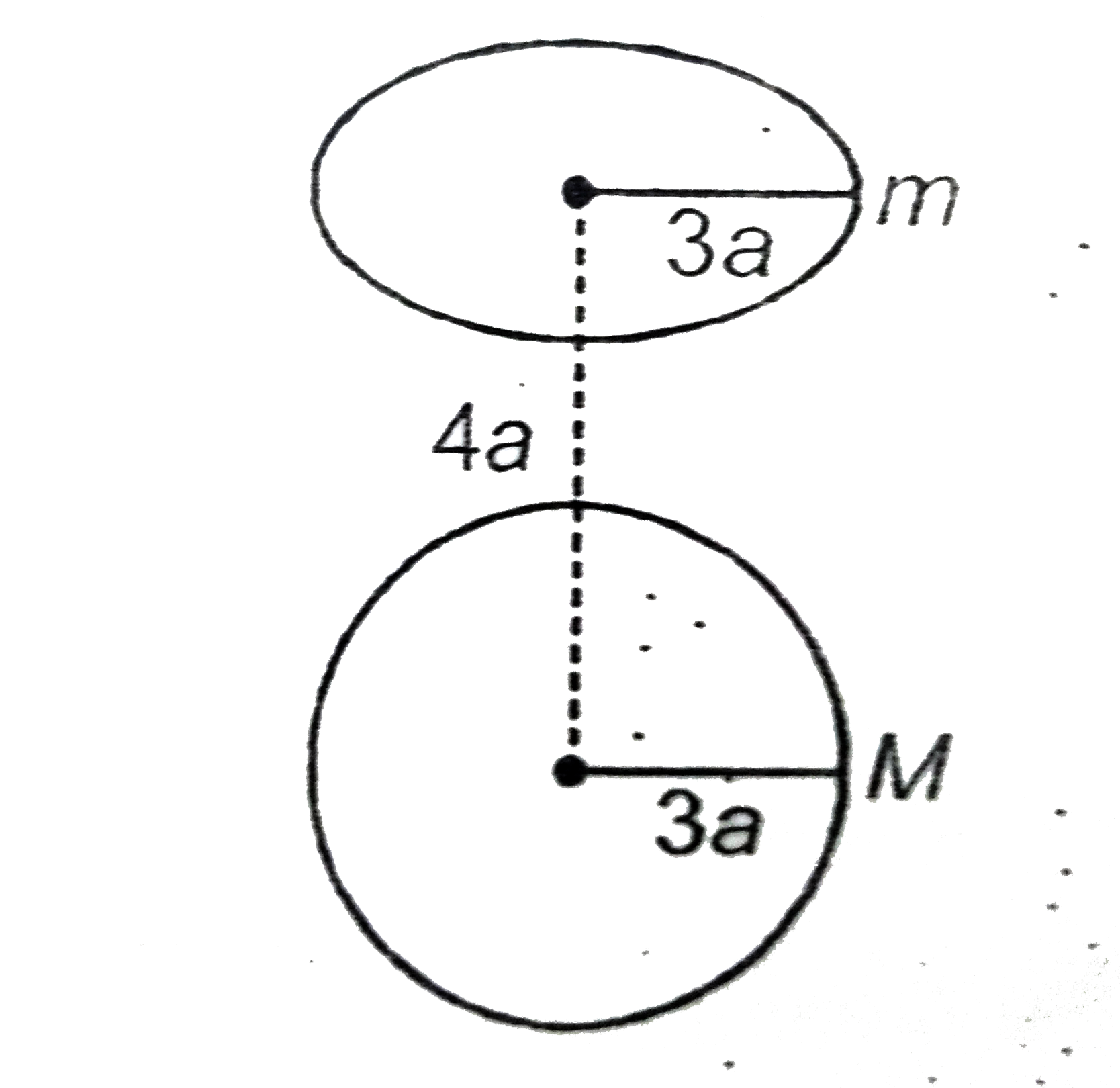 View Solution
View SolutionA particle of mass m is located outside a uniform sphere of mass M at a distance r from its centre. Find:
(a) the potential energy of gravitational interaction of the particle and the sphere,
(b) the gravitational force which the sphere exerts on the particle.View SolutionThe gravitational field due to an uniform solid sphere of mass M and radius a at the centre of the sphere is
View SolutionThe moment of inertia of a solid sphere of mass ‘M' and radius 'R' about a tangent to the sphere is
View Solution

