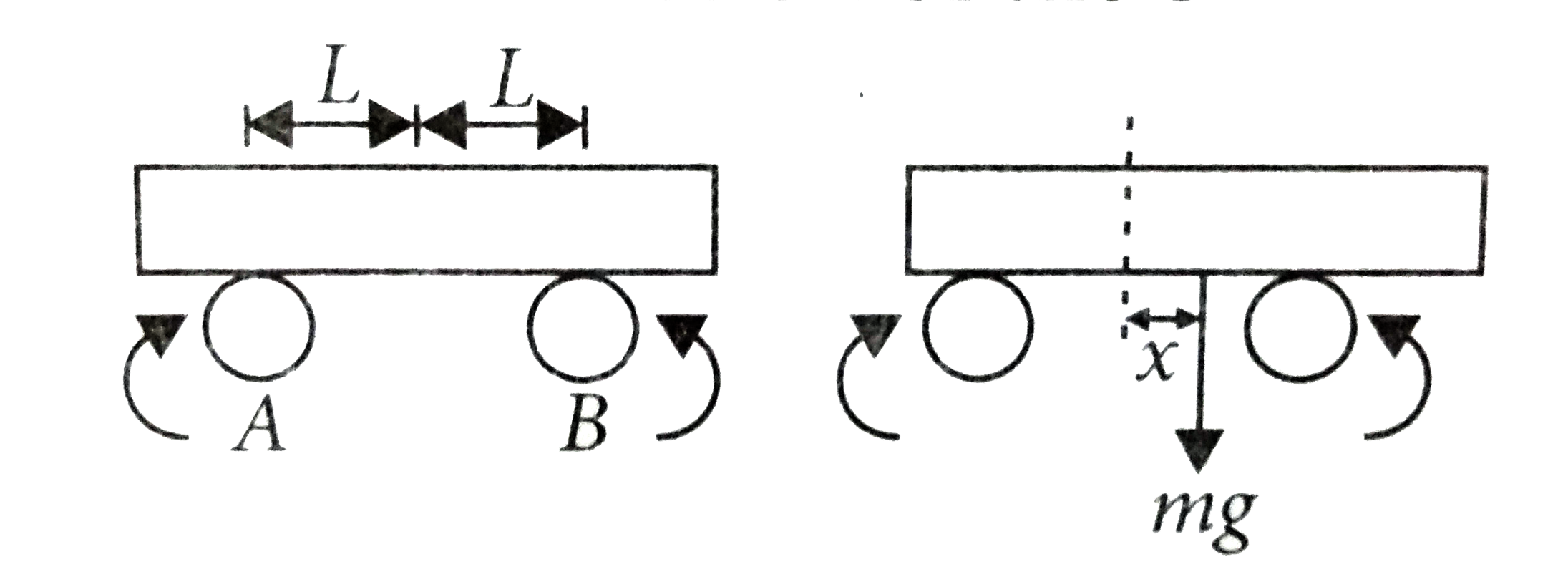
A uniform bar with mass m lies symmetrically across two rapidly rotating fixed rollers, A and B with distance L=2.0 cm between the bar's centre of mass and each roller. The rollers, whose directions of rotation are shown in figures slip against the bar with coefficient of kinetic friction μk=0.40. suppose the bar is displaced horizontally by the distance x as shown in figure and then released. the angular frequency ω of the resulting horizontal simple harmonic motion of the bar is (in rad s−1)
(1) This situation seems very different from other SHM situations we have analyzed. However, the key idea here is that we can find ω if we find an expression for the horizontal acceleration a of the bar as a function of x and then compare it with a=−ω2x.
(2) Since vertical forces (as shown in Fig.15.14b), horizontal frictional forces, and torques all act on the bar, we shall apply Newton.s second law both vertically and horizontally, and then in angular form about one of the contact points between bar and roller.
Calculations: The vertical force acting on the bar are the gravitational force →Fg (with magnitude mg) and supporting forces →FA due to roller A and →FB due to roller B. Since there is no vertical acceleration of the bar. Newton.s second law for components along a vertical y axis (Fnet, y=may) gives us
FA+FB−mg=0
The horizontal forces acing on the bar are the kinetic frictional forces FkA=μkFA (toward the right) due to roller A and fkB=μkFB (toward the left) due to roller B. Thus,

Figure 15.14 (a) A bar is in equilibrium on two rotating rollers. A and B, that slip beneath it. (b) The bar is displaced from equilibrium by a distance x and then released.
Newton.s second law for components along a horizontal x axis (Fnet.x=max) gives us
μkFA−μkFB=ma
a=μkFA−μkFBm
We now consider torques about an axis perpendicular to the plane of Fig. 15.14 and through the contact point between the bar and roller A. The bar experiences no angular acceleration about that axis, so Newton.s second law for torque about an axis (τnet=Ia) gives us
FA(0)+FB2L−mg(L+x)+fkA(0)+fkB(0)=0
where the forces →FA,→FB,m→g,→fkA,and→fkB have moment arms about that axis of 0, 2L, L + x, 0 and 0, respectively. Solving Eq.15.36 for FB and then solving Eq.15.34 for FA we find
FB=mg(L+x)2LandFA=mg(L−x)2L
Substituting these results into Eq.15.35 yields.
a=μkgLx
Thus ω=√μkgL=√(0.40)(9.8m/s2)0.020m
= 14 rad/s
Learn: Another important point is that the rollers will be experiencing kinetic friction which cal slow them dwon. There must be some external torque on the rollers to maintain the motion of the rollers.
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - OSCILLATIONSEXERCISE - Checkpoint8videos
OSCILLATIONS
- BOOK - RESNICK AND HALLIDAYCHAPTER - OSCILLATIONSEXERCISE - Problems39videos
OSCILLATIONS
- BOOK - RESNICK AND HALLIDAYCHAPTER - MOTION IN TWO AND THREE DIMENSIONSEXERCISE - PRACTICE QUESTIONS (MATRIX-MATCH)10videos
MOTION IN TWO AND THREE DIMENSIONS
- BOOK - RESNICK AND HALLIDAYCHAPTER - PHOTONS AND MATTER WAVESEXERCISE - PRACTICE QUESTIONS(Integer Type)4videos
PHOTONS AND MATTER WAVES
Similar Questions
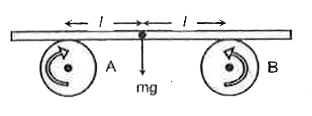
A uniform bar with mass m lies symmetrically across two rapidly rotating fixed rollers. A and B with distance 'l' between the bars centre of mass and each roller. The rollers whose direction of rotation are shown in figure slip against the bar with coefficient of friction μ. Suppose the bar is displaced horizontally by a small distance 'x' and then released, find the time period of oscillation.
 View Solution
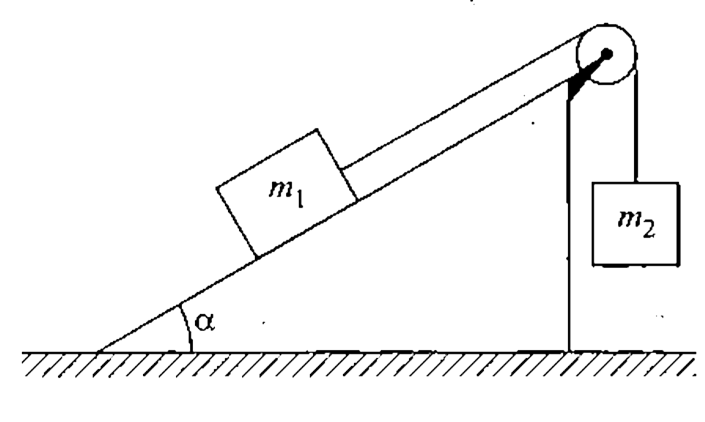
View SolutionFind the acceleration of the prism of mass M and that of the bar of mass m shown in figure.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A block with mass 0.50kg is forced against a horizontal spring of negligible mass , compressing the spring a distance of 0.20m (figure). When released, the block moves on a horizontal table top for 1.00N/m. What is the coefficient of kinetic friction μk, between the block and the block and the table?
 A0.40B0.50C0.25Dnone of these
A0.40B0.50C0.25Dnone of these - Question 2 - Select One
A thin bar of mass m and length l is free to rotate about a fixed horizontal axis through a point at its end. The bar is brought to a horizontal position. (θ=90∘) and then released. The angular velocity when it reaches the lowest point is
Adirectly proportional to its length and inversely proportional to its massBindependent of mass and inversely proportional to the square root of its lengthCdependent only upon the acceleration due to gravity and the mass of the barDdirectly proportional to its length and inversely proportional to its length and inversely proportional to the acceleration due to gravity. - Question 3 - Select One
Two short bar magnets of equal dipole moments 'M' each are fastened perpendicular at their centers as shown in figure. The magnitude of the magnetic field at 'P' at a distance d from their common centre as shown in figure is
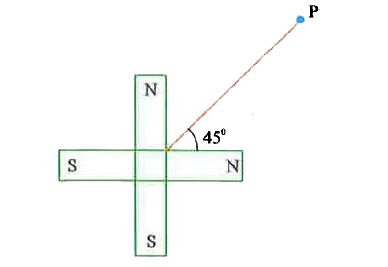 Aμ04πMd3Bμ04π2√2Md3Cμ04π2Md3Dμ02πMd3
Aμ04πMd3Bμ04π2√2Md3Cμ04π2Md3Dμ02πMd3
the position vector of the centre of mass lt
→
r cm of an asymmetric uniform bar of negligible area of cross - section as shown in figure is :
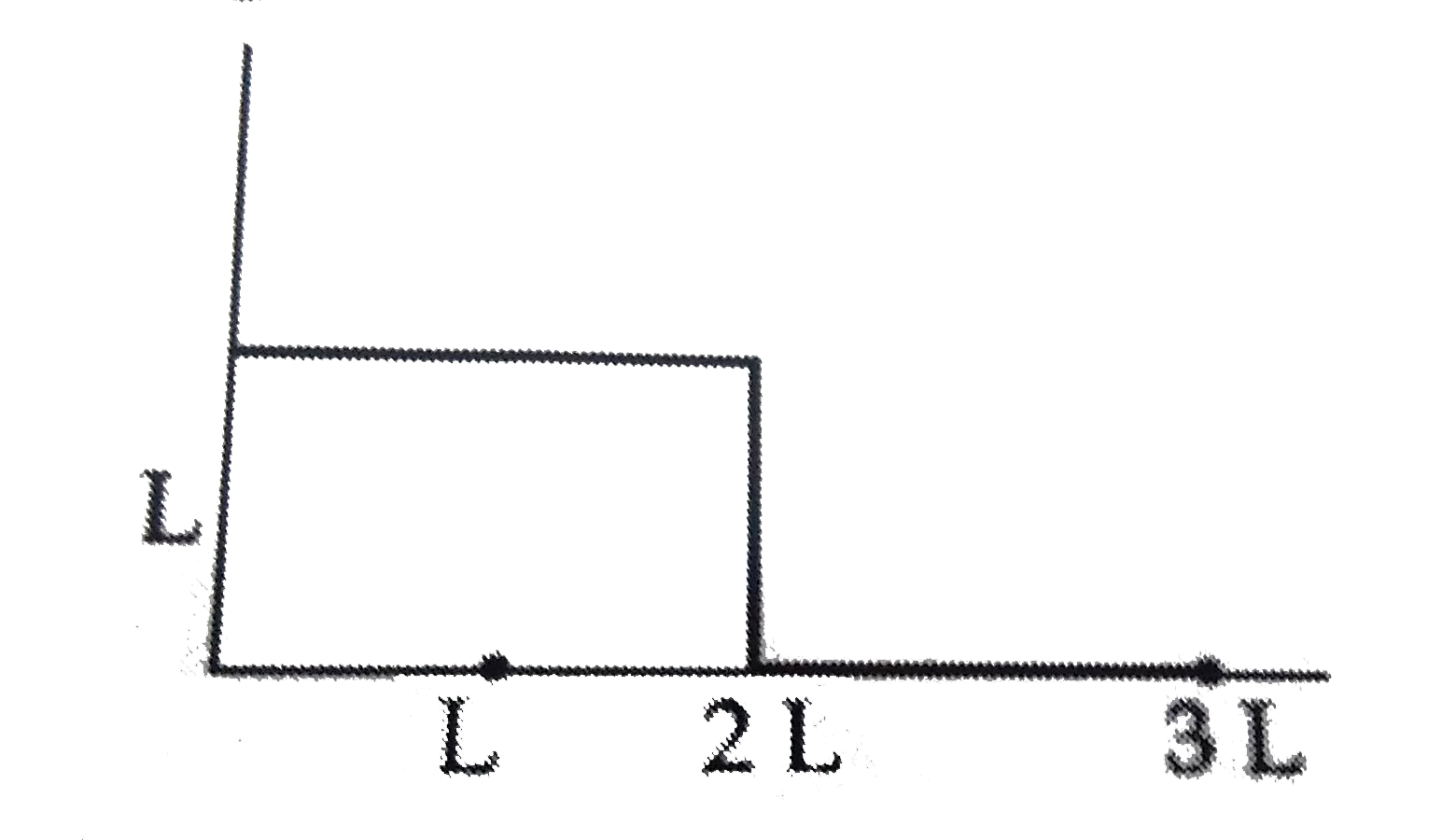 View Solution
View SolutionTwo bar of identical dimensions are kept as shown in figure. If K1 and K2are their coefficients of thermal conductivities, then equivalent K
 View Solution
View SolutionA uniform rod of length L rests against a smooth roller as shown in figure. Find the friction coefficient between the ground and the lower end if the minimum angle that rod can make with the horizontal is θ.
 View Solution
View SolutionTwo uniform thin rods each of length L and mass m are joined as shown in the figure. Find the distance of centre of mass the system from point O
 View Solution
View SolutionA bar of mass m and length l is in pure translational motion with its centre of mass moving with a velocity v. It collides and sticks to another identical bar at rest as shown in the figure. Assuming that after the collision the system of the two bars becomes one composite bar of length 2l, then the angular velocity of the composite bar will be
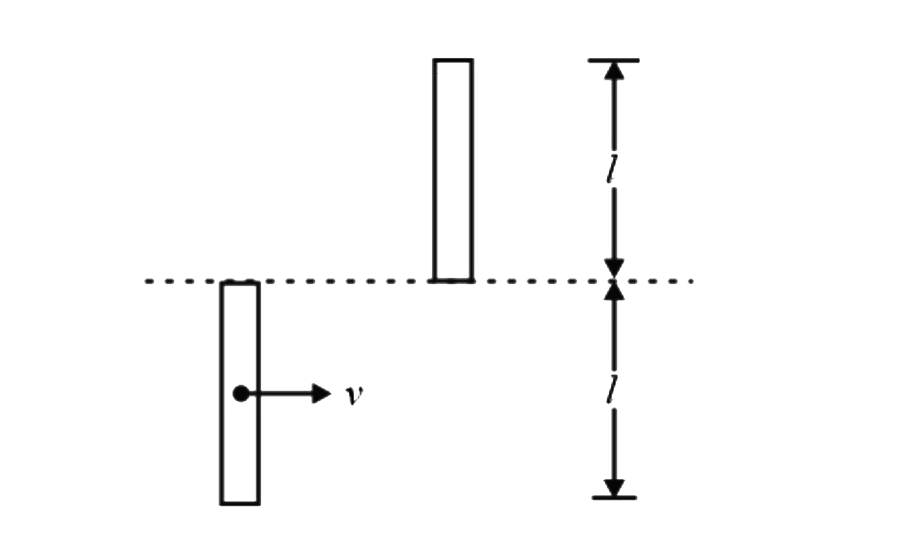 View Solution
View Solution

