A particle undergoes damped harmonic motion. The spring constant is 100N/m, the damping constant is 8.0×10−3kgm/s, and the mass is 0.50kg. If the particle starts at its maximum displacement, x= 1.5m at time t=0, what is the particle's position at t= 5.0s?
−1.5m
−0.73m
0m
0.75m
The correct Answer is:B
Topper's Solved these Questions
- OSCILLATIONSBOOK - RESNICK AND HALLIDAYCHAPTER - OSCILLATIONSEXERCISE - Problems
39 Videos
- MOTION IN TWO AND THREE DIMENSIONSBOOK - RESNICK AND HALLIDAYCHAPTER - MOTION IN TWO AND THREE DIMENSIONSEXERCISE - PRACTICE QUESTIONS (MATRIX-MATCH)
10 Videos
- PHOTONS AND MATTER WAVESBOOK - RESNICK AND HALLIDAYCHAPTER - PHOTONS AND MATTER WAVESEXERCISE - PRACTICE QUESTIONS(Integer Type)
4 Videos
Similar Questions
Vx is the velocity of a particle of a particle moving along the x−axis as shown. If x=2.0m at t=1.0s, what is the position of the particle at t=6.0s?

View SolutionA block of mass 1kg is connected with massless spring of constant 100N/m .At t=0 ,a constant force F=10N is applied on the block. The spring is in its natural length at t=0.The speed of particle at x=6cm form mean position is
View Solution
Knowledge Check
Vx is the velocity of a particle of a particle moving along the x−axis as shown. If x=2.0m at t=1.0s, what is the position of the particle at t=6.0s?
 A−2.0mB+2.0mC+1.0mD−1.0m
A−2.0mB+2.0mC+1.0mD−1.0mIn damped oscillation mass is 1 kg and spring constant = 100 N/m, damping coefficient = 0.5 kg s–1. If the mass is displaced by 10 cm from its mean position that what will be the value of its mechanical energy after 4 seconds ?
A0.67 JB0.067 JC6.7 JD0.5 JFor the small damping oscillator, the mass of the block is 500 g and value of spring constant is k = 50 N/m and damping constant is 10 g s^(-1) The time period of oscillation is (approx.)
A2πsB2π13sCπ5sDπ√5s
A 1.00×10−20kg particle is vibrating with simple harmonic motion with a period of1.00×10−5 sec and a maximum speed of 1.00×103 m/s . The maximum displacement of the particle is
View SolutionA particle with a mass of 3.00×10−20kg is oscillating with simple harmonic motion with a period of 2.00×10−5s and a maximum speed of 1.00×103m/s. Calculate (a) the angular frequency and (b) the maximum displacement of the particle.
View SolutionA particle moves in the x-y plane with a constant acceleration of 1.5m/s2 in the direction making an angle of 37∘ with the x-axis.
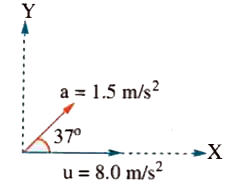
At t=0 the particle is at the origin and its velocity is 8.0m/s along the x- aixs . Find the velocity and the position of the particle at t = 4.0s.
View SolutionA particle of mass 0.25 kg vibrates with a period of 2 s. It its greatest displacement is 0.4 m, its maximum velocity in m/s will be
View SolutionA particle of 0.8 kg is executing S.H.M., Its amplitude is 1.0 metre and time period is 117 seconds. The velocity of the particle at the instant when its displacement is 0.6 metre will be :
View Solution
