A uniform chain of length L is lying partly on a table, the remaining part hanging down from the edge of the table. If the coefficient of friction between the chain and the table is 0.5 what is the minimum length of the chain that should lie on the table, to prevent the chain from slipping down to the ground.
To solve the problem, we need to determine the minimum length of the chain that must lie on the table to prevent it from slipping off. We will denote the total length of the chain as L and the length of the chain on the table as l. The length of the chain hanging off the table will then be L−l.
1. Identify Forces Acting on the Chain:
- The weight of the hanging part of the chain, which is m2g where m2 is the mass of the hanging part and g is the acceleration due to gravity.
- The normal force acting on the part of the chain on the table, which is m1g where m1 is the mass of the part of the chain lying on the table.
- The frictional force opposing the downward motion, which is given by f=μR where μ is the coefficient of friction (0.5) and R is the normal force.
2. Express Masses in Terms of Length:
- The mass of the chain is uniform, so we can express the masses in terms of lengths:
- m1=k⋅l (where k is the mass per unit length)
- m2=k⋅(L−l)
3. Set Up the Equation for Forces:
- The frictional force must balance the weight of the hanging part when the chain is on the verge of slipping:
f=μR
- Substituting the expressions for f and R:
μ(m1g)=m2g
- Cancel g from both sides:
μm1=m2
4. Substitute the Masses:
- Substitute m1 and m2:
μ(k⋅l)=k⋅(L−l)
- Cancel k (assuming k≠0):
μl=L−l
5. Rearranging the Equation:
- Rearranging gives:
l+μl=L
- Factor out l:
l(1+μ)=L
- Solve for l:
l=L1+μ
6. Substituting the Coefficient of Friction:
- Substitute μ=0.5:
l=L1+0.5=L1.5=2L3
Final Answer:
The minimum length of the chain that should lie on the table to prevent it from slipping down is 2L3.
- The weight of the hanging part of the chain, which is m2g where m2 is the mass of the hanging part and g is the acceleration due to gravity.
- The normal force acting on the part of the chain on the table, which is m1g where m1 is the mass of the part of the chain lying on the table.
- The frictional force opposing the downward motion, which is given by f=μR where μ is the coefficient of friction (0.5) and R is the normal force.
- The mass of the chain is uniform, so we can express the masses in terms of lengths:
- m1=k⋅l (where k is the mass per unit length)
- m2=k⋅(L−l)
- The frictional force must balance the weight of the hanging part when the chain is on the verge of slipping:
f=μR
- Substituting the expressions for f and R:
μ(m1g)=m2g
- Cancel g from both sides:
μm1=m2
- Substitute m1 and m2:
μ(k⋅l)=k⋅(L−l)
- Cancel k (assuming k≠0):
μl=L−l
- Rearranging gives:
l+μl=L
- Factor out l:
l(1+μ)=L
- Solve for l:
l=L1+μ
- Substitute μ=0.5:
l=L1+0.5=L1.5=2L3
The minimum length of the chain that should lie on the table to prevent it from slipping down is 2L3.
Topper's Solved these Questions
- FORCE AND LAWS OF MOTIONBOOK - MTG IIT JEE FOUNDATIONCHAPTER - FORCE AND LAWS OF MOTIONEXERCISE - EXERCISE (LONG ANSWER TYPE)
9 Videos
- FORCE AND LAWS OF MOTIONBOOK - MTG IIT JEE FOUNDATIONCHAPTER - FORCE AND LAWS OF MOTIONEXERCISE - EXERCISE (INTEGER VALUE TYPE )
5 Videos
- FORCE AND LAWS OF MOTIONBOOK - MTG IIT JEE FOUNDATIONCHAPTER - FORCE AND LAWS OF MOTIONEXERCISE - EXERCISE (VERY SHORT ANSWER QUESTION)
15 Videos
- FOOTSTEPS TOWARDS NEETBOOK - MTG IIT JEE FOUNDATIONCHAPTER - FOOTSTEPS TOWARDS NEETEXERCISE - Multiple Choice Question
45 Videos
- GRAVITATION BOOK - MTG IIT JEE FOUNDATIONCHAPTER - GRAVITATION EXERCISE - Olympiad/HOTS Corner
20 Videos
Similar Questions
A rough inclined plane is inclined at 30° to the horizontal as shown in the figure. A uniform chain of length L is partly on the inclined plane and partly hanging from the top of the incline. If the coefficient of friction between chain and inclined plane is H, the maximum length of the hanging part to prevent the chain from falling vertically is 30°
View SolutionA uniform rope of total length l is at rest on a table with fraction f of its length hanging (see figure). If the coefficient of friction between the table and the chain is μ then

View Solution
Knowledge Check
A chain is placed on a rough table, partially hanging, as shown in the figure. The coefficient of static friction between the chain and the table is μ = 0.4. If the maximum possible length of the hanging part is x and the length of the chain is L, then what is the value of Lx?
 AμL1+μBμL1−μC(1−μ)L1+μDμL
AμL1+μBμL1−μC(1−μ)L1+μDμLA homogoneous chain of length L lies on a table. The coefficient of friction between the chain and the table is μ. The maximum length which can hang over the table in equilibrium is
A(μμ+1)LB(1−μμ)LC(1−μ1+μ)LD(2μ2μ+1)LA rope of length 30cm is on a horizontal table with maximum length hanging from edge A of the table. The coefficient of friction between the rope and table is 0.5. The distance of centre of mass of the rope from A is
A5√153cmB5√173cmC5√193cmD7√173cm
A heavy uniform chain lies on horizantal table top. If the coefficient of friction between the chain and the table surface is 0.5, the maximum percentage of the length of the chain that can hang over one edge of the table is
View SolutionA heavy uniform chain lies on horizontal table top. If the coefficient of friction between the chain and the table surface is 0.5, the maximum percentage of the length of the chain that can hang over one edge of the table is
View SolutionA heavy uniform chain lies on horizontal table top. If the coefficient of friction between the chain and the table surface is 0.25, the maximum percentage of the length of the chain that can hang over one edge of the table is
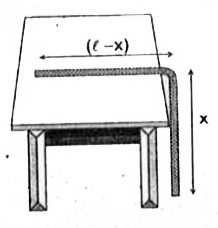
View SolutionA uniform chain of mass m and length I is kept on the table with a part of it overhanging (see figure). If the coefficient of friction between the table and the chain is 1/3 then find the maximum length of the chain that can overhang such that the chain remain in equilibrium.
View SolutionA heavy uniform chain lies on a horizontal table-top. If the coefficient of friction between the chain and table surface is 0.25, then the maximum fraction of length of the chain, that can hang over one edge of the table is
View Solution
