A uniform chain of mass m and length l<πR2 is placed on a smooth hemisphere of radius R with on of its ends fixed at the top of the sphere.
(a) Find the gravitational potential energy of chain assuming base of hemisphere as reference.
(b) what will be the tangential acceleraion of the chain when it starts sliding down.
(c ) If the chain slides down the sphere, find the kinetic energy of the chain when it has slipped through an angle β.
Step by step video & image solution for A uniform chain of mass m and length llt(piR)/(2) is placed on a smooth hemisphere of radius R with on of its ends fixed at the top of the sphere. (a) Find the gravitational potential energy of chain assuming base of hemisphere as reference. (b) what will be the tangential acceleraion of the chain when it starts sliding down. (c ) If the chain slides down the sphere, find the kinetic energy of the chain when it has slipped through an angle beta. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- WORK AND ENERGYBOOK - ANURAG MISHRACHAPTER - WORK AND ENERGYEXERCISE - Level 1
53 Videos
- WORK AND ENERGYBOOK - ANURAG MISHRACHAPTER - WORK AND ENERGYEXERCISE - Level 2
18 Videos
- WORK AND ENERGYBOOK - ANURAG MISHRACHAPTER - WORK AND ENERGYEXERCISE - Matching types problems
14 Videos
- UNIT AND DIMENSIONSBOOK - ANURAG MISHRACHAPTER - UNIT AND DIMENSIONSEXERCISE - Matching Type Problem
4 Videos
Similar Questions
A chain of length l is placed on a smooth spherical surface of radius R with one of its ends fixed at the top of the sphere. What will be the acceleration w of each element of the chain when its upper end is released? It is assumed that the length of the chain l<12πR.
View SolutionA chain of length l is placed on a smooth spherical surface of radius R with one of its ends fixed at the top of the sphere. What will be the acceleration of the each element of the chain when its upper end is released? It is assumed that the length of the chain l<(πR2).
View Solution
Knowledge Check
A chain of length l=πR/4 is placed. On a smooth hemispherical surface of radius R with one of its ends fixed at the top of the sphere. Mass of chain is √πkg and R=1m.(g=10m/s2).
The tangential acceleration of the chain when its starts sliding down.A40π(1−1√2)B20π(1−1√2)C10(1−1√2)DzeroA chain of length l=πR/4 is placed. On a smooth hemispherical surface of radius R with one of its ends fixed at the top of the sphere. Mass of chain is √πkg and R=1m.(g=10m/s2).
The gravitational potential energy of the chain considering reference level at the base of hemisphere isA20 JB20√2JC40 JD40√2JA chain of length l=πR/4 is placed. On a smooth hemispherical surface of radius R with one of its ends fixed at the top of the sphere. Mass of chain is √πkg and R=1m.(g=10m/s2).
If the chain sliped down the sphere, kinetic energy of the chain when it has sliped through an angle θ=π4.A23.4JB63.44JC80 JD97.4J
A chain of length l and mass m lies of the surface of a smooth hemisphere of radius R>l with one end tied to the top of the hemisphere. Taking base of the hemisphere as reference line, find the gravitational potential energy of the chain.
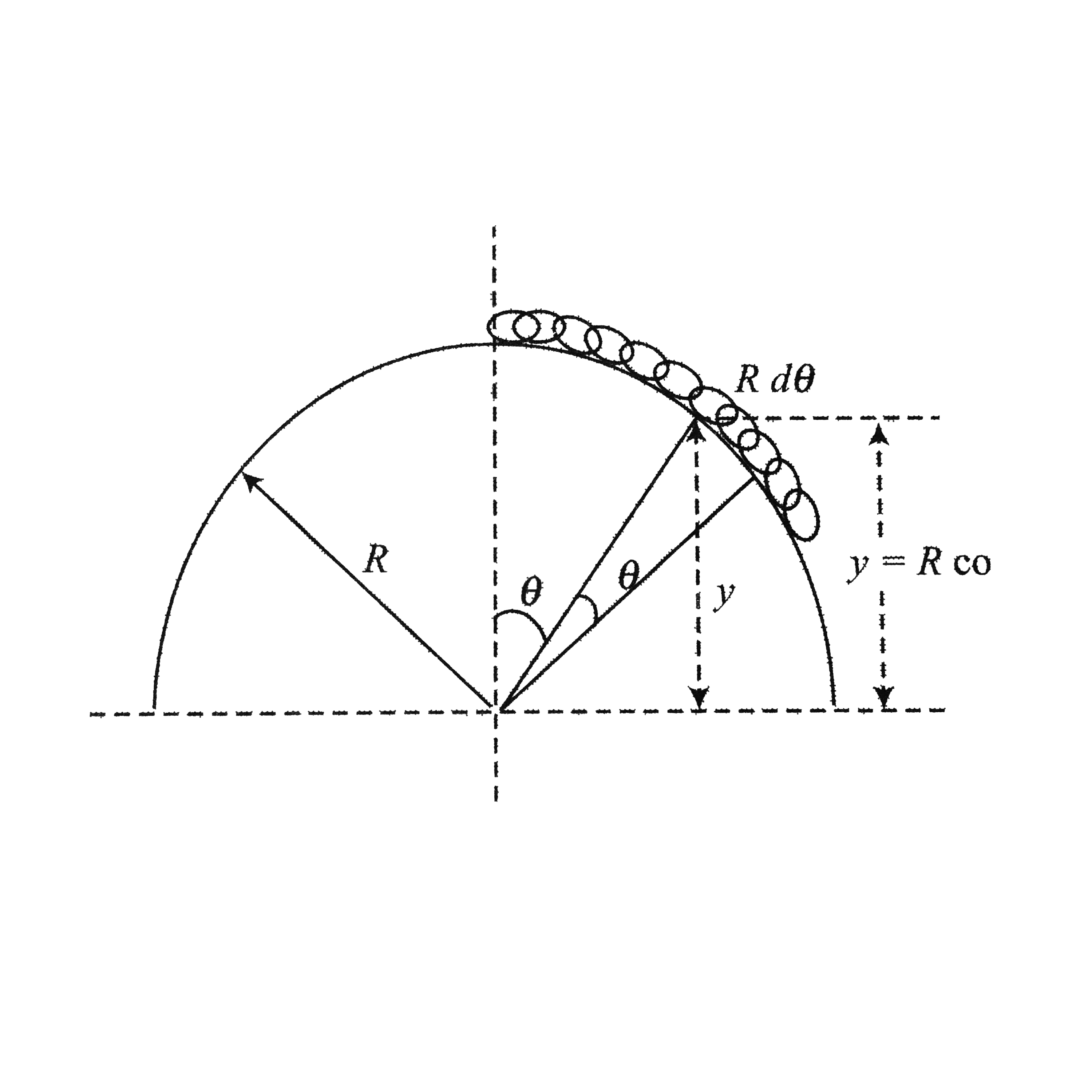
View SolutionAS chain of length l and mass m lies o the surface of a smooth sphere of radius R>l with one end tied to the top of the sphere. a.Find the gravitational potential energy of the chain with reference level at the centre of the sphere. B. suppose the chin is released and slides down the sphere. Find the kinetic eneergy of the chain, when it has slid through an angle θ c. find the tangential acceleration dvdt of the chain when the chain starts sliding down.
View SolutionA uniform chain of mass m and length l is placed on a smooth table so that one−third length hanges freely as shown in the figure. Now the chain is released, with what velocity chain slips off the table?

View SolutionA particle of mass m starts to slide down from the top of the fixed smooth sphere. What is the tangential acceleration when it break off the sphere ?
View SolutionA block of mass m is placed on a smooth sphere of radius R. It slides when pushed slightly. At what vertical distance h, from the top, will it leave the sphere?
View Solution
