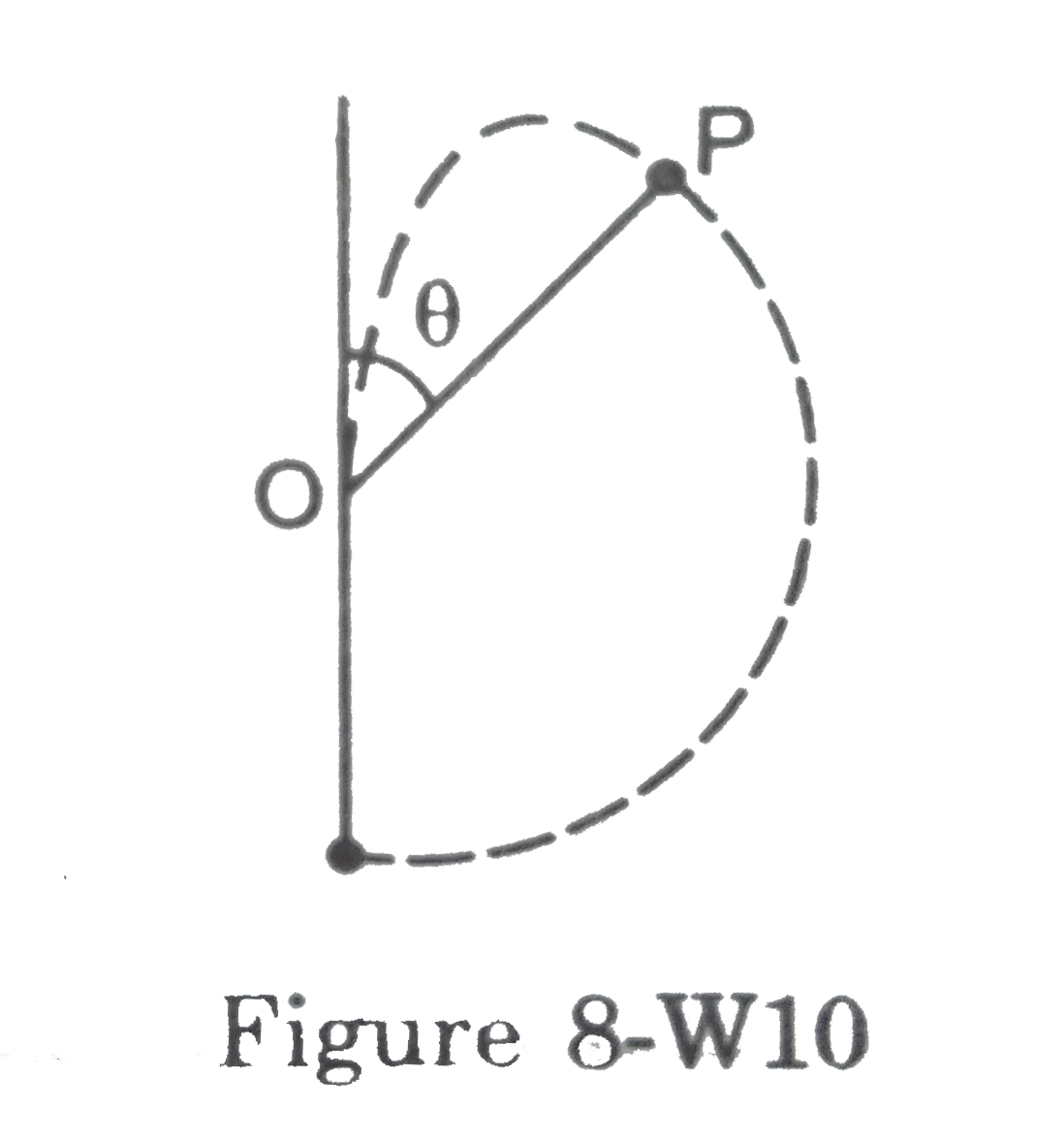
A small ball is hung as shown an a string of length L.
(a) If v0>√6gl, find the angle θ(<90∘) [in terms of, v0,g,L] with the upward vertical at which the string becomes slack.
(b) find the value of v0 [ in terms of g, L] if the particle passes through point of suspension
![A small ball is hung as shown an a string of length L. (a) If v(0) gt sqrt(6 g l), find the angle theta ( lt 90^(@)) [in terms of, v(0), g, L] with the upward vertical at which the string becomes slack. (b) find the value of v(0) [ in terms of g, L] if the particle passes through point of suspension](https://d10lpgp6xz60nq.cloudfront.net/physics_images/EAM_MEC_V01_C03_S01_041_Q01.png)
Step by step video & image solution for A small ball is hung as shown an a string of length L. (a) If v_(0) gt sqrt(6 g l), find the angle theta ( lt 90^(@)) [in terms of, v_(0), g, L] with the upward vertical at which the string becomes slack. (b) find the value of v_(0) [ in terms of g, L] if the particle passes through point of suspension by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- WORK AND ENERGYBook:ANURAG MISHRAChapter:WORK AND ENERGYExercise:Level 1
Explore 53 Videos
- WORK AND ENERGYBook:ANURAG MISHRAChapter:WORK AND ENERGYExercise:Level 2
Explore 18 Videos
- WORK AND ENERGYBook:ANURAG MISHRAChapter:WORK AND ENERGYExercise:Matching types problems
Explore 14 Videos
- UNIT AND DIMENSIONSBook:ANURAG MISHRAChapter:UNIT AND DIMENSIONSExercise:Matching Type Problem
Explore 4 Videos
Similar Questions
A heavy particle is suspended by a stirng of length l. The particle is given a horizontal velocity v0. The stirng becomes slack at some angle and the particle proceeds on a parabola.find the value of v0 if the prticle psses through the ponit of suspension
View SolutionIf l=0.90m,g=10ms2,find the value of √18.
View Solution
Knowledge Check
A mass m is hanging by a string of length l. The velocity v0 which must be imparted to it to just reach the top is
A√3glB√4glC√5glD√6glA particle of mass m suspended by a string of length l revolves in a horizontal circle (θ is the angle the string makes with vertical). Which of the following statement(s) is // are correct?
ATension in string =mgcosθBSpeed v of particle =√lgsin2θcosθCPeriod T=2π√lcosθgDCentripetal acceleration a=Fsinθm where F is tension

A ball is attached to a string of length L and the ball is given velocity v0 at its lowest point. Find the speed of the ball at point B,C and D. Assume that the ball is moving in vertical circle.
View SolutionTwo small balls A and B are interconnected by an inextensible string of legth L. Mass of ball A =m, mass of ball B = m. the balls are resting on a frictionlesss harixontal surgace , with the distance between them =3L.5 In this position ball A is suddenly given a harizontal velocity v0 perpendicular to the line joining the two balls. (see fig 4E . 18 (a))
(a) Find the speed of ball B houst after the string becomes taut
(b) find the impulse of the tension in string when the string becomes taut.
(c) Find the steady tension in string much after the string has become taut.

View SolutionIn example 1.49 find the velocity of the mid point of the rod in terms of its length l, v and θ.
View SolutionA bob of mass m is suspended by a light string of length L. It is imparted a horizontal velocity v0 at the lowest point A such that it completes a semi-circular trajectory in the vertical plane with the string becoming slack on reaching the topmost point C, figure, Obtain an expression for (i) v0 (ii) the speeds at points B and C, (ii) the ration of kinetic energies (KB/KC) at B and C.
Comment on the nature of the trajectory of the bob after it reahes the poing C.
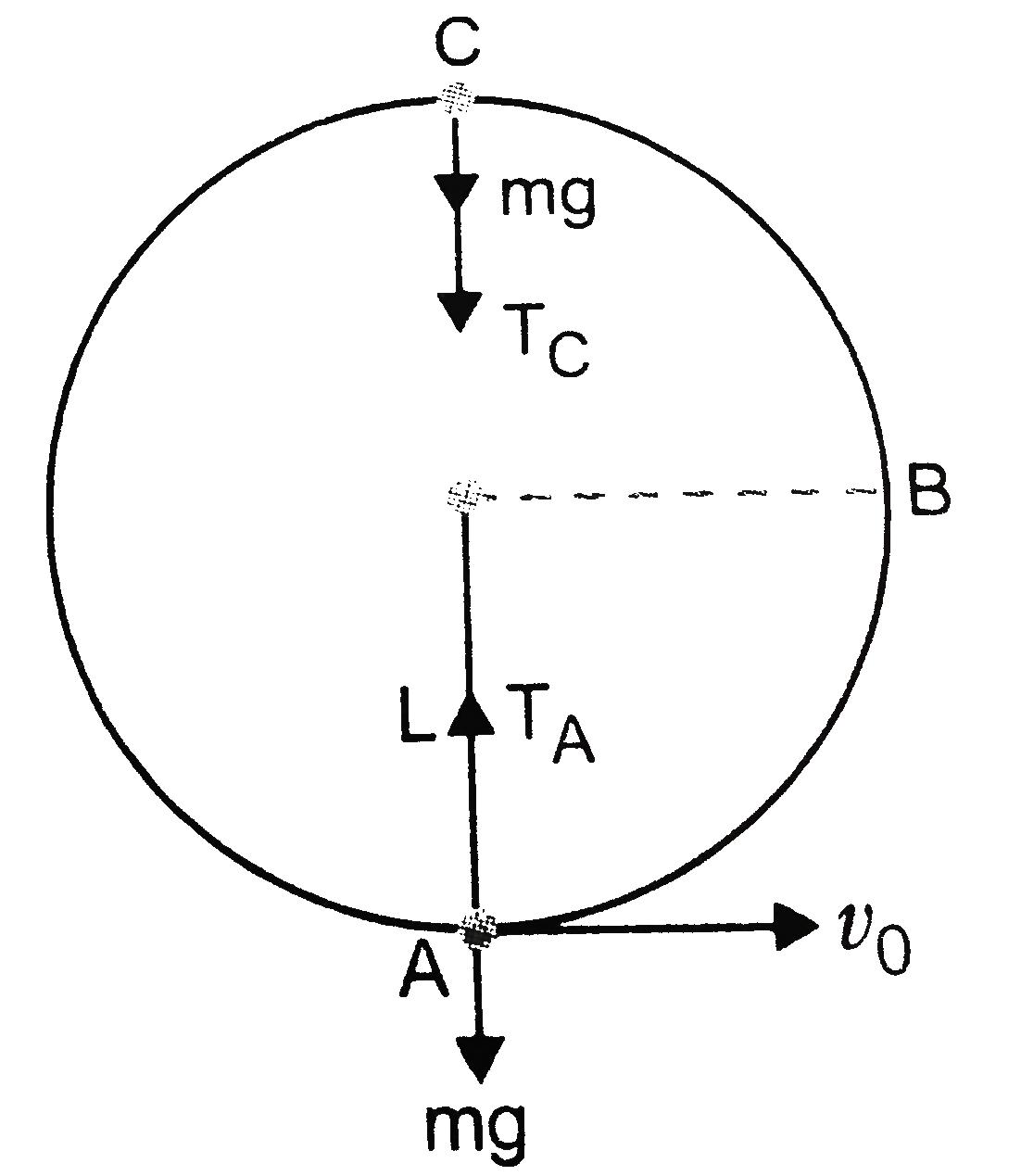
View Solution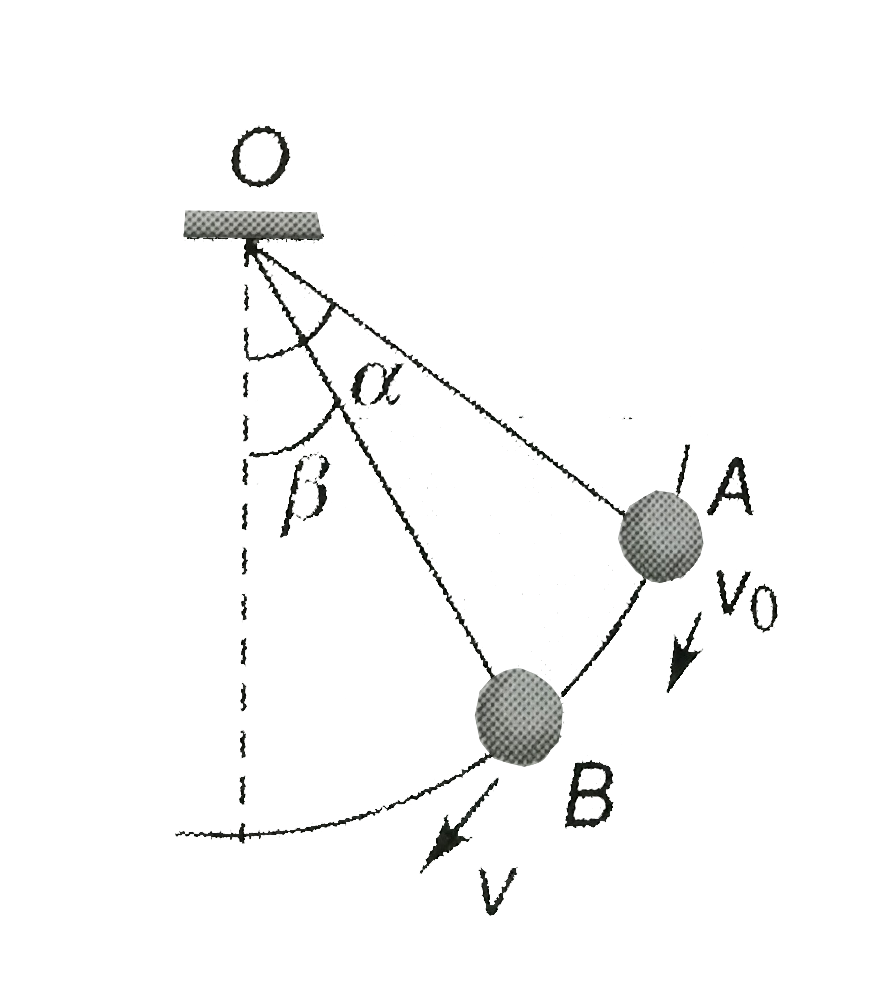
A ball attached to a string length L is oscillating line a simple pendulum. Find v in terms of v0 L α and β.
View SolutionA small ball of mass m is attached to a string of lengh R and moves in a vertical circle with a speed v m/s about a fixed point O as illustrated in fig. Find the tension in the string, when it makes an angle θ with the vertical, in terms of v,θ and g.
View Solution
