A uniform constant magnetic field B is directed at an angle of 45∘ to the xaξs in the xy- plane . PQRS is a rigid, square wire frame carrying a steady current I0, with its centre at the origin O. At time t=0, the frame is at rest in the position as shown in figure , with its sides parallel to the xandy axis. Each side of the frame is of mass M and length L.
(a) What is the torque τ about O acting on the frame due to the magnetic field?
(b) Find the angle by which the frame rotates under the action of this torque in a short interval of time Δt, and the axis about this rotation occurs .(Δtissoshorttˆanyvariation∈the→rquedur∈gthis∫ervalmaybe¬≤cted.)Given:themomentof∫eriaoftheameaboutanaξsthroughitscentreperpendica––r→itsaboutanaξsthroughitscentreperpendica––r→itspla≠is(4)/(3) ML^(2).
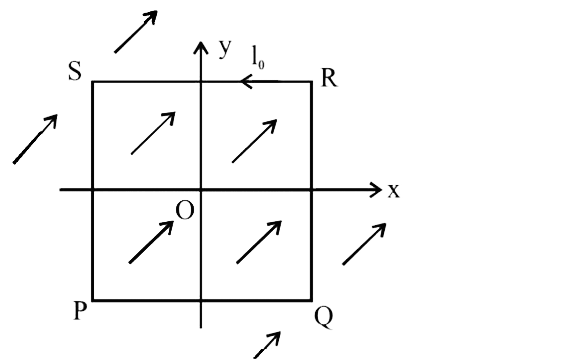
(a) As magnetic field is in x-y plane and subtended an angle of
45∘ with x-axis,
Bx=Bcos45∘=B/√2
and BY=Bsin45∘=B/√2
so, in vector form →B=ˆi(B/√2)+ˆj(B/√2)
and →M=I0Sˆk=I0L2ˆk
⇒→τ=→M×→B=I0L2ˆk×(B√2ˆi+B√2ˆj)
⇒→τ=I0L2B√2×(−ˆi+ˆj)
i.e,torque has magnitude I0L2B and
is directed along the line QS from
Q to S.

(b) By the theoram of perpendicular
axis, moment of inertia of the frame
about QS,
IQS=12Iz=12(43ML2)=23ML2
as τ=Iα⇒ατI=I0L2B×32L2M=32I0BM
As here α is constant, equation of circular motion are
valid. Hence, from θ=ω0t+12αt2, with ω0=0, we have
θ=12αt2=12(32I0BM)(Δt)2=34I0BMΔt2
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Exercise 1.122videos
MAGNETIC FIELD AND MAGNETIC FORCES
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Exercise 1.213videos
MAGNETIC FIELD AND MAGNETIC FORCES
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Multiple Correct Answer type2videos
MAGNETIC FIELD AND MAGNETIC FORCES
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Concept Based8videos
INDUCTANCE
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - True and False3videos
MISCELLANEOUS VOLUME 3
Similar Questions
A uniform electric field of 400V/m is directed at 45∘ to the positive X-axis, in the X−Y plane as shown in figure
 View Solution
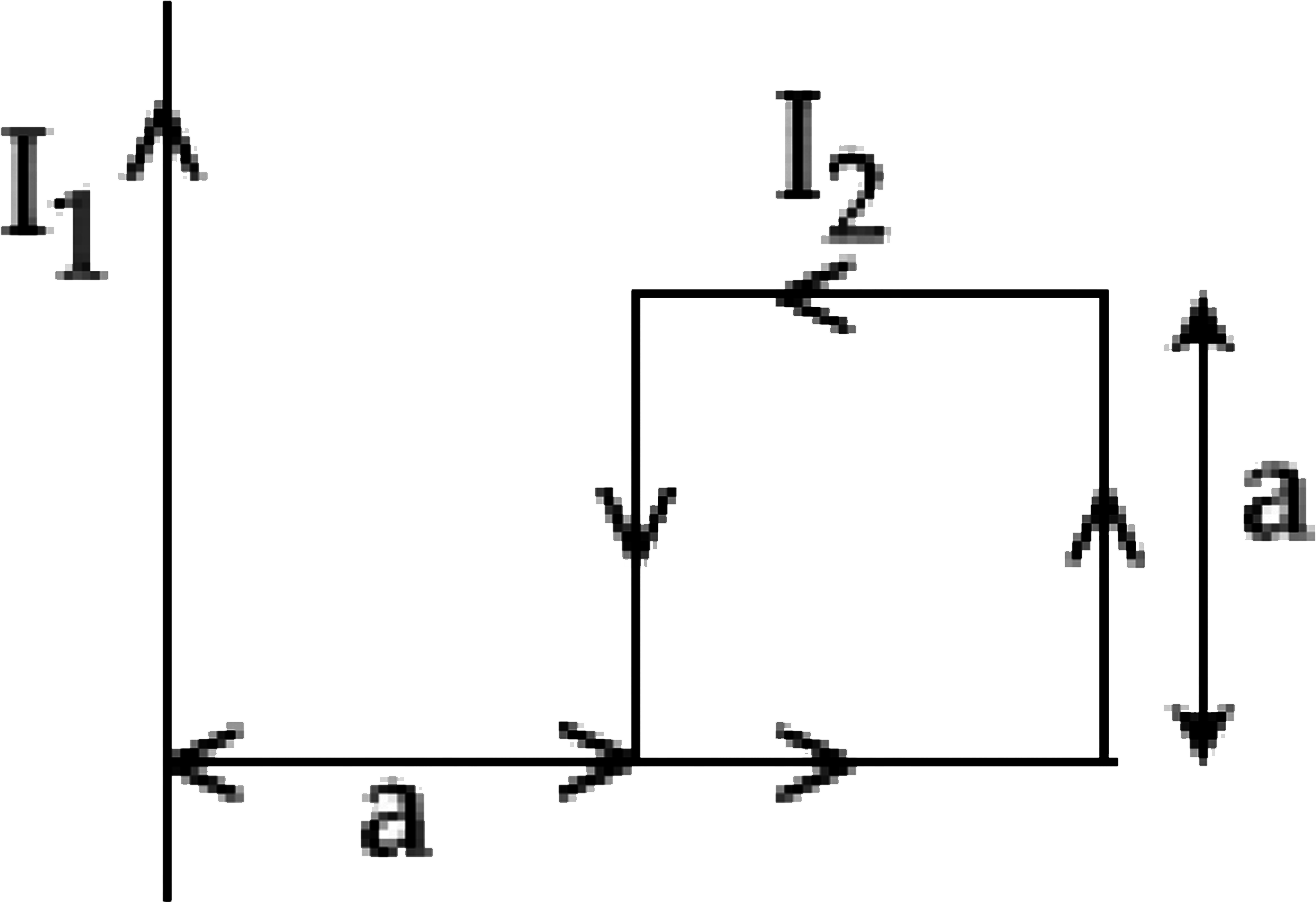
View SolutionA rigid square loop of side 'a' and carrying current I2 is lying on a horizontal surface near a long current I1 carrying wire in the same plane as shown in figure. The net force on the loop to the wire will be :
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Current flows through uniform square frames as shown. In which case is the magnetic field at the centre of the frame not zero ?
A B
B C
C D
D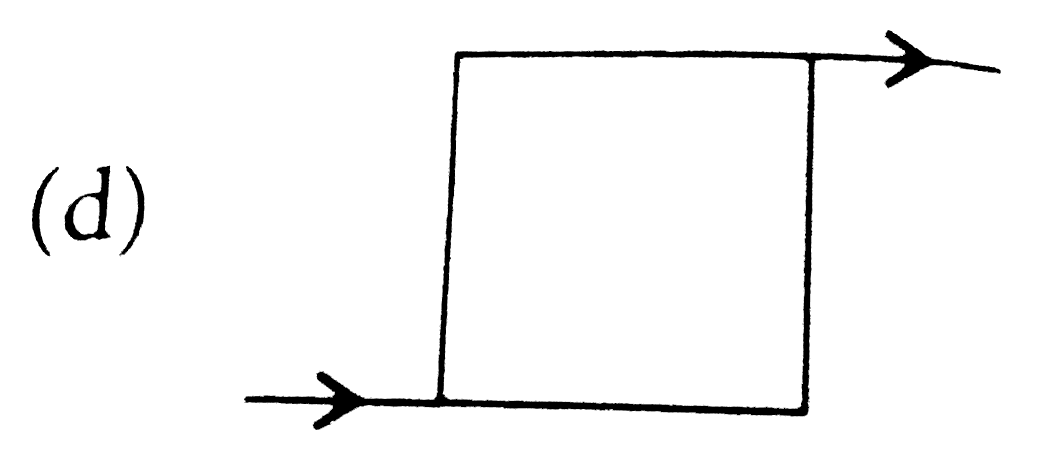
- Question 2 - Select One
Current flows through uniform square frames as shown. In which case is the magnetic field at the centre of the frame not zero ?
A B
B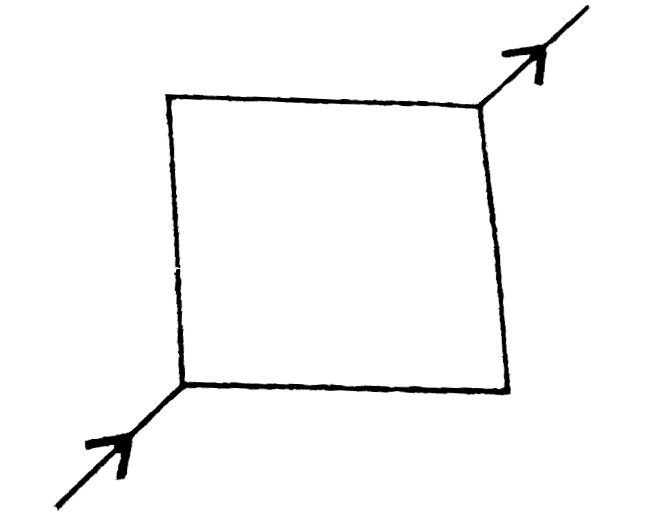 C
C D
D
A square loop of side a carris a current I. The magnetic field at the centre of the loop is
View SolutionFour identical rods each of mass m and length l are joined to form a rigid square frame. The frame lies in the xy plane, with its centre at the origin and the sides parallel to the x and y axes. Its moment of inertia about
View SolutionA rectangular loop carrying a current i2 situated near a long straight wire carrying a steady current i1. The wire is parallel to one of the sides of the loop and is in the plane of the loop as shown in the figure. Then the current loop will
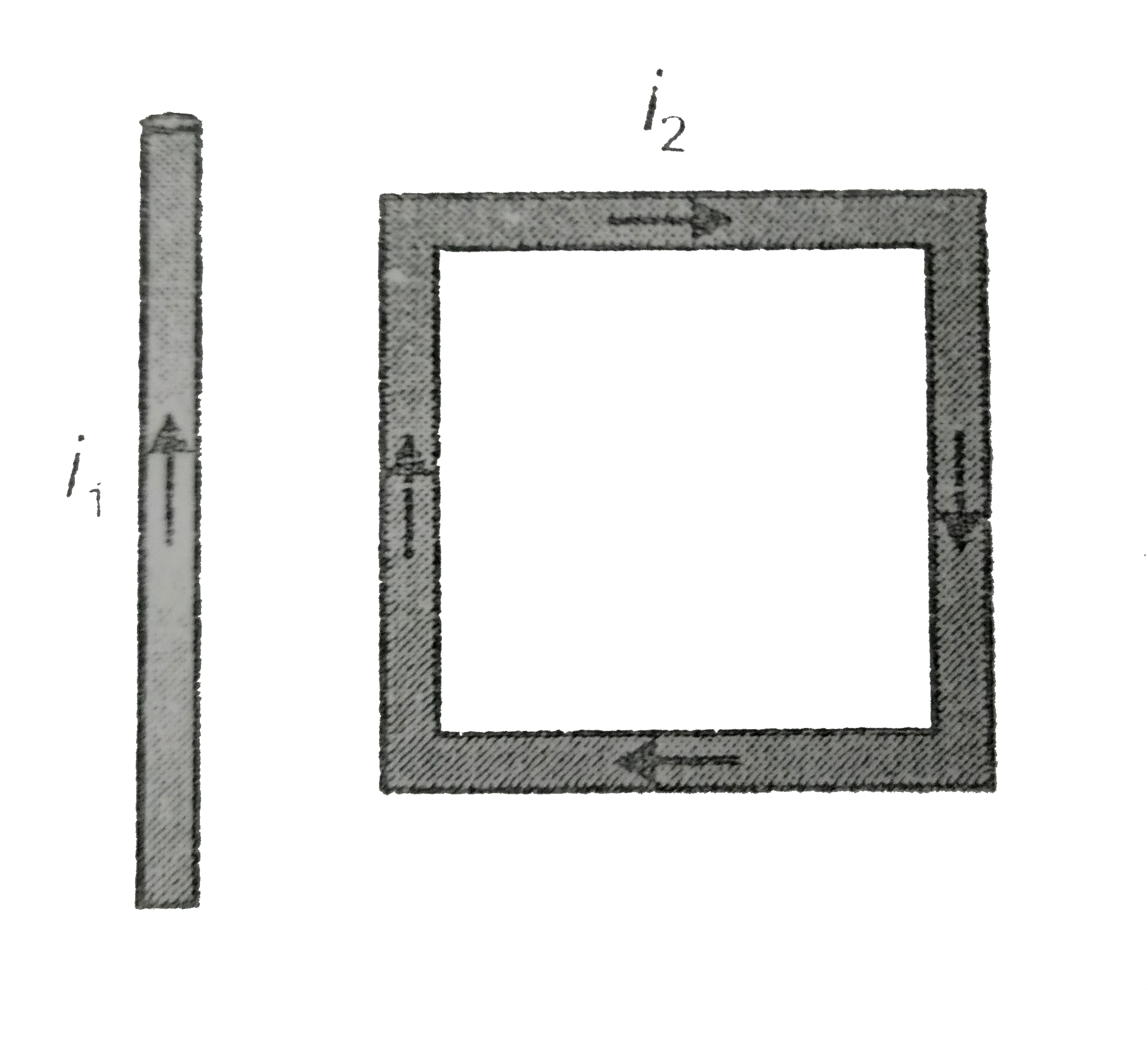 View Solution
View SolutionAn equilateral triangle frame PQR of mass M and side a is kept under the influence of magnetic force due to inward perpendicular masgnetic fidl B and gravitational field as shownin the figure. Te magnitude and direction of current in the frame so that the frame remains at rest is
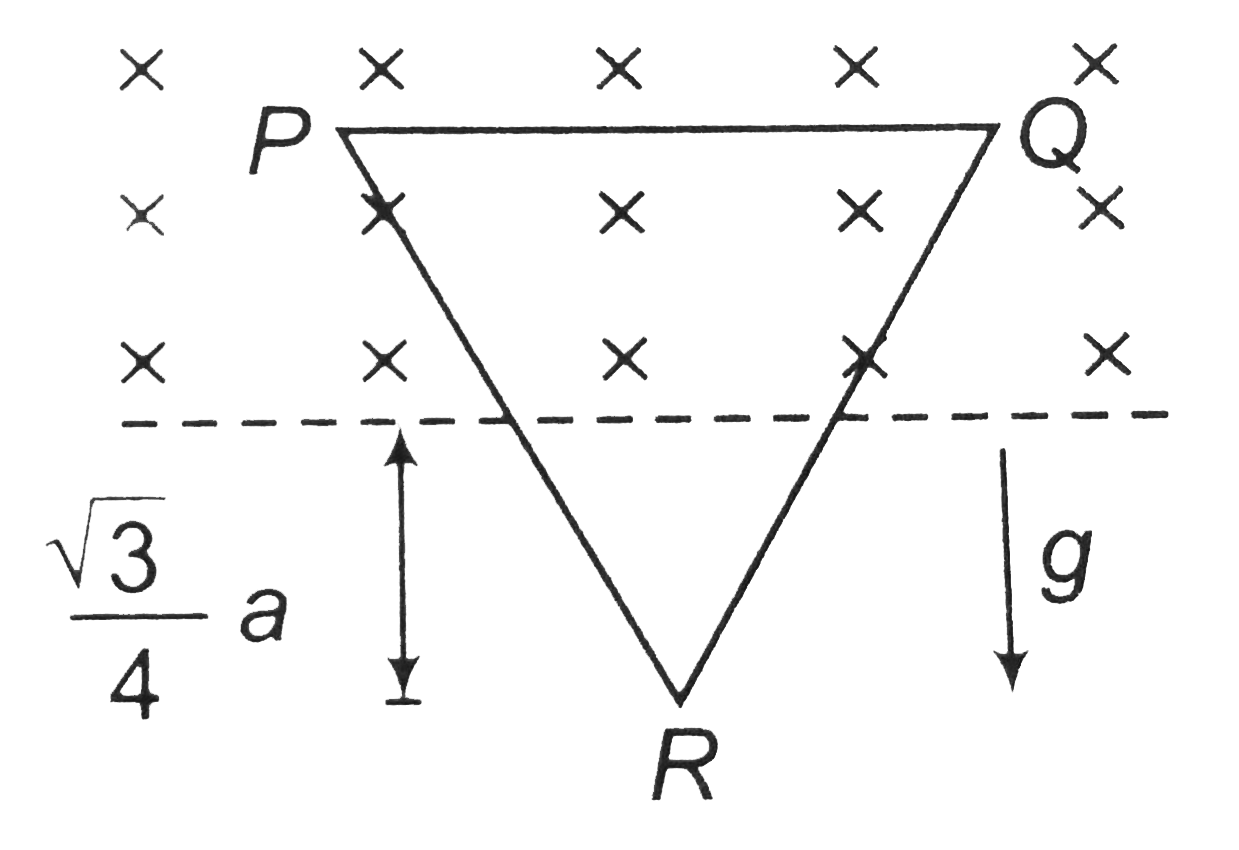 View Solution
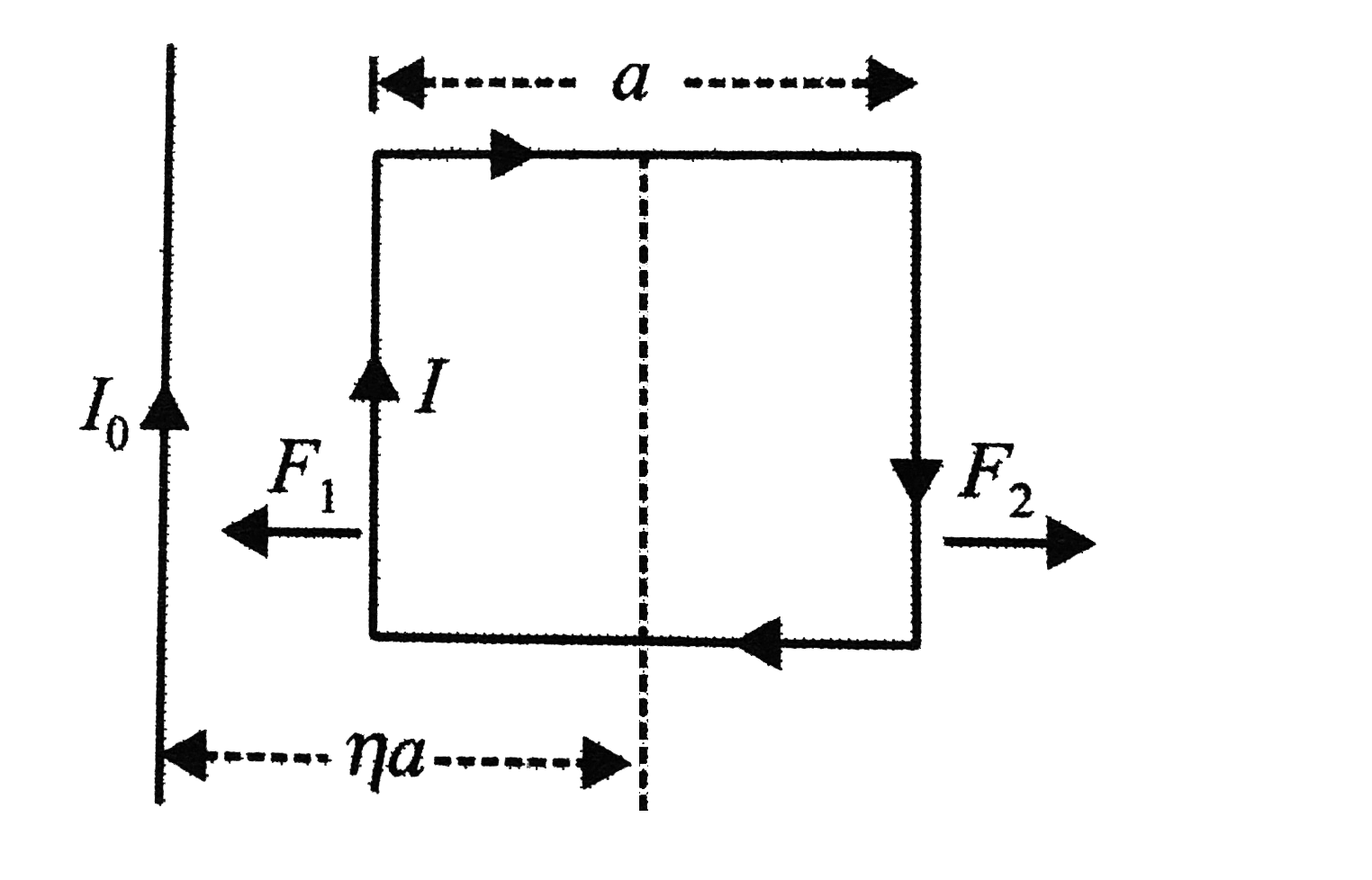
View SolutionA square frame carrying a current I=0.90A is located in the same plane as a long straight wire carrying a current I0=5A, The frame side has a length a=8cm. The axis of the frame passing through the mid-point of the opposite sides is parrallel to the wire and is separated form it by a distance h=15 times greater tahn the side of the frame.
Find:
(a) ampere force acting on the frame.
(b) The machanical work to be performed in order to turn the frmae through 180∘ about its axis, with the current maintained constant.
 View Solution
View SolutionA wire frame of given shape, carrying current of 10 A is placed in uniform magnetic field 100 T directed into the plane of paper as shown in figure. The net force acting on frame is
View Solution
