A wire frame of given shape, carrying current of 10 A is placed in uniform magnetic field 100 T directed into the plane of paper as shown in figure. The net force acting on frame is
100ˆjN
100
67.5ˆjN
67.5ˆ−jN
To solve the problem of finding the net force acting on a wire frame carrying a current in a magnetic field, we can follow these steps:
1. Identify the Given Values:
- Current (I) = 10 A
- Magnetic Field (B) = 100 T
- The shape of the wire frame is a triangle with dimensions:
- Base = 4 cm
- Height = 3 cm
- Hypotenuse = 5 cm
- Convert dimensions to meters:
- Base = 0.04 m
- Height = 0.03 m
- Hypotenuse = 0.05 m
2. Calculate the Total Length of the Wire Frame:
- The wire frame consists of three sides: two bases (4 cm each) and one hypotenuse (2 cm).
- Total Length (L) = Base + Base + Hypotenuse = 0.04 m + 0.04 m + 0.02 m = 0.10 m
3. Use the Formula for Magnetic Force:
- The force (F) acting on a current-carrying conductor in a magnetic field is given by the formula:
F=B⋅I⋅L
- Substitute the known values into the formula:
F=100T⋅10A⋅0.10m
4. Calculate the Force:
- Calculate:
F=100⋅10⋅0.10=100N
5. Determine the Direction of the Force:
- Using the left-hand rule, the direction of the force can be determined. Since the magnetic field is directed into the plane of the paper, and the current is flowing in a specific direction, the force will act upwards (in the positive y-direction).
6. Final Result:
- Therefore, the net force acting on the frame is:
Net Force=100N^j
Conclusion:
The net force acting on the wire frame is 100^jN.
- Current (I) = 10 A
- Magnetic Field (B) = 100 T
- The shape of the wire frame is a triangle with dimensions:
- Base = 4 cm
- Height = 3 cm
- Hypotenuse = 5 cm
- Convert dimensions to meters:
- Base = 0.04 m
- Height = 0.03 m
- Hypotenuse = 0.05 m
- The wire frame consists of three sides: two bases (4 cm each) and one hypotenuse (2 cm).
- Total Length (L) = Base + Base + Hypotenuse = 0.04 m + 0.04 m + 0.02 m = 0.10 m
- The force (F) acting on a current-carrying conductor in a magnetic field is given by the formula:
F=B⋅I⋅L
- Substitute the known values into the formula:
F=100T⋅10A⋅0.10m
- Calculate:
F=100⋅10⋅0.10=100N
- Using the left-hand rule, the direction of the force can be determined. Since the magnetic field is directed into the plane of the paper, and the current is flowing in a specific direction, the force will act upwards (in the positive y-direction).
- Therefore, the net force acting on the frame is:
Net Force=100N^j
The net force acting on the wire frame is 100^jN.
Topper's Solved these Questions
Similar Questions
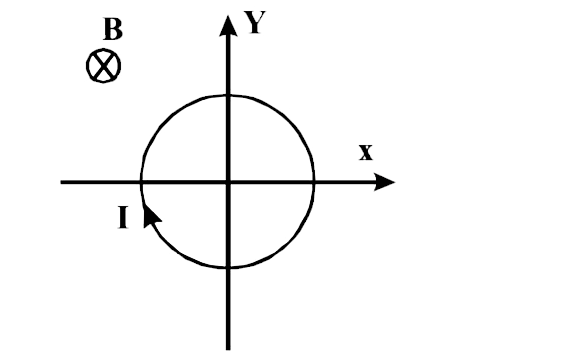
A conducting loop carrying a current I is placed in a uniform magnetic field ponting into the plane of the paper as shown. The loop will have a tendency to
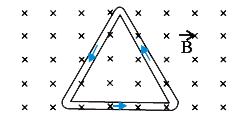
View SolutionA wire is bent in the form of an equilateral triangle of side 1m and carries a current of 2A.. It is placed in a magnetic field of induction 2.0 T directed into the plane of paper. The direction and magnitude of magnetic force acting on each side of the triangle will be
View SolutionA non planar closed loop of arbitrary shape carryign a current I is placed in uniform magnetic field. The force acting on the loop
View SolutionLet current i=2A be flowing in each part of a wire frame as shown in Fig. 1.138. The frame is a combination of two equilateral triangles ACD and CDE of side 1 m. It is placed in uniform magnetic field B=4T acting perpendicular to the plane of frame. The magnitude of magnetic force acting on the frame is
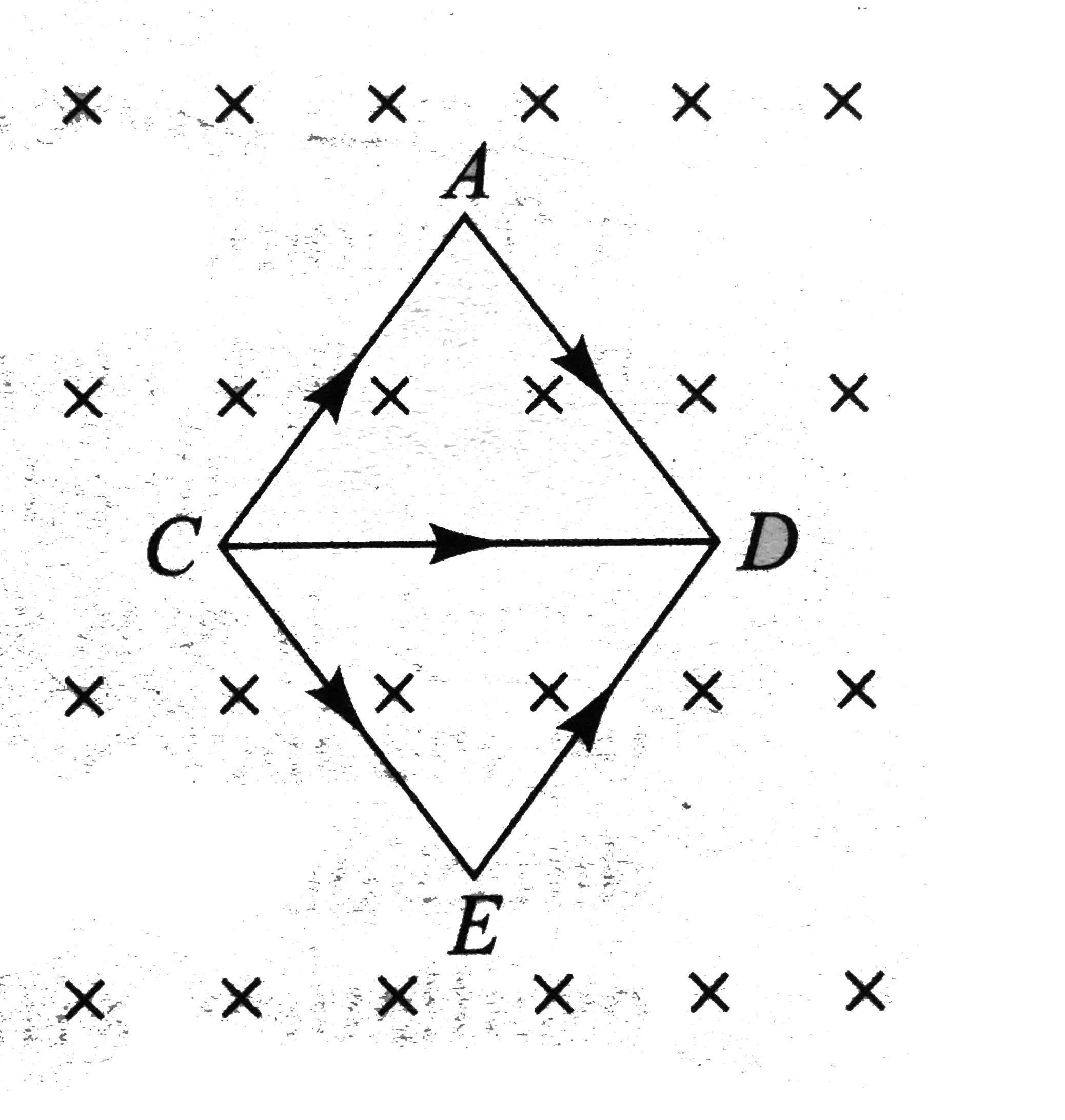
View SolutionSame current i=2 A is flowing in a wire frame as shown in the figure. The frame is a combination of two equilateral triangles ACD and CDE of side 1 m. It is placed in uniform magnetic field B=4 Tacting perpendicular to the plane of frame. The magnitude of magnetic force acting on the frame is

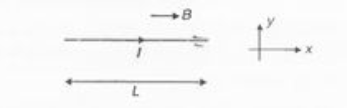
View Solutionthe force on current carrying wire placed in uniform magnetic field B as shown in figure is
View SolutionLet current i=2A be flowing in each part of a wire frame as shown in Fig. 1.138. The frame is a combination of two equilateral triangles ACD and CDE of side 1 m. It is placed in uniform magnetic field B=4T acting perpendicular to the plane of frame. The magnitude of magnetic force acting on the frame is
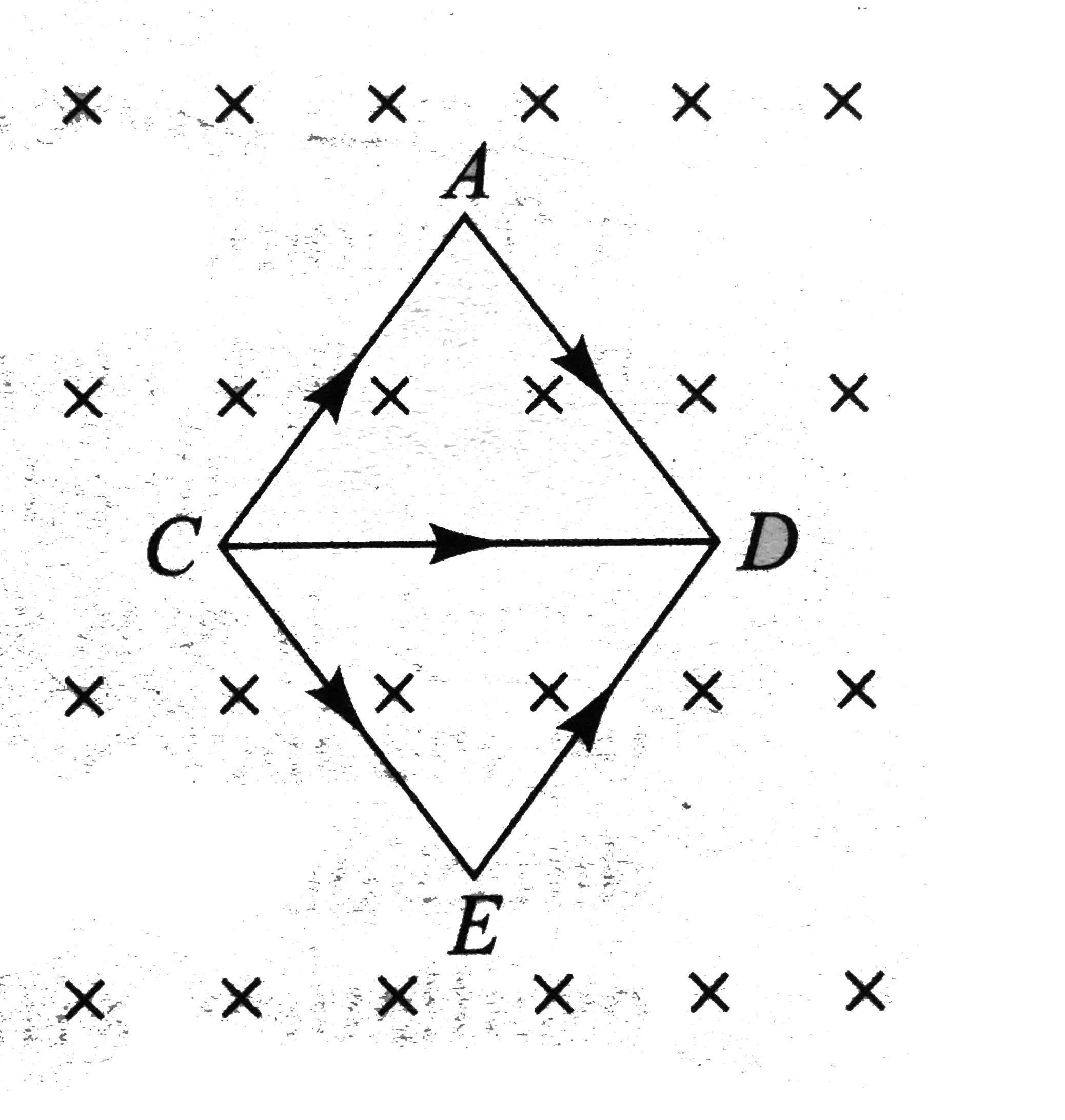
The pithc of the helical path followed by the particle is p. The radius of the helix will be
View SolutionLet current i=2A be flowing in each part of a wire frame as shown in Fig. 1.138. The frame is a combination of two equilateral triangles ACD and CDE of side 1 m. It is placed in uniform magnetic field B=4T acting perpendicular to the plane of frame. The magnitude of magnetic force acting on the frame is
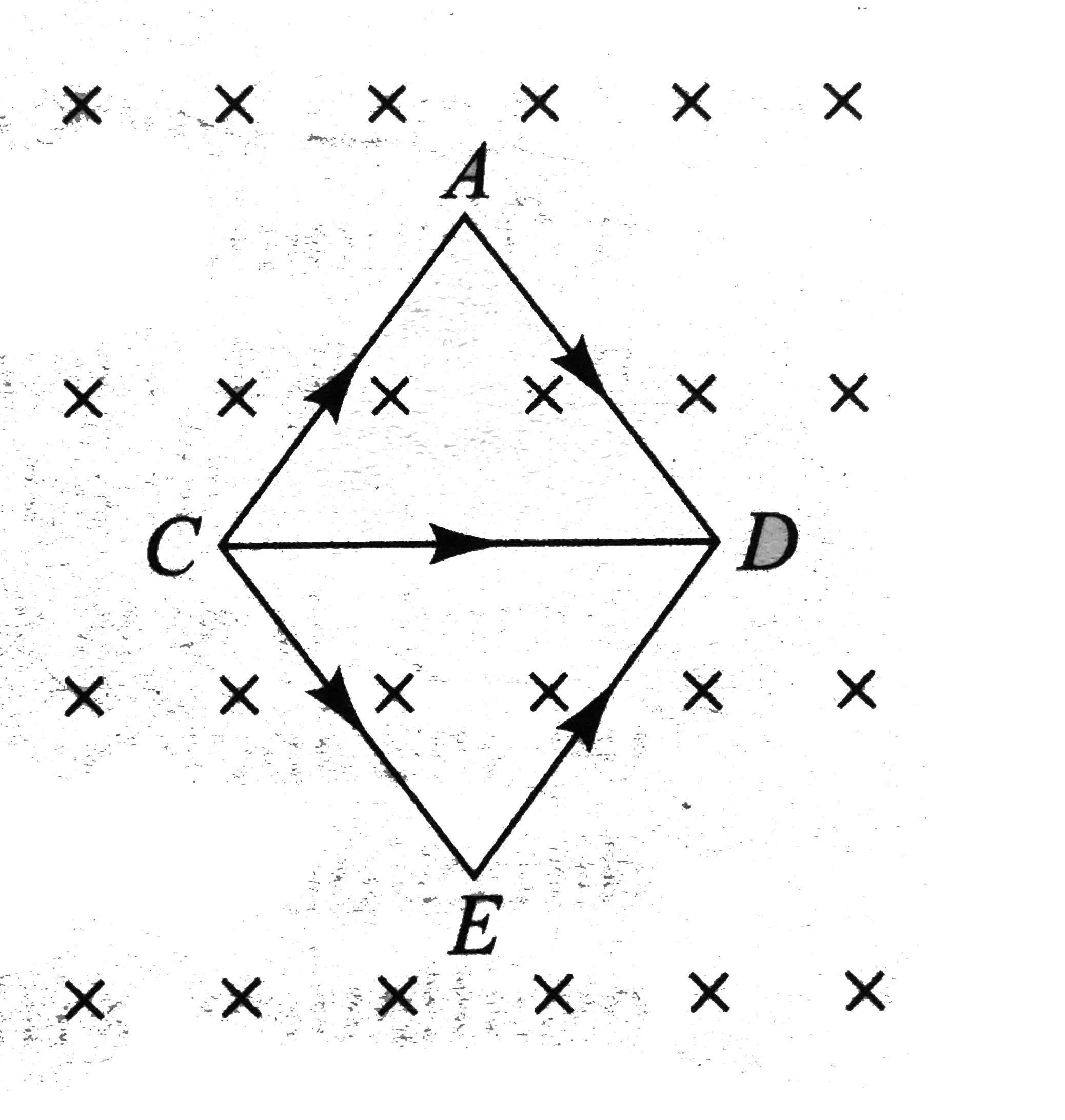
The pithc of the helical path followed by the particle is p. The radius of the helix will be
View SolutionA current carrying circular loop of radius R is placed in a uniform magnetic field B0 Tesla in x-y plane as shown in figure. The loop carries a current i=1A in the direction shown. Find the torqure acting on the loop
View SolutionFigure shows an equilateral triangle ABC of side l carrying currents as shown, and placed in a uniform magnetic field B perpendicular to the plane of triangle. The magnitude of magnetic force on the triangle is

View Solution
