A uniform cylinder of mass m, length l and cross sectional area A is suspended with its vertical from a fixed point, with the help of a massless spirng of force constant (K), The cylinder is then submerged in a liquid of density p. At equilibrium the cylinder remains submerged in the liquid with 1/4th of its volume outside the liquid, as shown in the figure. The elongation of hte spring at this point is x0. WHen the cylinder is given a slight downward push into the liquid and then released, its starts oscillating with vertical S.H.M. of small amplitude.

If the cyleinder is displced by a small downward displacement a from its equilibrium postion and then released , the restoring force on it will be
−[K+Apg]a4
−[K+14Apg]a
−[K−14Apg]a
−[K+Apg]a
The correct Answer is:D
When a small downward displacement a is given to the cyliner, then the submerged length of the cylinder becomes (3l/4 + a). So, the extension produced in the spring is now (x0+a). The upthrust acting on the cylinder will become
U.=(3l4+a)Aρg
Force in the spring =k(x0+a)
So, the restoring force on the cylinder is
F=−[k(x0+a)−{mg−(3l4+a)}Aρg]...(ii)
Using (i) and (ii), we get
F=−[k+Aρg]a
Topper's Solved these Questions
- OSCILLATIONS BOOK - MODERN PUBLICATIONCHAPTER - OSCILLATIONS EXERCISE - Competition File (Matching Type Questions)
2 Videos
- OSCILLATIONS BOOK - MODERN PUBLICATIONCHAPTER - OSCILLATIONS EXERCISE - Competition File (MATRIX MATCH TYPE QUESTIONS)
2 Videos
- OSCILLATIONS BOOK - MODERN PUBLICATIONCHAPTER - OSCILLATIONS EXERCISE - Competition File (Multiple choice question)
11 Videos
- MOTION IN A STRAIGHT LINE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - CHAPTER PRACTICE TEST
16 Videos
- PHYSICAL WORLD BOOK - MODERN PUBLICATIONCHAPTER - PHYSICAL WORLD EXERCISE - Revision exercises (Long answer questions)
6 Videos
Similar Questions

View SolutionColumn I describes some situations in which a small object moves. Column II describes some characteristics of these motion. Match the situtions in column I with the characteristics in column II.

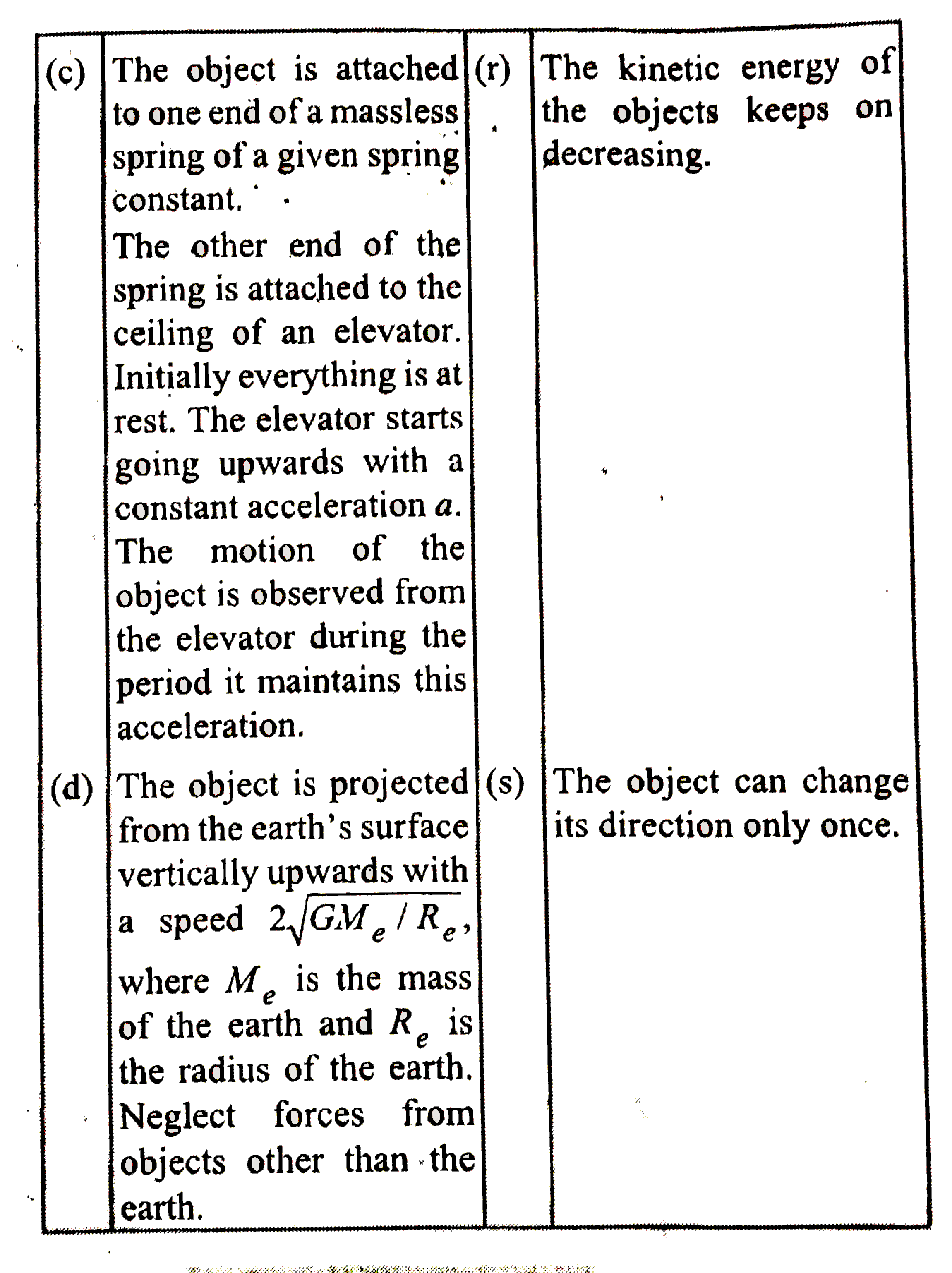
View SolutionIf the function x=cos2ωt+bsin2ωt+csinωtcosωt represent a simple harmonic motion , then which of the foloowing options can be possible ?
View SolutionWhen can say that circular motion is periodic ?
View SolutionWhat are the main features of gravitational force?
View SolutionA uniform cylinder of length L and mass M having cross-sectional area A is suspended, with its length vertical, from a fixed point by a massless spring such that it is half submerged in a liquid of density sigma at equilibrium position. The extension x_0 of the spring when it is in equlibrium is:
View SolutionA uniform cylinder of length (L) and mass (M) having cross sectional area (A) is suspended, with its length vertical, from a fixed point by a massless spring, such that it is half - submerged in a liquid of density (rho) at equilibrium position. When the cylinder is given a small downward push and released it starts oscillating vertically with small amplitude. If the force constant of the spring is (k), the prequency of oscillation of the cylindcer is.
View SolutionA wooden cylinder of length l floats vertically in a liquid of specific gravity rho with ((1)/(3))^(rd) part of its length submerged. Another liquid that is immiscible with the previous liquid is poured into it, to just completely submerge the cylinder. If the density of the liquid at the bottom, density of cylinder and density of upper liquid are in G.P., find the fraction of the cylinder submerged in lower liquid.
View SolutionA uniform cylinder of length L and mass M having cross sectional area A is suspended , with its length vertical, from a fixed point by a massless spring of spring constant k,such that it is half submerged in a liquid of density sigma at equilibrium position. What is the extension of the spring when it is in equilibrium?
View SolutionA uniform cylinder of length L and mass M having crosssectional area A is suspended, with its length vertical, from a fixed point by a massless spring, such that it is half submerged in a liquid of density σ at equilibrium position. The extension x0 of the spring when it is in equilibrium is :
View SolutionA uniform cylinder of height h, mass m and cross sectional area A is suspended vertically from a fixed point by a massless spring of force constant k, A beaker full of water is placed under the cylinder so that 1//4^(th) of its volume is submerged in the water at equilibrium position. When the cylinder is given a small downward push and released, it starts oscillating vertically with small amplitude. Calculate the frequency of oscillation of the cylinder, Take, density of water = rho .
View SolutionA uniform cylinder of mass m, length l and cross sectional area A is suspended with its vertical from a fixed point, with the help of a massless spirng of force constant (K), The cylinder is then submerged in a liquid of density p. At equilibrium the cylinder remains submerged in the liquid with 1/4th of its volume outside the liquid, as shown in the figure. The elongation of hte spring at this point is x0. WHen the cylinder is given a slight downward push into the liquid and then released, its starts oscillating with vertical S.H.M. of small amplitude.

The elongation X0 produced in the springs when the syste is in equilibrium is
View SolutionA uniform cylinder of mass m, length l and cross sectional area A is suspended with its vertical from a fixed point, with the help of a massless spirng of force constant (K), The cylinder is then submerged in a liquid of density p. At equilibrium the cylinder remains submerged in the liquid with 1//4^(th) of its volume outside the liquid, as shown in the figure. The elongation of hte spring at this point is x_(0) . WHen the cylinder is given a slight downward push into the liquid and then released, its starts oscillating with vertical S.H.M. of small amplitude. Time period of vertical S.H.M of the cylinder is
View SolutionA uniform cylinder of length L and mass M having cross-sectional area A is suspended, with its length vertical, from a fixed point by a massless spring, such that it is half submerged in a liquid of density sigma at equilibrium position. When the cylinder is given a downward push and released, it starts oscillating vertically with a small amplitude. The time period T of the oscillations of the cylinder will be :
View SolutionA uniform cylinder of length L and mass M having cross-sectional area A is suspended, with its length vertical, from a fixed point by a massless spring such that it is half submerged in a liquid of density sigma at equilibrium position. The extension x_0 of the spring when it is in equlibrium is:
View Solution
