A uniform cylinder of mass m lies on a fixed plane inclined at a angle θ with the horizontal. A light string is tied to the cylinder at the rightmost point, and a mass m hangs from the string as shown. Assume that the coefficient of friction between the cylinder and the incline plane is sufficiently large to prevent slipping. for the cylinder to remain static the value of m is

Msinθ1−sinθ
Mcosθ1+sinθ
Msinθ1+sinθ
Mcosθ1−sinθ
The correct Answer is:A
T=mg
f=mgsinθ+Tsinθ
⇒f=Mgsinθ+mgsinθ
balancing torque about C

Tr=fr
⇒mg=Mgsinθ+mgsinθ
⇒m=Msinθ1−sinθ
Topper's Solved these Questions
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Multiple Correct
9 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Linked Comprehension
28 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Subjective
13 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE
2 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Interger
2 Videos
Similar Questions
A solid cylinder of mass M and radius R rolls from rest down a plane inclined at an angle θ to the horizontal. The velocity of the centre of mass of the cylinder after it has rolled down a distance d is :
View SolutionA horizontal uniform rod of mass 'm' has its left end hinged to the fixed incline plane, while its right end rrests on the top of a uniform cylinder of mass 'm' which in turn is at rest on the fixed inclined plane as shown. The coefficient of friction between the cylinder and rod, and between the cylinder and inclined plane, is sufficient to keep the cylinder at rest.
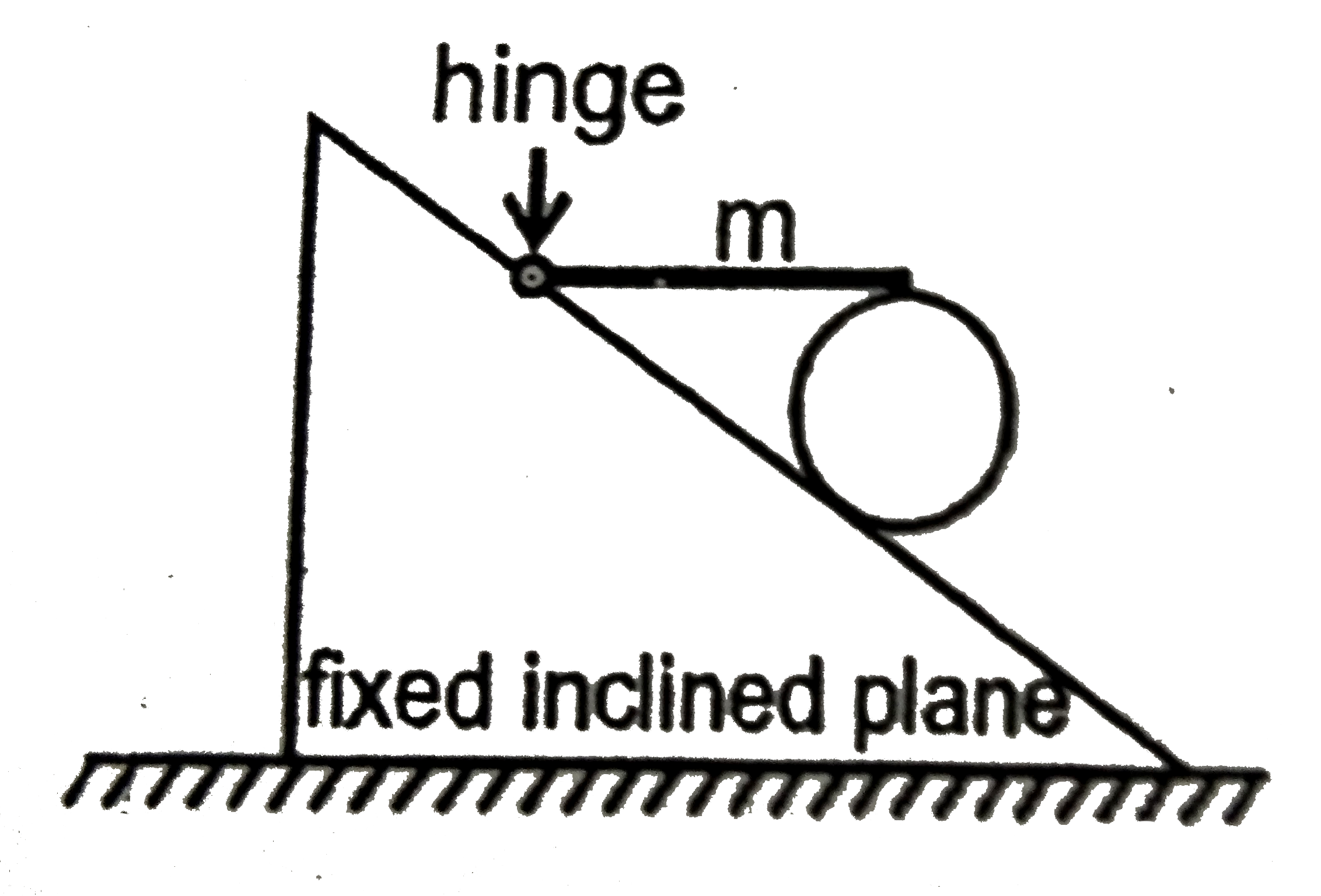
The ratio of magnitude of frictional force on the cylinder due to the rod and the magnitude of frictional force on the cylinder due to the inclined plane is :
View Solution
Knowledge Check
A solid cylinder of mass M and radius R rolls without slipping down an inclined plane making an angle 6 with the horizontal. Then its acceleration is.
A1/3 g sinθB2/3 g sinθC2/5 g sinθD2/7 g sinθA cylinder of radius R and mass M rolls without slipping down a plane inclined at an angle θ. Coeff. of friction between the cylinder and the plane is μ. For what maximum inclination θ, the cylinder rolls without slipping ?
Atanθ gt 3μsBtanθ ≤ 3μsCtanθ lt 3μsDNone of these
A horizontal uniform rod of mass 'm' has its left end hinged to the fixed incline plane, while its right end rrests on the top of a uniform cylinder of mass 'm' which in turn is at rest on the fixed inclined plane as shown. The coefficient of friction between the cylinder and rod, and between the cylinder and inclined plane, is sufficient to keep the cylinder at rest.

The magnitude of normal reaction exerted by the inclinded plane on the cylinder is :
View SolutionA horizontal uniform rod of mass 'm' has its left end hinged to the fixed incline plane, while its right end rrests on the top of a uniform cylinder of mass 'm' which in turn is at rest on the fixed inclined plane as shown. The coefficient of friction between the cylinder and rod, and between the cylinder and inclined plane, is sufficient to keep the cylinder at rest.
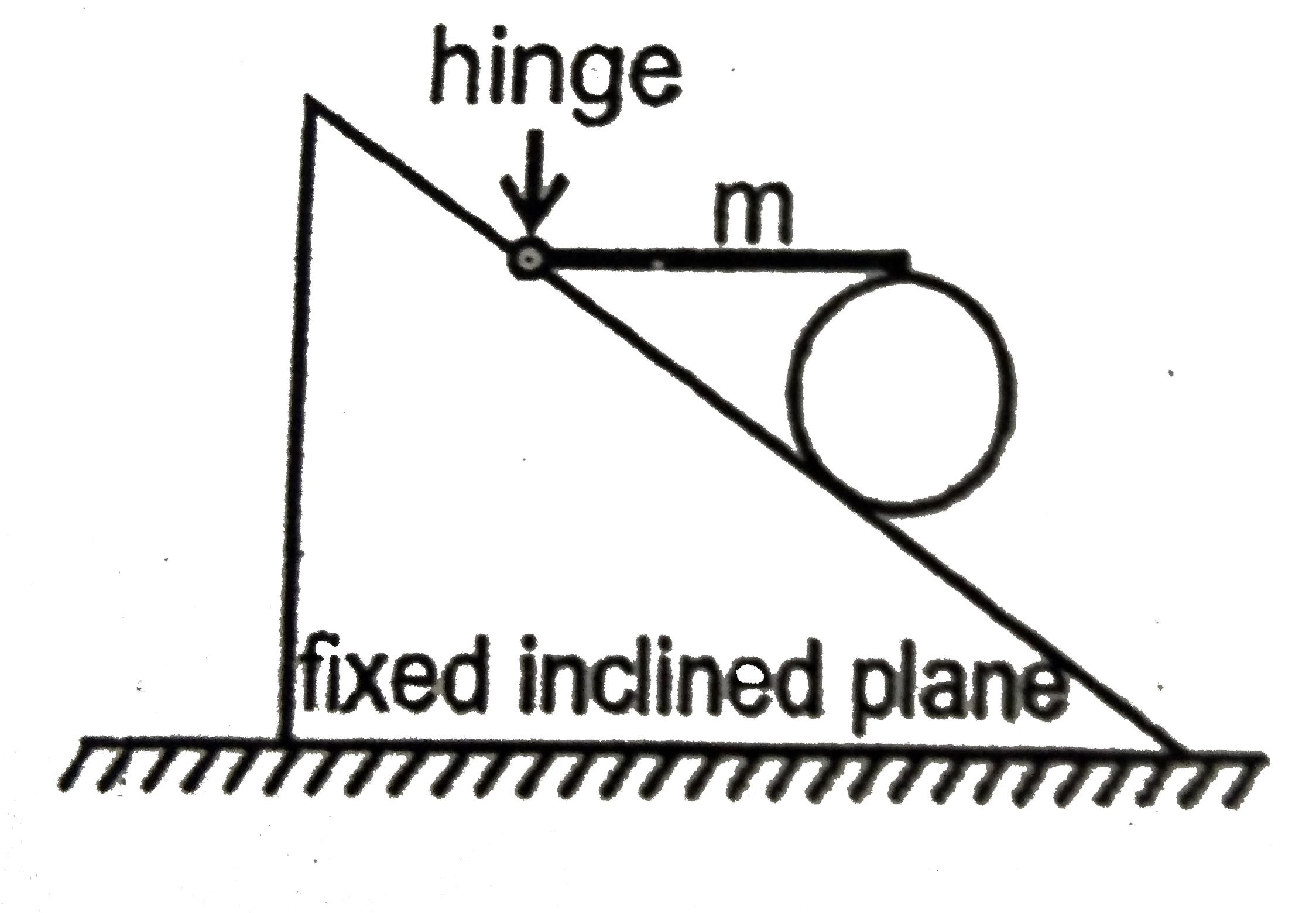
The magnitude of normal reaction exerted by the rod on the cylinder is
View SolutionA solid cylinder is rolling down on an inclined plane of angle θ. The minimum value of the coefficient of friction between the plane and the cylinder to allow pure rolling
View SolutionA cylinder is released from the top of an incline making angle θ=45∘ with the horizontal. The length of the incline is 2.82m and mass of cylinder is 1kg. The coefficient of friciton is 0.2 between the cylinder and the incline. When the cylinder reaches the bottom of the incline, its total kinetic energy is (g=10m/s2)
View SolutionA solid cylinder is rolling down a rough inclined plane of inclination θ. Then
View SolutionA solid cylinder of mass m is kept in balance on a fixed incline of angle α=37∘ with the help of a thread fastened to its jacket. The cylinder does not slip.

The values of minimum coefficient of static friction between cylinder and incline in the case when F is minimum.
View Solution
