A cylinder is released from the top of an incline making angle θ=45∘ with the horizontal. The length of the incline is 2.82m and mass of cylinder is 1kg. The coefficient of friciton is 0.2 between the cylinder and the incline. When the cylinder reaches the bottom of the incline, its total kinetic energy is (g=10m/s2)
Equal to 20 joule
Greater than 20 joule
Less than 20 joule
28.2 joule
To solve the problem step by step, we will calculate the total kinetic energy of the cylinder when it reaches the bottom of the incline.
Step 1: Identify the parameters
- Mass of the cylinder (m) = 1 kg
- Length of the incline (L) = 2.82 m
- Angle of incline (θ) = 45°
- Gravitational acceleration (g) = 10 m/s²
- Coefficient of friction (μ) = 0.2
Step 2: Calculate the vertical height (h) of the incline
The vertical height can be calculated using the sine function:
h=L⋅sin(θ)
Substituting the known values:
h=2.82⋅sin(45°)
Since sin(45°)=1√2≈0.707:
h=2.82⋅0.707≈2.0 m
Step 3: Calculate the gravitational potential energy (PE) at the top
The gravitational potential energy at the top of the incline is given by:
PE=m⋅g⋅h
Substituting the values:
PE=1⋅10⋅2.0=20 J
Step 4: Determine the work done by friction
In this case, the cylinder rolls down the incline without slipping, which means it undergoes pure rolling motion. Therefore, the work done by friction is zero.
Step 5: Apply conservation of mechanical energy
Since the work done by friction is zero, the total mechanical energy is conserved. Thus, the total kinetic energy (KE) at the bottom of the incline is equal to the potential energy at the top:
KE=PE
From our previous calculation:
KE=20 J
Step 6: Conclusion
The total kinetic energy of the cylinder when it reaches the bottom of the incline is 20 J.
Final Answer
The total kinetic energy at the bottom of the incline is 20 J.
---
- Mass of the cylinder (m) = 1 kg
- Length of the incline (L) = 2.82 m
- Angle of incline (θ) = 45°
- Gravitational acceleration (g) = 10 m/s²
- Coefficient of friction (μ) = 0.2
The vertical height can be calculated using the sine function:
h=L⋅sin(θ)
Substituting the known values:
h=2.82⋅sin(45°)
Since sin(45°)=1√2≈0.707:
h=2.82⋅0.707≈2.0 m
The gravitational potential energy at the top of the incline is given by:
PE=m⋅g⋅h
Substituting the values:
PE=1⋅10⋅2.0=20 J
In this case, the cylinder rolls down the incline without slipping, which means it undergoes pure rolling motion. Therefore, the work done by friction is zero.
Since the work done by friction is zero, the total mechanical energy is conserved. Thus, the total kinetic energy (KE) at the bottom of the incline is equal to the potential energy at the top:
KE=PE
From our previous calculation:
KE=20 J
The total kinetic energy of the cylinder when it reaches the bottom of the incline is 20 J.
The total kinetic energy at the bottom of the incline is 20 J.
Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Assignment (Section - C) Objective Type Questions (More than one option are correct)
29 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Assignment (Section - D) Linked Comprehension Type Questions
20 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Assignment (Section - A) Objective Type Questions (One option is correct)
62 Videos
- SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITSEXERCISE - Assignment (Section-D (Assertion and reason))
5 Videos
- TEST 1BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - TEST 1EXERCISE - EXERCISE
21 Videos
Similar Questions
A solid cylinder of mass M and radius R rolls from rest down a plane inclined at an angle θ to the horizontal. The velocity of the centre of mass of the cylinder after it has rolled down a distance d is :
View SolutionA uniform cylinder of mass m lies on a fixed plane inclined at a angle θ with the horizontal. A light string is tied to the cylinder at the rightmost point, and a mass m hangs from the string as shown. Assume that the coefficient of friction between the cylinder and the incline plane is sufficiently large to prevent slipping. for the cylinder to remain static the value of m is

View Solution
Knowledge Check
A solid cylinder of mass M and radius R rolls without slipping down an inclined plane making an angle 6 with the horizontal. Then its acceleration is.
A1/3 g sinθB2/3 g sinθC2/5 g sinθD2/7 g sinθ
A solid cylinder of mass m is kept in balance on a fixed incline of angle α=37∘ with the help of a thread fastened to its jacket. The cylinder does not slip.

The values of minimum coefficient of static friction between cylinder and incline in the case when F is minimum.
View SolutionA block of mass 8 kg is sliding on a surface inclined at an angle of 45∘ with the horizontal. Calculate the acceleration of the block. The coefficient of friction between the block and surface is 0.6. (Take g=10m/s2)
View SolutionA cylinder is released from rest from the top of an incline of inclination θ and length 'L'. If the cylinder rolls without slipping. What will be its speed when it reaches the bottom?
View SolutionA block of mass 8 kg is sliding on a surface inclined at an angle of 45∘ with the horizontal . Calculate the acceleration of the block . The coefficient of friction between the block and surface is 0⋅6 ( Take g = 10m/s2)
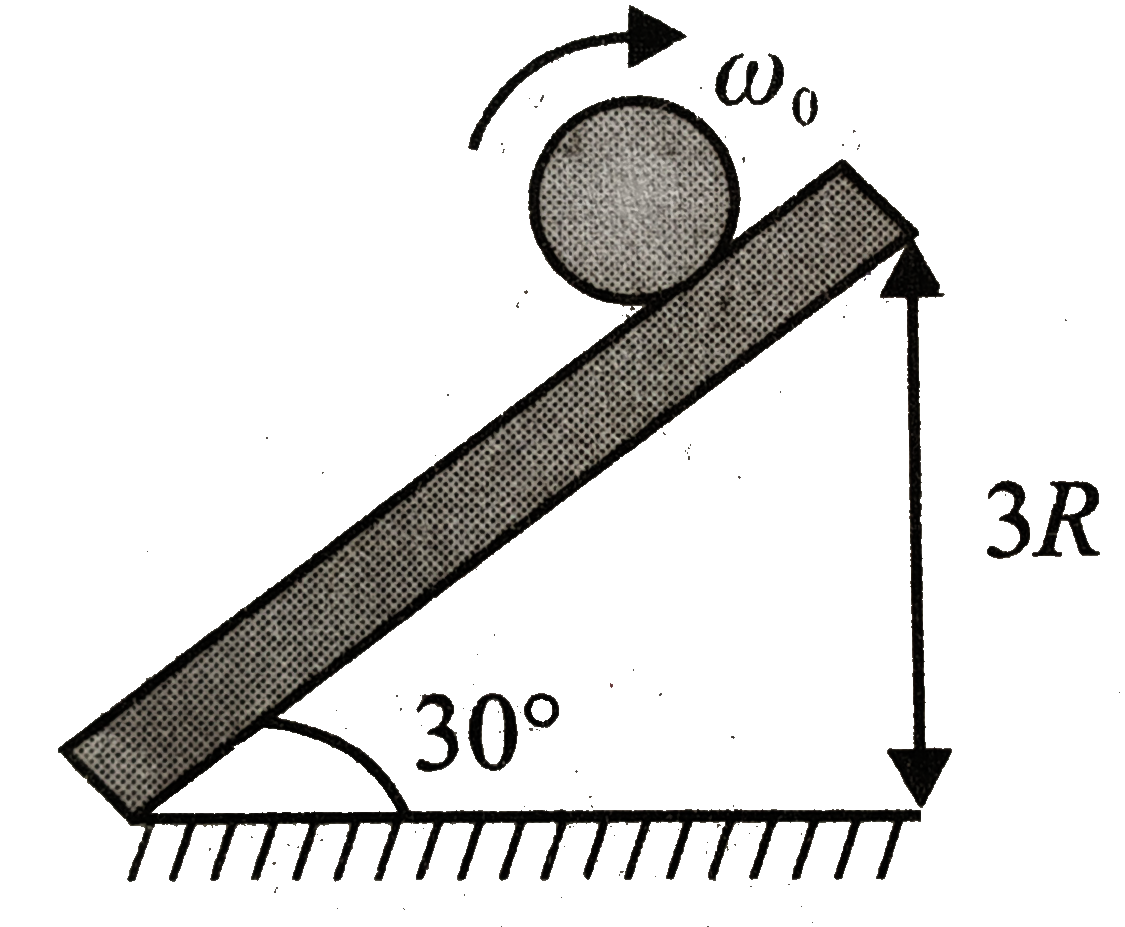
View SolutionA spinning cylinder with angular velocity ω0 of mass M and radius R is lowered on a rough inclined plane of angle 30∘ with the horizontal and μ=1/√3. The cylinder is released at a height of 3R from horizontal. Find the total time taken by the cylinder to reach the bottom of the incline.
View SolutionA cylinder rolls down on an inclined plane of inclination 37∘ from rest. Coefficient of friction between plane and cylinder is 0.5. Calculate the time ( in s) of travelling down the incline 8 m as shown in figure .(g=10m/s2)

View SolutionA solid cylinder of mass M and radius R rolls down an inclined plane of height h. The angular velocity of the cylinder when it reaches the bottom of the plane will be :
View Solution
