A uniform disc of mass $m$ is fitted (pivoted smoothly) with a rod of mass $m / 2$ . If the bottom of the rod os pulled with a velocity $v$ , it moves without changing its and of orientation and the disc rolls without sliding. Take kinetic energy of the system (rod + disc) is.
.

A

$\frac{m v^{2}}{4}$

B

$\frac{m v^{2}}{2}$

C

$\frac{5 m v^{2}}{16}$

D

$m v^{2}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

(d) Rolling can be considered as pure rotation about point of contact
$K_{rolling} = \frac{1}{2} I_{p} ω^{2} = \frac{1}{2} (\frac{m R^{2}}{2} + m R^{2}) ω^{2} = \frac{3}{4} m R^{2} ω^{2}$ …(i)
The rod translates with the velocity $v$ hence velocity of centre of disc will also be $v$
$v = ω R$ ...(ii)
From (i) and (ii) , $K_{rolling} = \frac{3}{4} m v^{2}$
Kinetic energy of the rod $K_{r o d} = \frac{1}{2} (\frac{m}{2}) v^{2} = \frac{m v^{2}}{4}$ ...(iii)
$K_{\to t a l} = k_{rolling} + k_{r o d} = m v^{2}$ .

|

Updated on:21/07/2023

Class 11 PHYSICS RIGID BODY DYNAMICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A circular disc of mass 2 kg and radius 10 cm rolls without slipping with a speed 2 m/s. The total kinetic energy of disc is
A10 J
B6 J
C2 J
D4 J
Question 2 - Select One
Four beads each of mass $m$ are glued at the top, bottom and the ends of the horizontal diameter of a ring of mass $m$ . If the ring rolls without sliding with the velocity $v$ of its, the kinetic energy of the system (beads+ring) is

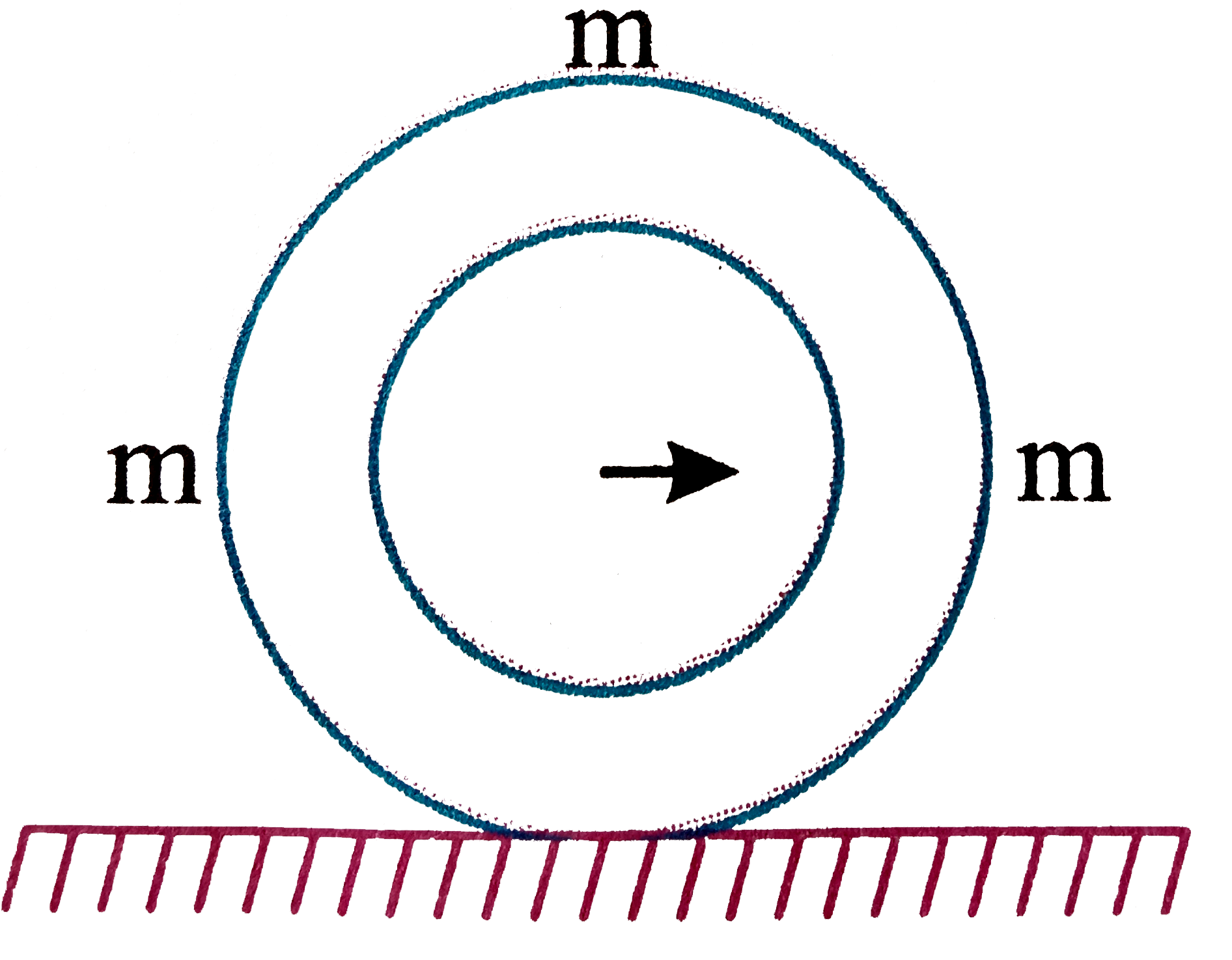A $5 m v^{2}$
B $4 m v^{2}$
C $2 m v^{2}$
D $m v^{2}$
Question 3 - Select One or More
A uniform rod of length $l$ and mass $2 m$ rests on a smooth horizontal table. A point of mass $m$ moving horizontally at right angle to the rod with velocity $v$ collides with one end of the rod and sticks to it, then:
Aangular velocity of the system after collision is $\frac{v}{l}$
Bangular velocity of the system after collision is $\frac{v}{2 l}$
Cthe loss in kinetic enerlgy of the system as a whole as a result of the collision is $\frac{m v^{2}}{6}$
Dthe loss in kinetic energy of the system as a whole as a result of the collision is $\frac{7 m v^{2}}{24}$

A2Z-ROTATIONAL DYNAMICS-Problems Based On Mixed Concepts

Home
Ask Doubt
Profile