A uniform disc of radius R is rolling (without slipping) on a horizontal surface with an angular speed ω as shown in the figure. O is the centre of the disc, points A and C are R. located on its rim and point B is at a distance R2 from O. During rolling, the points A, B and C come on the vertical diameter at a certain instant of time. If vAvBandvC are the linear speeds of points A, Band C respectively at that instant, then

vA0,vC=43vB
vA=0,vC=2vB
vA=vB=vC
VA>vB>vC
The correct Answer is:A
The axis of rotation passes through the point A and is perpendicular to the plane of the disc.
B is at a distance of R+R2=3R2 from A and C is at a distance of 2R from A.
∵v=rω ∴vA=0,vB=(3R2)ωandvC=(2R)ω
∴vCvB=2Rω×23Rω=43
Thus vA=0andvC=43vB
Topper's Solved these Questions
Similar Questions
A circular disc of radius r is rolling without slipping on a horizontal surface. What is the ratio of the translational KE and rotational KE of disc ?
View SolutionA disc of radius 0.2m is rolling with slipping on a flat horizontal surface, as shown in Fig. The instantaneous centre of rotation is (the lowest contact point is O and centre of disc is C)
View Solution
Knowledge Check
A disc of radius 0.2m is rolling with slipping on a flat horizontal surface, as shown in Fig. The instantaneous centre of rotation is (the lowest contact point is O and centre of disc is C)
 AzeroB0.1m above O on line OCC0.2m below O on line OCD0.2m above O on line OC
AzeroB0.1m above O on line OCC0.2m below O on line OCD0.2m above O on line OCA wheel of radius R rolls without slipping on a horizontal ground. The distance travelled by a point on the rim in one complete rotation is:
A2πRB8RC2RDπR
A uniform disc of radius R is in pure rolling on a fixed horizontal surface with constant speed v0 as shown in the figure. For what value of θ, speed of point P will be v02√(5+2√3) ? (OP= R/2 and O is the centre of disc)

View SolutionA circular disc of radius R rolls without slipping along the horizontal surface with constant velocity v0. We consider a point A on the surface of the disc. Then the acceleration of the point A is:
View SolutionA circular disc of radius R rolls without slipping along the horizontal surface with constant velocity v0. We consider a point A on the surface of the disc. Then the acceleration of the point A is:
View SolutionA uniform circular disc of radius R is rolling on a horizontal surface. Determine the tangential velocity : at the upper most point
View SolutionA disc rolls without slipping on a horizontal surface such that its velocity of center of the mass is v. Find the velocity of points A,B,C and D.

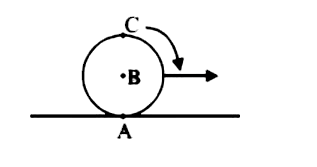
View SolutionA sphere is rolling without slipping on a fixed horizontal plane surface. In the figure, A is the point of contact, B is the centre of the sphere and C is its topmost point. Then :
View Solution
