A uniform disc of radius $R$ lies in the $x - y$ plane, with its centre at origin. Its moment of inertia about z-axis is equal to its moment of inertia about line $y = x + c$ . The value of $c$ will be.
.

A

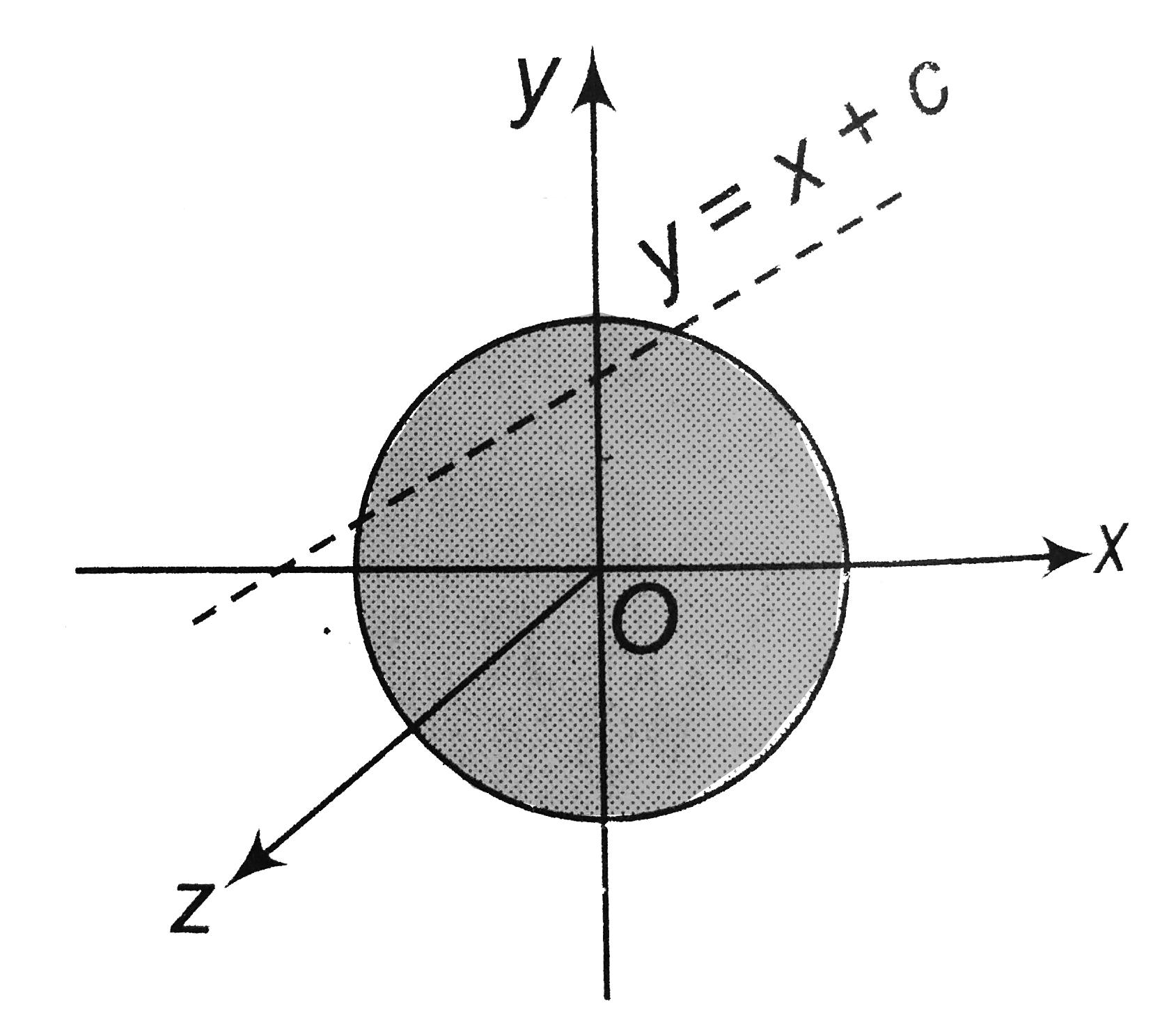$- \frac{R}{2}$

B

$\pm \frac{R}{\sqrt{2}}$

C

$\frac{+ R}{4}$

D

$- R$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

(b) $I_{P Q R} = I_{A O B} + M . {(O N)}^{2} I_{P Q R} = \frac{1}{4} M R^{2} + M . {(\frac{c}{\sqrt{2}})}^{2}$
But $I_{P Q R} = \frac{1}{2} M R^{2}$ :. $c = \pm \frac{R}{\sqrt{2}}$
Hence (b) is correct.
.

|

Updated on:21/07/2023

Class 11 PHYSICS RIGID BODY DYNAMICS

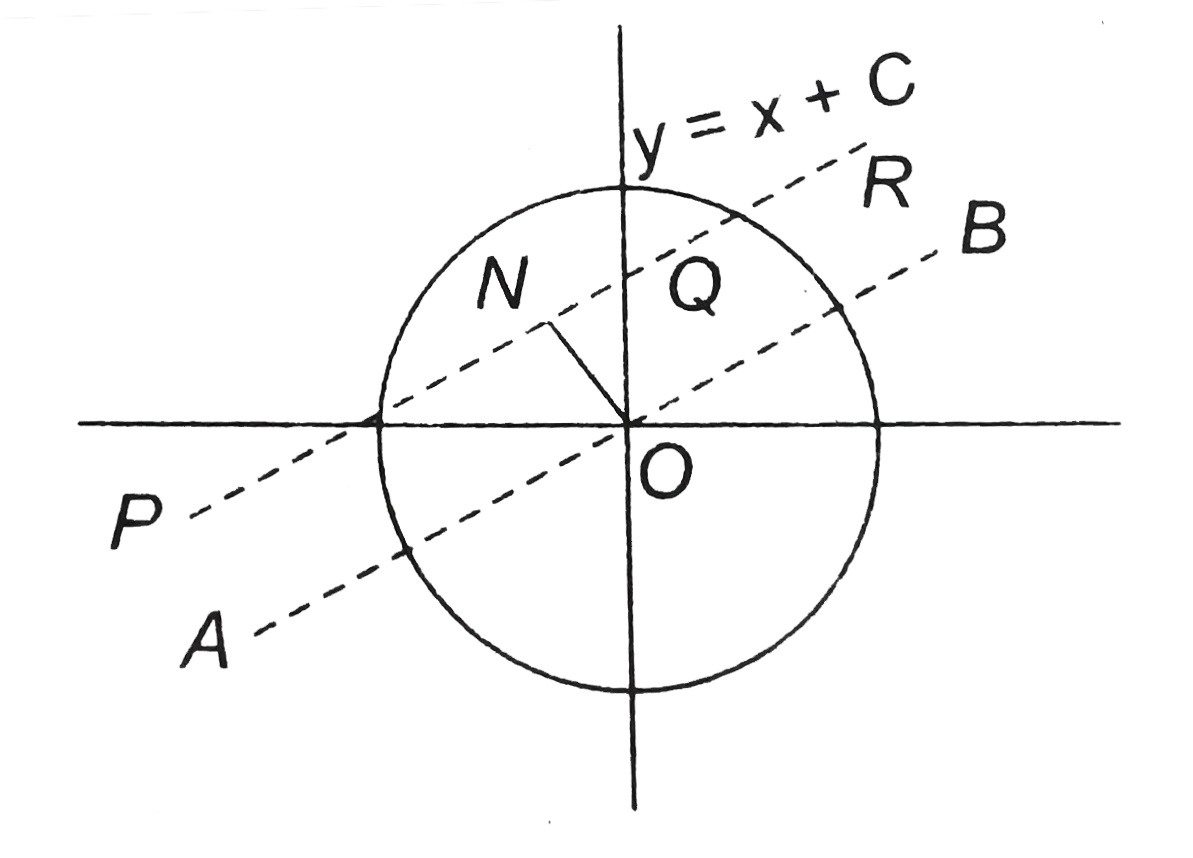Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A uniform disc of radius R lies in x-y plane with its centre at origin. Its moment of inertia about the axis x=2R and y=0 is equal to the moment of inertia about the axis y=d and z=0, where d is equal to
A $\frac{4}{3} R$
B $\frac{\sqrt{17}}{2} R$
C $\sqrt{13} R$
D $\frac{\sqrt{15}}{2} R$
Question 2 - Select One
A uniform disc of radius $R$ lies in xy-plane with its centre at origin. Its moments of inertia about the axis $X = 2 R$ and $Y = 0$ is equal to the moment of inertia about the axis $Y = d$ and $Z = 0$ . What is the value of $d$ ?
A $\frac{\sqrt{17}}{2} R$
B $\sqrt{13} R$
C $\sqrt{\frac{15}{2}} R$
D $\frac{4}{3} R$
Question 3 - Select One
A uniform disc of radius R lies in xy plane with its centre at origin. Its moment of inertia about the axis x = 2 R and y =0 is equal to the moment of inertia about the axis y =d and z = 0. What is d equal to ?
A $\frac{\sqrt{17}}{2} R$
B $\sqrt{13} R$
C $\frac{\sqrt{15}}{2} R$
D $\frac{4}{3} R$

A2Z-ROTATIONAL DYNAMICS-Moment Of Inertia

Home
Ask Doubt
Profile