A uniform iron rod of length 50 cm is bent, at right angles at 30 cm from one end, giving it an L-shape. The L-shaped rod is suspended freely from its point of bending. Find the angle that the 30 cm arm makes with the vertical at equilibrium.
Suppose the rod is bent at the point B Fig. AB=20 cm , BC=30 cm , and B is the point of suspension. Suppose BC in equilibrium, makes an angle θ with the vertical.
Let the mass per unit length of the rod be w. So mass of AB is 20 w and mass of BC is 30 w. At equilibrium, the moments about the point B due to the two masses, shoud be equal. Let x and y be the perpendicular distances of the centres of mass of the arms AB and BC respectively, from the vertical line through B. The centre of mass is at the midpoint of each arm.
∴20wx=30wy
or, 20×10cosθ=30×15sinθor,tanθ=49
or, θ=24∘.

Topper's Solved these Questions
- STATICSBOOK - CHHAYA PUBLICATIONCHAPTER - STATICSEXERCISE - HIGHER ORDER THINKING SKILL (HOTS) QUESTIONS
18 Videos
- STATICSBOOK - CHHAYA PUBLICATIONCHAPTER - STATICSEXERCISE - EXERCISE (Multiple Choice Questions )
14 Videos
- SIMPLE HARMONIC MOTIONBOOK - CHHAYA PUBLICATIONCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - CBSE SCANNER
16 Videos
- SUPERPOSITION OF WAVESBOOK - CHHAYA PUBLICATIONCHAPTER - SUPERPOSITION OF WAVESEXERCISE - CBSE Scanner
14 Videos
Similar Questions
A uniform thin rod of length 3L is bent at right angles at a distance L from one end as shown in Fig. If length of rod is 1.8m, find the co-ordinates and position vector of the mass of the system.

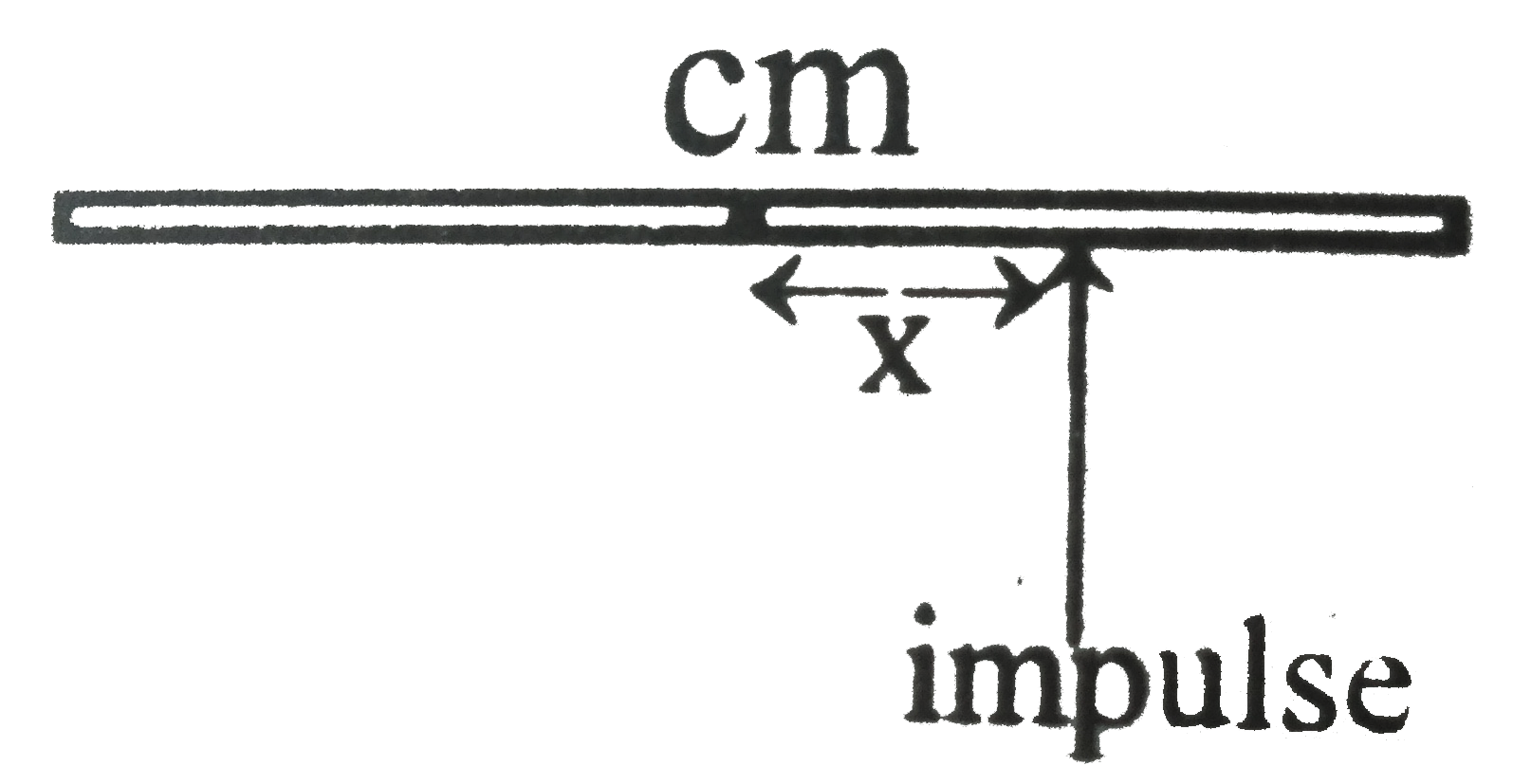
View SolutionA uniform rod of length l is given an impulse at right angles to its length as shown. Find the distance of instantaneous centre of rotation from the centre of the rod.
 .
.
View Solution
Knowledge Check
A rod of length l=100cm is fixed at 30cm from both end. If velocity of transverse wave in rod is v(cms−1), then chose the correct option(s)
AFundamental frequencey (in Hz) of transverse wave in rod is v40BSecond overtone in rod will 5th harmonicCFrequency of third overtone (in Hz) is 7v/40DThird overtone is5th harmonicA uniform rod o length one meter is bent at its midpoint to make 90∘. The distance of centre of mass from the centre of rod is (in cm)
A20.2B13.4C15D17.6A uniform thin rod of length l is suspended from one of its ends and is rotated at f rotations per second. The rotational kinetic energy of the rod will be
A23π2f2ml2B43f2ml2C4π2f2ml2Dzero
A rod of length l=100cm is fixed at 30cm from both end. If velocity of transverse wave in rod is v(cms−1), then chose the correct option(s)
View SolutionA L shaped, uniform rod has its two arms of length l and 2l. It is placed on a horizontal table and a string is tied at the bend. The string is pulled horizontally so that the rod slides with constant speed. Find the angle θ that the longer side makes with the string. Assume that the rod exerts uniform pressure at all points on the table.

View SolutionA rod of length l is pivoted about a horizontal , frictionless pin through one end. The rod is released from ret in a vertical position. Find the velocity of the CM of the rod when the rod is inclined at an angle θ from the vertical.

View SolutionA rod of length l is pivoted about a horizontal , frictionless pin through one end. The rod is released from ret in a vertical position. Find the velocity of the CM of the rod when the rod is inclined at an angle θ from the vertical.

View SolutionA uniform thin rod of length l is suspended from one of its ends and is rotated at f rotations per second. The rotational kinetic energy of the rod will be
View Solution
