A uniform thin rod of length l is suspended from one of its ends and is rotated at f rotations per second. The rotational kinetic energy of the rod will be
2mL2π2n2
12mL2π2n2
23mL2π2n2
16mL2π2n2
The correct Answer is:C
To find the rotational kinetic energy of a uniform thin rod of length l suspended from one of its ends and rotated at f rotations per second, we can follow these steps:
Step 1: Understand the given parameters
- Length of the rod = l
- Frequency of rotation = f rotations per second
Step 2: Identify the formula for rotational kinetic energy
The formula for rotational kinetic energy K is given by:
K=12Iω2
where I is the moment of inertia and ω is the angular velocity.
Step 3: Calculate the moment of inertia of the rod
For a uniform thin rod of length l suspended from one end, the moment of inertia I is given by:
I=13ml2
where m is the mass of the rod.
Step 4: Convert frequency to angular velocity
The angular velocity ω can be calculated from the frequency f using the relation:
ω=2πf
Step 5: Substitute I and ω into the kinetic energy formula
Substituting the values of I and ω into the kinetic energy formula:
K=12(13ml2)(2πf)2
Step 6: Simplify the expression
Now, simplify the expression:
K=12⋅13ml2⋅4π2f2
K=23ml2π2f2
Final Result
Thus, the rotational kinetic energy of the rod is:
K=23ml2π2f2
- Length of the rod = l
- Frequency of rotation = f rotations per second
The formula for rotational kinetic energy K is given by:
K=12Iω2
where I is the moment of inertia and ω is the angular velocity.
For a uniform thin rod of length l suspended from one end, the moment of inertia I is given by:
I=13ml2
where m is the mass of the rod.
The angular velocity ω can be calculated from the frequency f using the relation:
ω=2πf
Substituting the values of I and ω into the kinetic energy formula:
K=12(13ml2)(2πf)2
Now, simplify the expression:
K=12⋅13ml2⋅4π2f2
K=23ml2π2f2
Thus, the rotational kinetic energy of the rod is:
K=23ml2π2f2
Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - VMC MODULES ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - IMPECCABLE
56 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - VMC MODULES ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - ENABLE
50 Videos
- SYSTEM OF A PARTICLES & ROTATIONAL MOTIONBOOK - VMC MODULES ENGLISHCHAPTER - SYSTEM OF A PARTICLES & ROTATIONAL MOTIONEXERCISE - IN-CHAPTER EXERCISE F
10 Videos
- UNITS, MEASUREMENTS & ERRORSBOOK - VMC MODULES ENGLISHCHAPTER - UNITS, MEASUREMENTS & ERRORSEXERCISE - IN - CHAPTER EXERCISE - B
10 Videos
Similar Questions
A uniform rod of mass m and length l is suspended about its end. Time period of small angular oscillations is

View SolutionA uniform rod mass m and length l is provided at one end and is rotated with constant angular velocity ω in a horizontal plane. Tension in the rod at a distance (√3l/2) from pivoted end is (Assume gravity free space)
View SolutionA uniform thin rod of length l and mass m is hinged at a distance l/4 from one of the end and released from horizontal position as shown in Fig. The angular velocity of the rod as it passes the vertical position is

View SolutionTwo beads each of mass m are welded at the ends of two light rigid rods each of length l. if the pivots are smooth, find the ratio of translational and rotational kinetic energy of system.
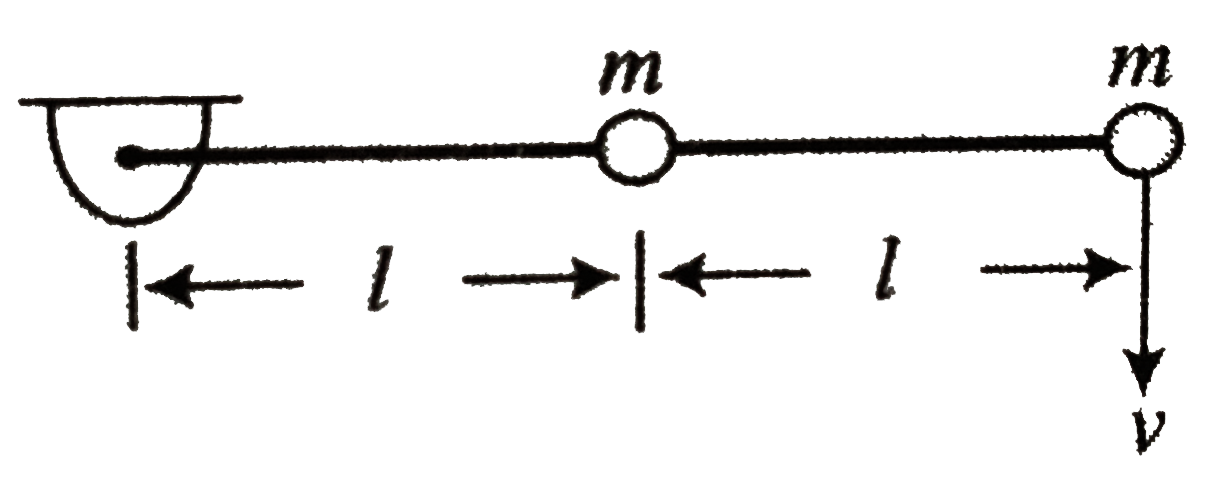
View SolutionA uniform rod of length l is from rest such that it rotates about a smooth pivot. The angular speed of the rod when it becomes vertical is.
 .
.
View SolutionA uniform rod of mass m and length L lies radialy on a disc rotating with angular speed ω in a horizontal plane about vertical axis passing thorugh centre of disc. The rod does not slip on the disc and the centre of the rod is at a distance 2L from the centre of the disc. them the kinetic energy of the rod is

View SolutionA non–uniform thin rod of length L is placed along x-axis as such its one of ends at the origin. The linear mass density of rod is λ=λ0x. The distance of centre of mass of rod from the origin is :
View SolutionA uniform rod of length L, has a mass per unit length λ and area of cross section A. The elongation in the rod is l due to its own weight, if it suspended form the celing of a room. The Young's modulus of the rod is
View SolutionA rod of mass m and length l is connected with a light rod of length l. The composite rod is made to rotate with angular velocity ω as shown in the figure. Find the
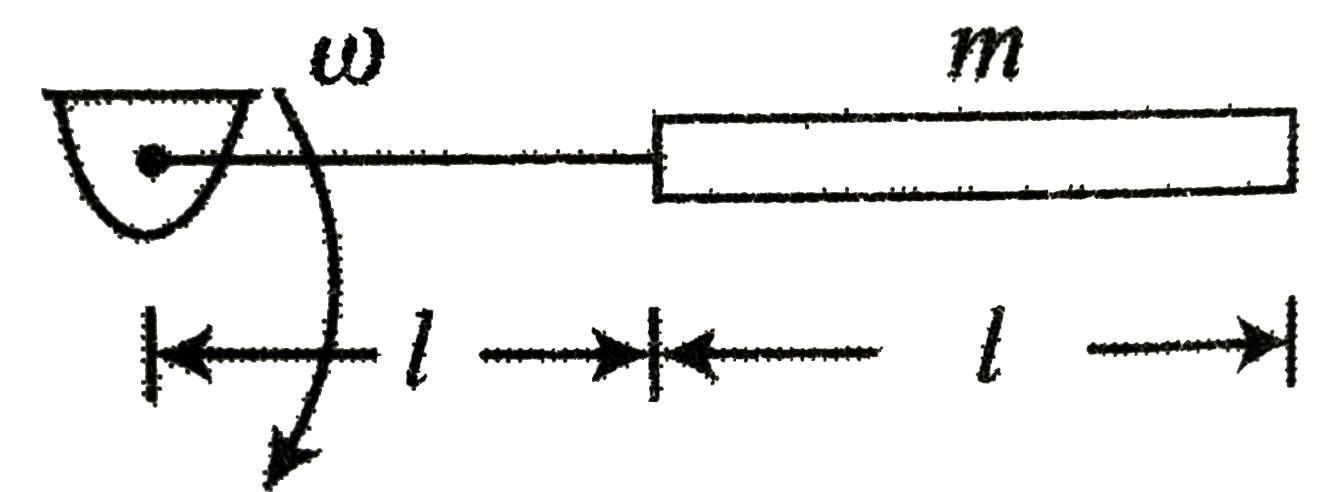
a. translational kinetic energy.
b. rotational kinetic energy.
c. total kinetic energy of rod.
View SolutionA uniform rod of mass m and length l is fixed from Point A, which is at a distance l/4 from one end as shown in the figure. The rod is free to rotate in a vertical plane. The rod is released from the horizontal position.

What is the reaction at the hinge, when kinetic energy of the rod is maximum?
View Solution
