A uniform magnetic field B exist in a direction perpedicuar to the plane of a square loop made of a metal wire. The wire has diameter of 4 mm and a total length of 30 cm . The magnetic field changes with time at a steady rate dB/dt = 0.032 Ts−1 . The induced current in the loop is close to (Resistivity of the metal wire is 1.23×10−8Ωm)
0.53 A
0.34 A
0.61 A
0.43 A
To solve the problem of finding the induced current in a square loop of wire placed in a changing magnetic field, we can follow these steps:
Step 1: Calculate the Area of the Square Loop
Given that the total length of the wire is 30 cm, we can find the side length of the square loop.
- The perimeter of the square loop is equal to the total length of the wire:
P=4a=30 cm=0.30 m
where a is the side length of the square.
- Solving for a:
a=30 cm4=7.5 cm=0.075 m
- The area A of the square loop is:
A=a2=(0.075 m)2=0.005625 m2
Step 2: Calculate the Resistance of the Wire
The resistance R of the wire can be calculated using the formula:
R=ρLA
where:
- ρ=1.23×10−8Ω⋅m (resistivity of the metal),
- L=0.30m (length of the wire),
- A is the cross-sectional area of the wire.
First, we need to find the cross-sectional area A of the wire:
- The diameter of the wire is 4 mm, hence the radius r is:
r=4 mm2=2 mm=2×10−3 m
- The cross-sectional area A of the wire is:
A=πr2=π(2×10−3)2=π×4×10−6≈1.25664×10−5 m2
Now substituting into the resistance formula:
R=(1.23×10−8)×0.301.25664×10−5≈2.94×10−4Ω
Step 3: Calculate the Induced EMF
According to Faraday's law of electromagnetic induction, the induced EMF E is given by:
E=−dΦdt
where Φ=B⋅A is the magnetic flux.
Since the area is constant and the magnetic field B is changing, we can express the change in flux as:
E=AdBdt
Substituting the values:
E=(0.005625m2)×(0.032T/s)=0.000180V=0.180mV
Step 4: Calculate the Induced Current
Using Ohm's law, the induced current I can be calculated as:
I=ER
Substituting the values:
I=0.0001802.94×10−4≈0.612A
Final Answer
The induced current in the loop is approximately 0.612A.
---
Given that the total length of the wire is 30 cm, we can find the side length of the square loop.
P=4a=30 cm=0.30 m
where a is the side length of the square.
a=30 cm4=7.5 cm=0.075 m
A=a2=(0.075 m)2=0.005625 m2
The resistance R of the wire can be calculated using the formula:
R=ρLA
where:
- ρ=1.23×10−8Ω⋅m (resistivity of the metal),
- L=0.30m (length of the wire),
- A is the cross-sectional area of the wire.
- The diameter of the wire is 4 mm, hence the radius r is:
r=4 mm2=2 mm=2×10−3 m
A=πr2=π(2×10−3)2=π×4×10−6≈1.25664×10−5 m2
R=(1.23×10−8)×0.301.25664×10−5≈2.94×10−4Ω
According to Faraday's law of electromagnetic induction, the induced EMF E is given by:
E=−dΦdt
where Φ=B⋅A is the magnetic flux.
E=AdBdt
Substituting the values:
E=(0.005625m2)×(0.032T/s)=0.000180V=0.180mV
Using Ohm's law, the induced current I can be calculated as:
I=ER
Substituting the values:
I=0.0001802.94×10−4≈0.612A
The induced current in the loop is approximately 0.612A.
Topper's Solved these Questions
Similar Questions
A uniform magnetic field B exists in a direction perpendicular to the plane of a square frame made of copper wire. The wire has a diameter of 2 mm and a total length of 40cm. The magntic field changes with time at a steady rate dBdt=0.02Ts−1.F∈dthecurrent∈duced∈theame.Resistivityofcopper=1.7 X 10 ^(-8) Wm.
View SolutionA uniform magnetic field B exists in a direction perpendicular to the palne of a square frame made of copper wire. The wire has a total length of 40cm . The magnetic field changes with time at a steady rate (dB/dt)=0.02T/sec . Find the current induced in the frame. Resistance of wire =I0Ω
View Solution
Knowledge Check
ABCD is a square loop made of a uniform conducting wire. A current enters the loop at A and leaves at D. The magnetic field is
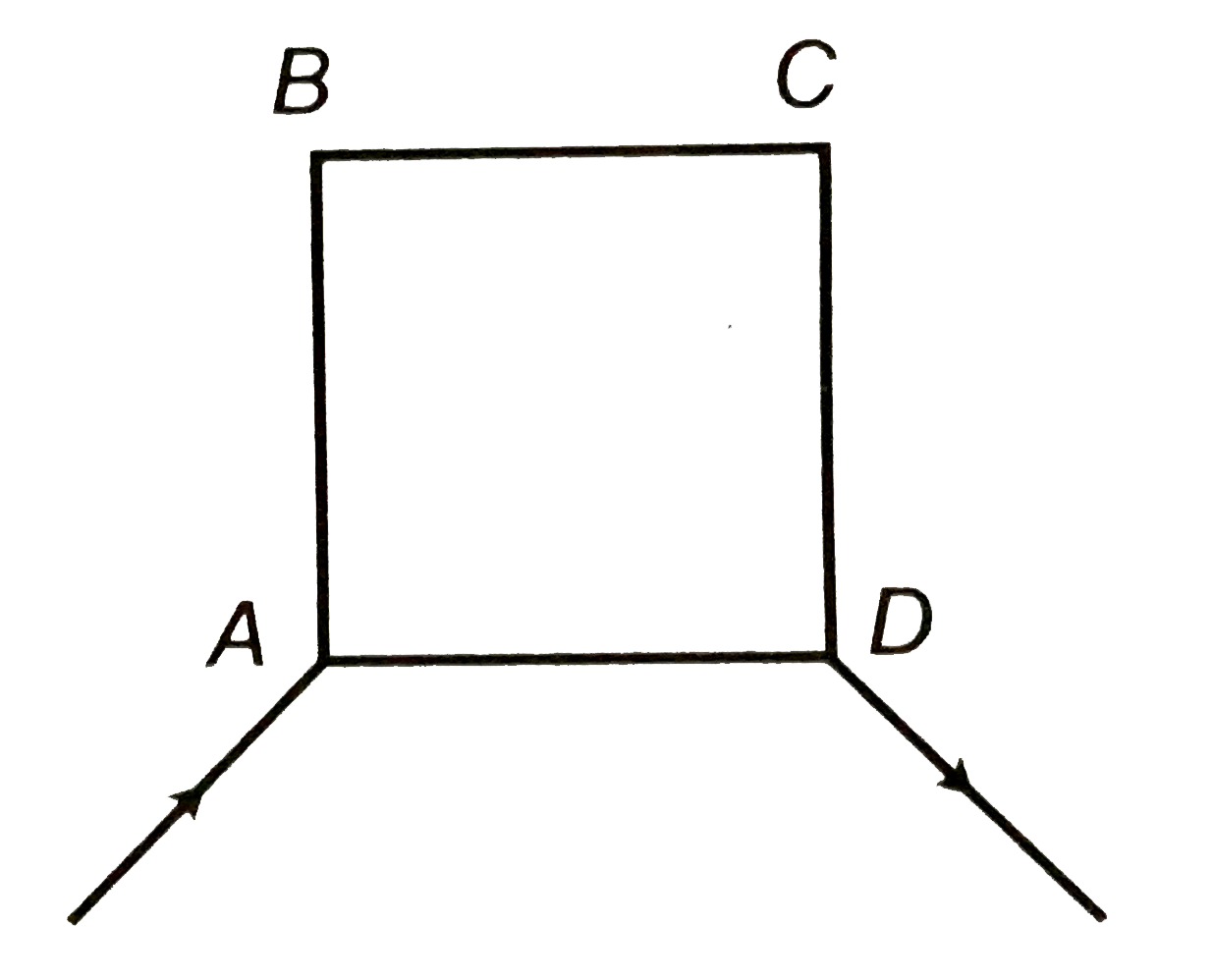 Azero only at the centre of the loopBmaximum at the centre of the loopCzero at all point outside the centre loopDzero at all points inside the loop
Azero only at the centre of the loopBmaximum at the centre of the loopCzero at all point outside the centre loopDzero at all points inside the loopA square wire loop of side 30cm & wire cross section having diameter 4mm is placed perpendicular to a magnetic field changing at the rate 0.2 T/s. Final induced current in the wire loop.
(Given: Resistivity of wire material is (1.23×10−8ohmm)A5.34×102 AB3.34×102 AC7.34×102 AD1.34×102 AThe magnetic field perpendicular to the plane of a conducting ring of radius r changes at the rate.dBdt . Then
Athe emf induced in the ring is πr2dBdtBthe emf induced in the ring is 2πrdBdtCdiametrically opposite points on the ring are at the same potentialDall points on the ring are at the same potential
Magnetic Field || Wire || Loop
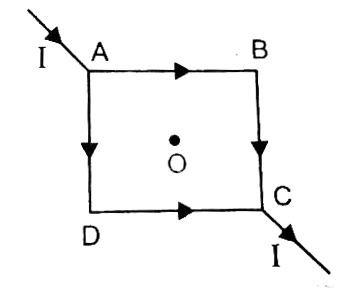
View SolutionFigure shows a square loop made from a uniform wire. If a battery is connected between the pionts A and C. What will be the magnetic field at the centre O of the square?
View SolutionThe magnetic field perpendicular to the plane of a conducting ring of radius r change ate the rate dBdt
View SolutionA rectangular loop of metallic wire is of length a and breadth b and carries a current i. The magnetic field at the centre of the loop is
View SolutionA square conductind loop, 20.0cm on a side placed in the same magnetic field as shown in Fig. 3.195, center of the magnetic field region, where dB/dt=0.035Ts−1.

he direction of induced electric field at points a, b and c:
View Solution
