A uniform magnetic field of 1 Tesla in space. The velocity of particle is V perpendicular to the magnetic field intensity. Find the radius of circular path followed by the particle. How much time will the particle take to complete one revolution? mass of particle is m and charge on particle is q
To solve the problem step by step, we will derive the radius of the circular path followed by a charged particle in a magnetic field and the time taken to complete one revolution.
Step 1: Understand the Forces Acting on the Particle
When a charged particle with charge q moves with velocity v perpendicular to a magnetic field B, it experiences a magnetic force given by:
F=qvB
This force acts as the centripetal force that keeps the particle in circular motion.
Step 2: Set Up the Equation for Circular Motion
The centripetal force required to keep the particle moving in a circular path is given by:
Fc=mv2r
where m is the mass of the particle, v is its velocity, and r is the radius of the circular path.
Step 3: Equate the Magnetic Force and Centripetal Force
Since the magnetic force provides the necessary centripetal force, we can set the two forces equal to each other:
qvB=mv2r
Step 4: Solve for the Radius r
Rearranging the equation to solve for r:
r=mvqB
This gives us the radius of the circular path followed by the particle.
Step 5: Calculate the Time Taken for One Revolution
The distance traveled in one complete revolution (circumference of the circle) is:
s=2πr
The time T taken to complete one revolution is given by:
T=sv=2πrv
Substituting r from Step 4:
T=2π(mvqB)v
This simplifies to:
T=2πmqB
Final Answers
1. The radius of the circular path is:
r=mvqB
2. The time taken to complete one revolution is:
T=2πmqB
When a charged particle with charge q moves with velocity v perpendicular to a magnetic field B, it experiences a magnetic force given by:
F=qvB
This force acts as the centripetal force that keeps the particle in circular motion.
The centripetal force required to keep the particle moving in a circular path is given by:
Fc=mv2r
where m is the mass of the particle, v is its velocity, and r is the radius of the circular path.
Since the magnetic force provides the necessary centripetal force, we can set the two forces equal to each other:
qvB=mv2r
Rearranging the equation to solve for r:
r=mvqB
This gives us the radius of the circular path followed by the particle.
The distance traveled in one complete revolution (circumference of the circle) is:
s=2πr
The time T taken to complete one revolution is given by:
T=sv=2πrv
Substituting r from Step 4:
T=2π(mvqB)v
This simplifies to:
T=2πmqB
1. The radius of the circular path is:
r=mvqB
2. The time taken to complete one revolution is:
T=2πmqB
Topper's Solved these Questions
- BOOK - MODERN PUBLICATIONCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - PRACTICE PROBLEMS59videos
MOVING CHARGES AND MAGNETISM
- BOOK - MODERN PUBLICATIONCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - Conceptual Questions29videos
MOVING CHARGES AND MAGNETISM
- BOOK - MODERN PUBLICATIONCHAPTER - MAGNETISM AND MATTEREXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION16videos
MAGNETISM AND MATTER
- BOOK - MODERN PUBLICATIONCHAPTER - NUCLEIEXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION15videos
NUCLEI
Similar Questions
Magnetic force acting on the charged particle projected perpendicular to magnetic field is proportional to rn, where r is radius of circular path. Find n
View SolutionA charged particle enters a uniform magnetic field with velocity v0=4m/s perpendicular to it, the length of magnetic field is x=(√32)R, where R is the radius of the circular path of the particle in the field. Find the magnitude of charge in velocity (in m/s) of the particle when it comes out of the field.
View Solution
Knowledge Check
- Question 1 - Select One
If a charged particle enters perpendicular in the uniform magnetic field then
AEnergy remains constant but moment changesBEnergy and momentum both remains constantCMomentum remains constant but energy changesDNeither energy nor momentum remains constant - Question 2 - Select One
A charged particle enters into a uniform magnetic field with velocity v0 perpendicular to it , the length of magnetic field is x=√32R, where R is the radius of the circular path of the particle in the field .The magnitude of change in velocity of the particle when it comes out of the field is
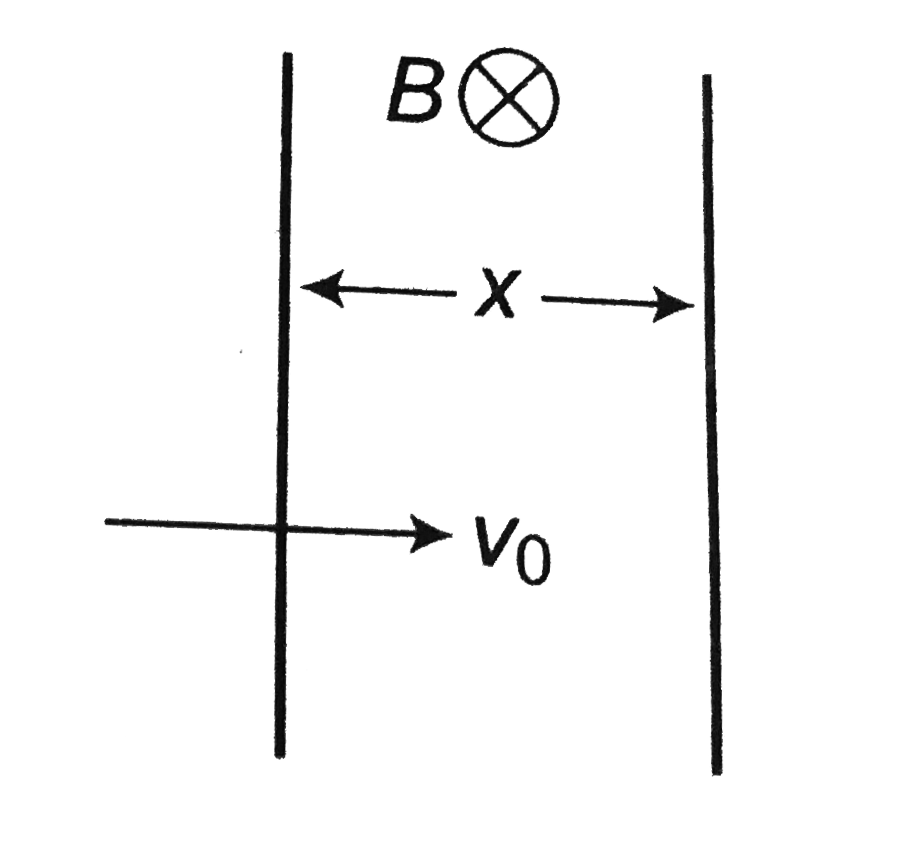 A2v0Bv0/(2)C√3v02Dv0
A2v0Bv0/(2)C√3v02Dv0 - Question 3 - Select One
If a charged particle is a plane perpendicular to a uniform magnetic field with a time period T Then
AT2∝r3BT2∝rCT∝r2DT∝r0
What will be the path of a charged particle moving perpendicular to a uniform magnetic field?
View SolutionWhen a charged particle is projected perpendicular to the magnetic field, the force acting on the charged particle is……………of the radius of circular path but…………….the speed of the charged particle.
View SolutionA particle of mass m, charge e and velocity v moving in a magnetic field B perpendicular to the motion of particle. The radius of its path is:
View SolutionA charged particle enters a uniform magnetic field with velocity vector at angle of 45∘ with the magnetic field. The pitch of the helical path followed by the particle is p. the radius of the helix will be
View SolutionA particle carrying a charge moves perpendicular to a uniform magnetic field of induction B with a momentum p then the radius of the circular path is
View Solution

