A uniform magnetic field of 3000G is established along the positive z-direction. A rectangular loop of sides 10cm and 5cm carries a current 12A. What is the torque on the loop in the different cases shown in the figure. What is the force on each case? Which case corresponds to stable equilibrium?

(a) Torque on a loop of area →A, carrying a current I placed in an external magnetic field →B is given by:
→τ=I(→A×→B)
Here, B=3,000G=3,000×10−4T=0.3T
Since B is along the positive Z-axis,
→B=0.3ˆkT
A=10×5=50cm2=50100×100m2=5×10−3m2
Since current flowing in the loop is in the anticlockwise direction and the loop is lying in the Z-Y plane, the area veclor of the loup will be along positive X-axis.
→A=5×10−3ˆi
I=12A
⇒→τ=I(→A×→B)=12[(5×10−3ˆi)×(0.3ˆk)]
=−1.8×10−2ˆjNm
Torque acting on the rod will be along negative Y-axis.
(b) Since →B is along positive Z-axis,
→B=0.3ˆkT
Since current flowing in the loop is in the anticlockwise direction and the loop is lying in the Z-Y plane, the area vector of the loop will be along positive X-axis.
→A=5×10−3ˆim2
⇒ →τ=I(→A×→B)=12[(5×10−3ˆi)×(0.3ˆk)]
=−1.8×10−2ˆj N m
Torque acting on the rod will be along negative Y-axis.
(c) Since →B is along positive Z - axis ,
→B=0.3ˆk
Since current flowing in the loop is in the clockwise direction and the loop is lying in the X-Z plane, the area vector of the loop will be along negative Y axis
→A=5×10−3(−ˆj)m3
⇒ ˆτ=I(→A×→B)=12[(−5×10−3ˆj)×(0.3ˆk)]
=−1.8×10−2ˆi N m
Torque acting on the rod will be along negative X - axis.
(d) The current is flowing in the anticlockwise direction and the loop is oriented at an angle of 30∘ from the Z-Y plane. Thus, area vectors is given by:
→A=Asin30∘(−ˆj)+Acos30∘(ˆi)
=5×10−3[√32ˆi−12ˆj]m2
→B=0.3ˆkT
⇒ˆτ=I(→A×→B)=12[5×10−3(√32ˆi−12ˆj)×(0.3ˆk)]
=−0.9×10−2(ˆi+√3ˆj)Nm
|→τ|=1.8×10−2Nm
Torque acting on the rod is at an angle of 240∘ with the positive X direction.
(e) →B=0.3ˆkT
Since current flowing in the loop is in the anticlockwise direction and the loop is lying in the X-Y plane, the area vector of the loop will be along positive Z - axis
→A=5×10−3ˆk
⇒ →τ=I(→A×→B)=12[(5×10−3ˆk)×(0.3ˆk)]=0
(f) →B=0.3ˆk
Since current flowing in the loop is in the clockwise direction and the loop is lying in the X-Y plane, the area vector of the loop will be along negative Z-axis.
→A=−5×10−3ˆk
⇒→τ=I(→A×→B)=12[(−5×10−3ˆk)×(0.3ˆk)]=0
As the loop is closed and placed in a uniform magnetic field, force is zero in each case. Case (e) corresponds to a stable equilibrium because in this case, force and torque acting on the loop are both zero. Also, the magnetic moment of the loop given by M=I→A is along the direction of →B. Case (f) corresponds to unstable equilibrium because the magnetic moment in this case is opposite to the direction of B.
Topper's Solved these Questions
- BOOK - MODERN PUBLICATIONCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - NCERT (Exemplar Problems ) Objective Questions (MCQ Type - I)6videos
MOVING CHARGES AND MAGNETISM
- BOOK - MODERN PUBLICATIONCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - NCERT (Exemplar Problems ) Objective Questions (MCQ Type - II)5videos
MOVING CHARGES AND MAGNETISM
- BOOK - MODERN PUBLICATIONCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - NCERT FILE (NCERT Textbook Exercises)13videos
MOVING CHARGES AND MAGNETISM
- BOOK - MODERN PUBLICATIONCHAPTER - MAGNETISM AND MATTEREXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION16videos
MAGNETISM AND MATTER
- BOOK - MODERN PUBLICATIONCHAPTER - NUCLEIEXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION15videos
NUCLEI
Similar Questions
A unform magnetic field of 3000 G is established along the positive z-direction. A rectangular loop of sides 10 cm and 5 cm carries a current of 12 A . What is the torque on the loop in the different cases shown in the fig ? What is the force on each case? Which case corresponds to stable equilibrium ?
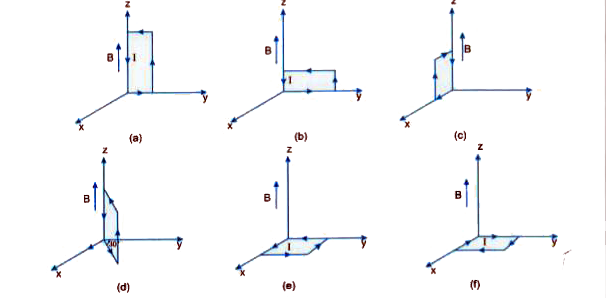 View Solution
View SolutionA square loop of side 15 cm carrying current of 10 A is kept at a distance of 5 cm from a long wire carrying 12 A current as shown in the adjoining figure. Calculate the net force acting on the loop.
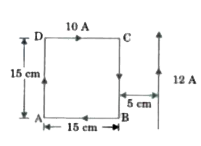 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A uniform magnetic field of 1000 G is established along the positive z-direction. A rectangular loop of sides 10 cm and 5 cm carries a current of 12 A. What is the torque on the loop as shown in the figure?
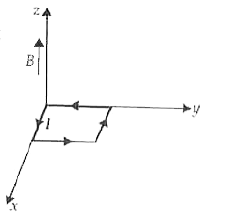 AzeroB1.8×10−2NmC1.8×10−3NmD1.8×10−4Nm
AzeroB1.8×10−2NmC1.8×10−3NmD1.8×10−4Nm - Question 2 - Select One
A uniform magnetic field of 1000 G is established along the positive z-direction. A rectangular loop of sides 10 cm and 5 cm carries a current of 12 A. What is the torque on the loop as shown in the figure?
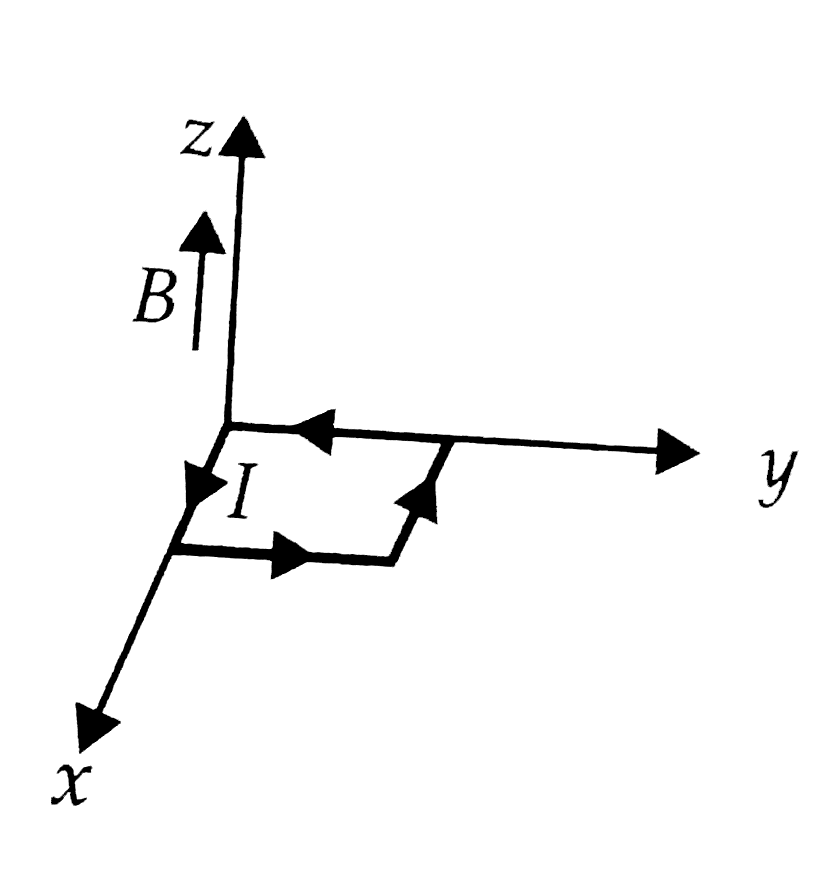 AZeroB1.8×10−2NmC1.8×10−3NmD1.8×10−4Nm
AZeroB1.8×10−2NmC1.8×10−3NmD1.8×10−4Nm - Question 3 - Select One
A uniformi magnetic field of 3 T is established along the positive Z-direction. A rectangular loop in XY plane of sides 10 cm and 5 cm carries a current of 11 A as shown The torque on the loop is:
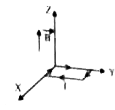 A+1.8×10−2ˆjNmB−1.8×10−2ˆjNmCZeroD−1.8×10−2ˆjNm
A+1.8×10−2ˆjNmB−1.8×10−2ˆjNmCZeroD−1.8×10−2ˆjNm
A rectangular loop of sides 25 cm and 10 cm carrying current of 15A is placed with its longer side parallel to a long straight conductor 2.0 cm apart carrying a current of 25A. What is the new force on the loop ?
View SolutionA uniform magnetic field B of0.3 T is along the positive Z-direction. A rectangular loop (abed) of sides 10cm×5cm carries a current I of 12 A. Out of the following different orientations which one corresponds to stable equilibrium?
View SolutionA rectangular loop of sides 20cm and 10cm carries a current of 5.0A. A uniform magnetic field of magnitude 2T exists parallel to the longer side of the loop. The torque acting on the loop is
View SolutionThe figure shows a current - carrying square loop ABCD of side 10 cm and current i=10A . The magnetic moment →M of the loop is
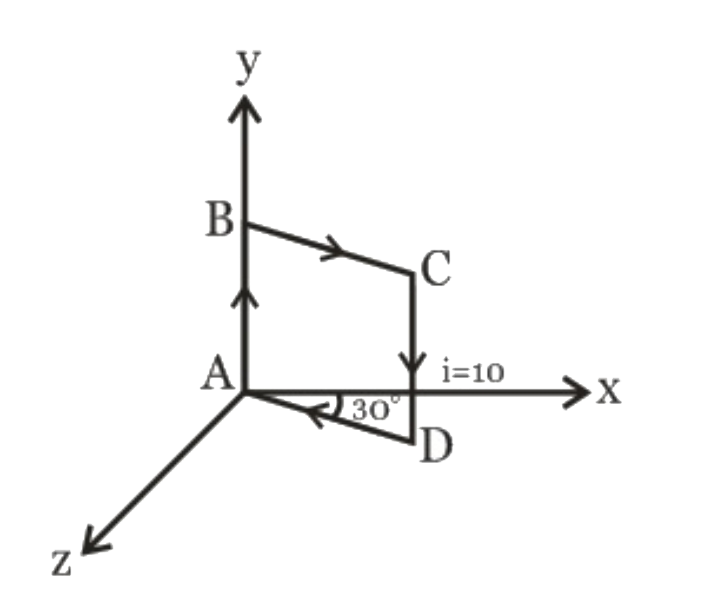 View Solution
View SolutionA long straight wire is carrying a current of 25 A. A square loop of side length 10 cm carrying a current of 15 A, is placed 2 cm from the wire as shown in figure. The force on the loop is
 View Solution
View Solution

