A uniform magnetic flux density of 0.1Wbm−2 extends over a plane circuit of area 1m2 and is normal to it. How quickly must the field be reduced to zero if an emf of 100 volt is to be induced in the circuit?
To solve the problem, we will use Faraday's law of electromagnetic induction, which states that the induced electromotive force (emf) in a circuit is equal to the negative rate of change of magnetic flux through the circuit.
1. Identify the Given Values:
- Magnetic flux density, B=0.1Wb/m2
- Area of the circuit, A=1m2
- Induced emf, E=100V
2. Calculate the Initial Magnetic Flux:
The magnetic flux (Φ) through the circuit is given by:
Φ=B⋅A
Substituting the values:
Φ=0.1Wb/m2×1m2=0.1Wb
3. Determine the Change in Magnetic Flux:
Since we want to reduce the magnetic field to zero, the change in magnetic flux (ΔΦ) is:
ΔΦ=Φfinal−Φinitial=0−0.1Wb=−0.1Wb
4. Apply Faraday's Law:
According to Faraday's law, the induced emf is given by:
E=−ΔΦΔt
Rearranging this gives:
Δt=−ΔΦE
5. Substitute the Values:
Substituting the values we have:
Δt=−−0.1Wb100V=0.1100=0.001s
6. Final Answer:
Therefore, the time required to reduce the magnetic field to zero in order to induce an emf of 100 volts is:
Δt=0.001s=10−3s
- Magnetic flux density, B=0.1Wb/m2
- Area of the circuit, A=1m2
- Induced emf, E=100V
The magnetic flux (Φ) through the circuit is given by:
Φ=B⋅A
Substituting the values:
Φ=0.1Wb/m2×1m2=0.1Wb
Since we want to reduce the magnetic field to zero, the change in magnetic flux (ΔΦ) is:
ΔΦ=Φfinal−Φinitial=0−0.1Wb=−0.1Wb
According to Faraday's law, the induced emf is given by:
E=−ΔΦΔt
Rearranging this gives:
Δt=−ΔΦE
Substituting the values we have:
Δt=−−0.1Wb100V=0.1100=0.001s
Therefore, the time required to reduce the magnetic field to zero in order to induce an emf of 100 volts is:
Δt=0.001s=10−3s
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Problems (Level-II)14videos
ELECTROMAGNETIC INDUCTION
- BOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Additional Exercise11videos
ELECTROMAGNETIC INDUCTION
- BOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercise (Very Short Answer Questions)33videos
ELECTROMAGNETIC INDUCTION
- BOOK - AAKASH SERIESCHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - PROBLEMS (LEVEL-II)26videos
ELECTRIC FIELD AND POTENTIAL
- BOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - EXERCISE -II22videos
ELECTROMAGNETIC WAVES
Similar Questions
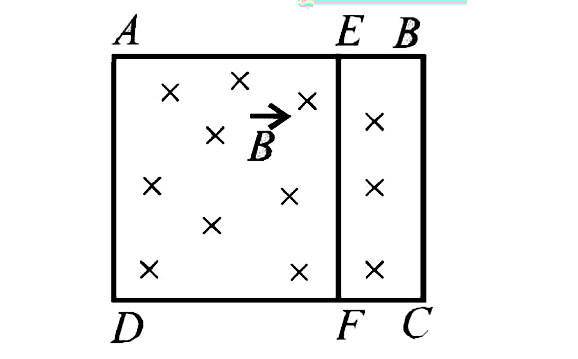
A rectangular frame ABCD, made of a uniform metal wire, has a straight connection between E and F made of the samae wire, as shown in fig. AEFD is a square of side 1m, and EB=FC=0.5m. The entire circuit is placed in steadily increasing, uniform magnetic field directed into the plane of the paper and normal to it. The rate of change of the magnetic field is 1T/s. The resistance per unit length of the wire is 1ω/m. Find the magnitude and directions of the currents in the segments AE, BE and EF.
 View Solution
View SolutionA magnetising field of 1500Am produces a magnetic flux density of 0.48Wb/m2 in a iron bar . Calculate permeability of iron bar used .
View Solution
Knowledge Check
- Question 1 - Select One
A coil of area 0.4m2 has 100 turns. A magnetic field of 0.04 Wb m−2 is acting normal to the coil surface. If this magnetic field is reduced to zero in 0.01 s, then the induced emf in the coil is
A160VB250 VC270 VD320 V - Question 2 - Select One
A circuit consists of a resistance 10 ohm and a capacitance of 0.1μF If an alternating e.m.f. of 100 V. 50 Hz is applied, calculate the current in the circuit.
A3.14mAB6.28mAC1.51mAD7.36mA
A coil of wire enclosing an area of 100cm2 is placed at an angle of 70∘ with a magnetic field B to 10−1Wbm−2. What is the flux through the coil? B is reduced to zero in 10−3sec. What e.m.f. is induced in the coil?
View SolutionCurrent in a circuit falls form 0.5 A to 0.0 A in 0.1 s. If an average e.m.f. of 200 V is induced, give an estimate of the self inductance of the circuit ?
View SolutionThe magnetic field perpendicular to the plane of a loop of area 0.1m2 is 0.2 T. Calculate the magnetic flux through the loop (in weber)
View SolutionA 800 turn coil of effective area 0.05m2 is kept perpendicular to a magnetic field 5×10−5 T. When the plane of the coil is rotated by 90∘ around any of its coplanar axis in 0.1 s, the emf induced in the coil will be:
View SolutionA magnetic field of 2×10−2T acts at right angles to a coil of area 100cm2 with 50 turns. The average emf induced in the coil is 0.1V, when it is removed from the field in time t. The value of t is
View SolutionA 0.5m long metal rod PQ completes the circuit as shown in the figure. The area of the circuit is perpendicular to the magnetic field of flux density 0.15T. If the resistance of the total circuit is 3Ω calculate the force needed to move the rod in the direction as indicated with a constant speed of 2ms−1
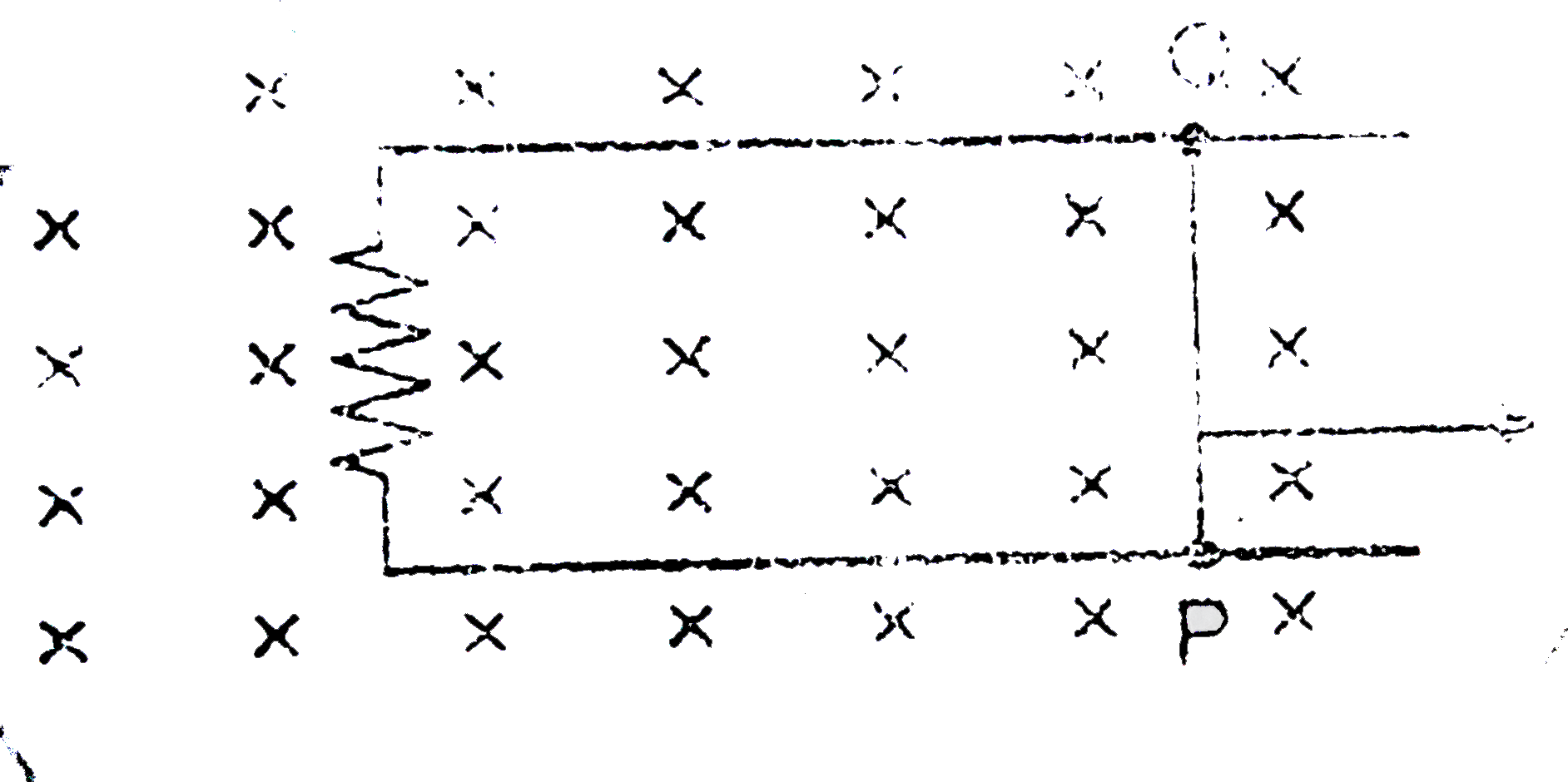 View Solution
View Solution

