A uniform metal disck of radius R is taken and out of it a disc of diameter R is cut-off from the end. The center of mass of the remaining part will be
R4 from the center
R3 from the center
R5 from the center
R6 from the center.
The correct Answer is:D
To find the center of mass of the remaining part of a uniform metal disc after cutting out a smaller disc, we can follow these steps:
1. Identify the Geometry:
- We have a uniform metal disc of radius R.
- A smaller disc of diameter R (which means its radius is R2) is cut out from the edge of the larger disc.
2. Determine the Area of the Discs:
- The area A1 of the larger disc (radius R) is given by:
A1=πR2
- The area A2 of the smaller disc (radius R2) is:
A2=π(R2)2=πR24
3. Calculate the Area of the Remaining Part:
- The area of the remaining part A is:
A=A1−A2=πR2−πR24=πR2(1−14)=πR2⋅34=3πR24
4. Locate the Center of Mass of the Larger Disc:
- The center of mass of the larger disc is at its center, which we can denote as point O (0, 0).
5. Locate the Center of Mass of the Smaller Disc:
- The center of mass of the smaller disc (cut-out) is at a distance R from the center of the larger disc along the radius, which we can denote as point C2 (R, 0).
6. Apply the Center of Mass Formula:
- We will use the formula for the center of mass of the remaining part:
A1x1−A2x2=Ax
- Where:
- x1=0 (center of the larger disc)
- x2=R (center of the smaller disc)
- A=3πR24 (area of the remaining part)
- Plugging in the values:
πR2⋅0−πR24⋅R=3πR24⋅x
- This simplifies to:
−πR34=3πR24⋅x
7. Solve for x:
- Dividing both sides by 3πR24:
x=−R3
8. Interpret the Result:
- The negative sign indicates that the center of mass of the remaining part is located R3 units to the left of the center of the original disc.
Final Answer:
The center of mass of the remaining part of the disc is located at a distance R3 from the center of the original disc towards the side from which the smaller disc was cut.
---
- We have a uniform metal disc of radius R.
- A smaller disc of diameter R (which means its radius is R2) is cut out from the edge of the larger disc.
- The area A1 of the larger disc (radius R) is given by:
A1=πR2
- The area A2 of the smaller disc (radius R2) is:
A2=π(R2)2=πR24
- The area of the remaining part A is:
A=A1−A2=πR2−πR24=πR2(1−14)=πR2⋅34=3πR24
- The center of mass of the larger disc is at its center, which we can denote as point O (0, 0).
- The center of mass of the smaller disc (cut-out) is at a distance R from the center of the larger disc along the radius, which we can denote as point C2 (R, 0).
- We will use the formula for the center of mass of the remaining part:
A1x1−A2x2=Ax
- Where:
- x1=0 (center of the larger disc)
- x2=R (center of the smaller disc)
- A=3πR24 (area of the remaining part)
- Plugging in the values:
πR2⋅0−πR24⋅R=3πR24⋅x
- This simplifies to:
−πR34=3πR24⋅x
- Dividing both sides by 3πR24:
x=−R3
- The negative sign indicates that the center of mass of the remaining part is located R3 units to the left of the center of the original disc.
The center of mass of the remaining part of the disc is located at a distance R3 from the center of the original disc towards the side from which the smaller disc was cut.
Topper's Solved these Questions
- CENTRE OF MASSBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Taking it together
73 Videos
- CENTRE OF MASSBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Assertion and reason
21 Videos
- CENTRE OF MASSBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Medical entrances gallery
27 Videos
- CALORIMETRY AND HEAT TRANSFERBOOK - DC PANDEY ENGLISHCHAPTER - CALORIMETRY AND HEAT TRANSFEREXERCISE - Medical entrance s gallery
38 Videos
- CENTRE OF MASS, IMPULSE AND MOMENTUMBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - Comprehension type questions
15 Videos
Similar Questions
From a circular disc of radius R and mass 9 M , a small disc of radius R/3 is removed from the disc. The moment of inertia of the remaining disc about an axis perpendicular to the plane of the disc and passing through O is
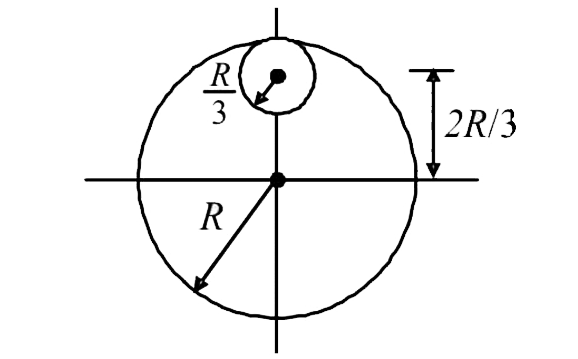
View SolutionA disc of radius r is cut from a larger disc of radius 4r in such a way that the edge of the hole touches the edge of the disc. The centre of mass of the residual disc will be a distance from centre of larger disc :-
View SolutionA disc of radius r is cut from a larger disc of radius 4r in such a way that the edge of the hole touches the edge of the disc. The centre of mass of the residual disc will be a distance from centre of larger disc :-
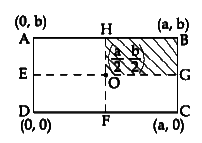
View SolutionA uniform rectangular thin sheet ABCD of mass M has length a and breadth b, as shown in the figure. If the shaded portion HBGO is cut-off, the coordinates of the center of mass of the remaining portion will be:
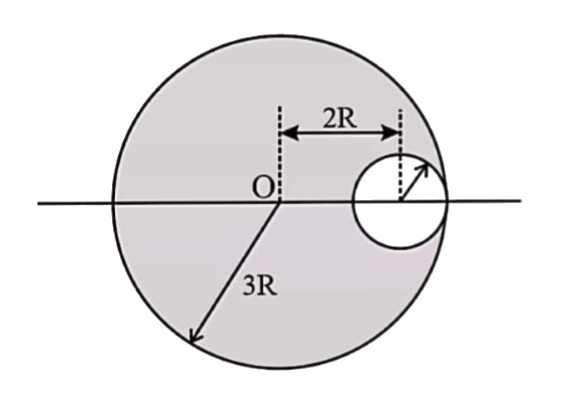
View SolutionThe figure shows a disc of radius 3R from which a circular hole of radius R is cut as shown in the figure. The distance of the centre of mass of the remaining object from the point O is
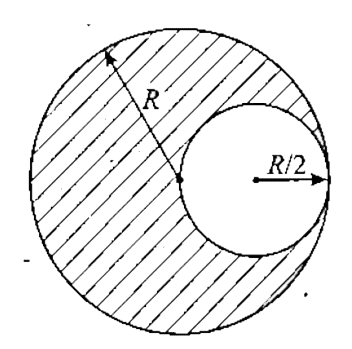
View SolutionFrom a circular disc of radius R, a square is cut out with a radius as its diagonal. The center of mass of remaining portion is at a distance from the center)
View SolutionFrom a circular disc of radius R a square is cut out with a radius as its diagonal . The distane of the centre of mass of the remainder from the centre of the disc is
View SolutionFrom the circular disc of radius 4R two small discs of radius R are cut off. The centre of mass of the new structure will be at
View SolutionThe moment of inertia of a uniform flat disc about its own axis is I. The radius of the disc is a A section ABCD of the disc (as shown in figure) is cut off and separated. The moment of inertia of the remainin g part of the disc about the same axis will be
View SolutionA disc of radis R is cut out from a larger disc of radius 2R in such a way that the edge of the hole touches the edge of the disc. Locate the centre of mass of the residual disc.
View Solution
