From a circular disc of radius R, a square is cut out with a radius as its diagonal. The center of mass of remaining portion is at a distance from the center)
Rπ−2
Rπ
R2(2π−1)
R2
To solve the problem of finding the center of mass of the remaining portion of a circular disc after a square is cut out, we can follow these steps:
1. Understand the Geometry:
- We have a circular disc with radius R.
- A square is cut out from the circle such that the diagonal of the square equals the radius of the circle.
2. Calculate the Side Length of the Square:
- The diagonal d of the square is given by d=R.
- The relationship between the side length a of the square and its diagonal is given by d=a√2.
- Therefore, we can express the side length as:
a=R√2
3. Determine the Areas:
- The area of the circular disc, Ac, is:
Ac=πR2
- The area of the square, As, is:
As=a2=(R√2)2=R22
4. Calculate the Masses:
- Assuming a uniform mass per unit area σ:
- Mass of the circle, mc:
mc=Ac⋅σ=πR2σ
- Mass of the square, ms:
ms=As⋅σ=R22σ
5. Determine the Center of Mass Coordinates:
- The center of mass of the circle is at the origin (0, 0).
- The center of mass of the square, which is cut out, is located at (R2,0).
6. Apply the Center of Mass Formula:
- The x-coordinate of the center of mass of the remaining portion can be calculated using:
xcm=mc⋅xc−ms⋅xsmc−ms
- Substituting the values:
xcm=(πR2σ⋅0)−(R22σ⋅R2)πR2σ−R22σ
- Simplifying:
xcm=0−R34σ(π−12)R2σ
- Canceling σ and R2:
xcm=−R4π−12=−R4(π−12)
7. Calculate the Distance:
- The distance from the center to the center of mass of the remaining portion is:
d=|xcm|=R4(π−12)
Summary of the Result
The distance of the center of mass of the remaining portion from the center of the circular disc is:
d=R4(π−12)
- We have a circular disc with radius R.
- A square is cut out from the circle such that the diagonal of the square equals the radius of the circle.
- The diagonal d of the square is given by d=R.
- The relationship between the side length a of the square and its diagonal is given by d=a√2.
- Therefore, we can express the side length as:
a=R√2
- The area of the circular disc, Ac, is:
Ac=πR2
- The area of the square, As, is:
As=a2=(R√2)2=R22
- Assuming a uniform mass per unit area σ:
- Mass of the circle, mc:
mc=Ac⋅σ=πR2σ
- Mass of the square, ms:
ms=As⋅σ=R22σ
- The center of mass of the circle is at the origin (0, 0).
- The center of mass of the square, which is cut out, is located at (R2,0).
- The x-coordinate of the center of mass of the remaining portion can be calculated using:
xcm=mc⋅xc−ms⋅xsmc−ms
- Substituting the values:
xcm=(πR2σ⋅0)−(R22σ⋅R2)πR2σ−R22σ
- Simplifying:
xcm=0−R34σ(π−12)R2σ
- Canceling σ and R2:
xcm=−R4π−12=−R4(π−12)
- The distance from the center to the center of mass of the remaining portion is:
d=|xcm|=R4(π−12)
The distance of the center of mass of the remaining portion from the center of the circular disc is:
d=R4(π−12)
Topper's Solved these Questions
- CENTRE OF MASS, IMPULSE AND MOMENTUMBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - Only one option is correct for JEE Advanced
60 Videos
- CENTRE OF MASS, IMPULSE AND MOMENTUMBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - More a than one option is Correct
1 Videos
- CENTRE OF MASSBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Medical entrances gallery
27 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 2 Subjective
21 Videos
Similar Questions
From the circular disc of radius 4R two small discs of radius R are cut off. The centre of mass of the new structure will be at

View SolutionA circular disc of radius R is removed from a bigger circular disc of radius 2R such that the circumferences of the discs coincide. The center of mass of new disc is αR from the center of the bigger disc. The value of α is
View Solution
Knowledge Check
From a uniform circular disc of radius R and mass 9M, a small disc of radius R3 is removed as shown in the figure. The moment of inertia of the remaining disc about an axis perpendicular to the plane of the disc and passing through centre of disc is :
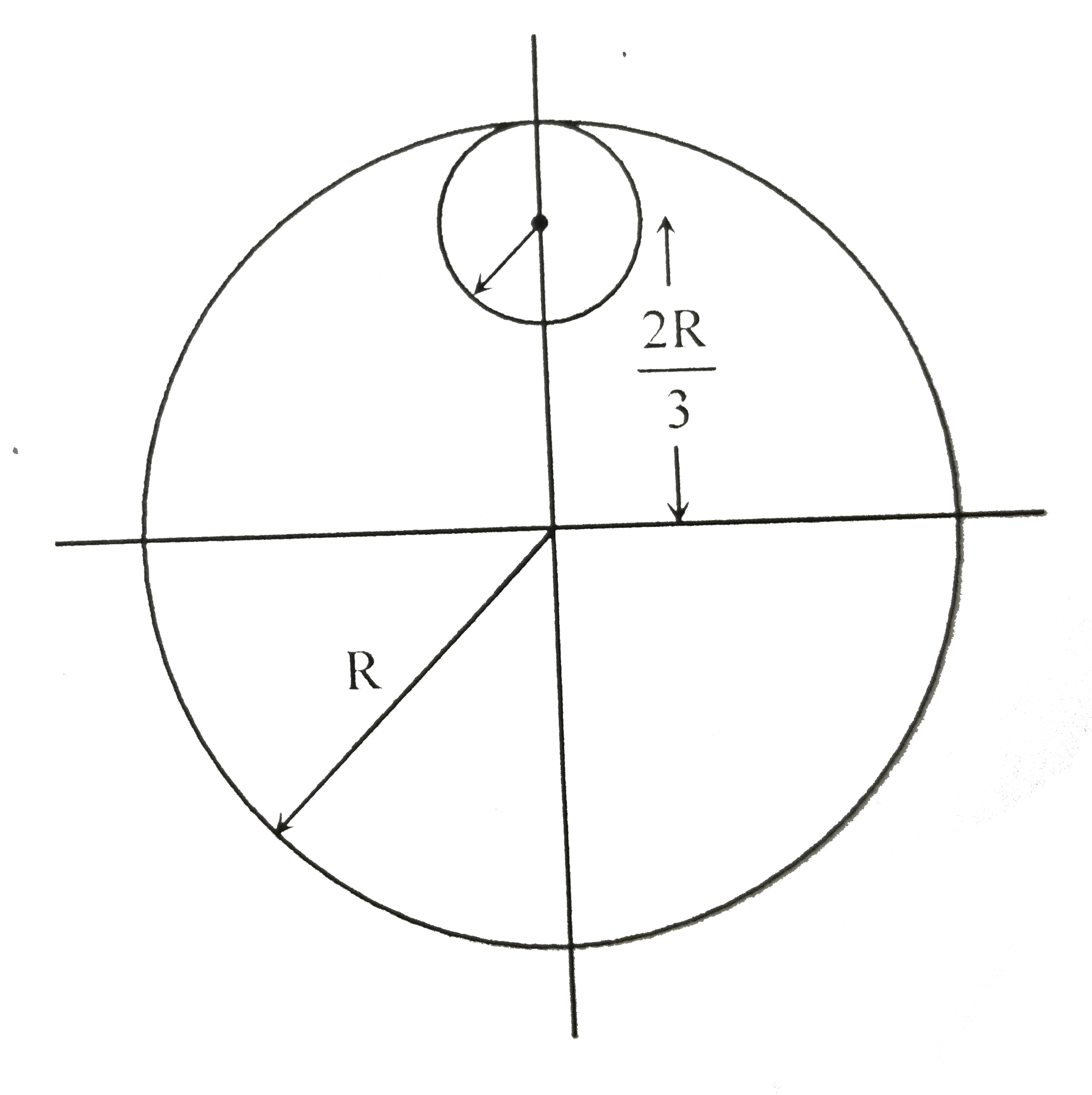 A4MR2B409MR2C40MR2D379MR2
A4MR2B409MR2C40MR2D379MR2
From a circular disc of mass M and radius R, a part of 60∘ is removed. The M.I. of the remaining portion of disc about an axis passing through the center and perpendicular to plane of disc is

View SolutionFrom a circular disc of radius R, a triangular portion is cut (sec figure). The distance of the centre of mass of the remainder from the centre of the disc is −

View SolutionFrom a uniform circular disc of mass M and radius R a small circular disc of radius R/2 is removed in such a way that both have a common tangent. Find the distance of centre of mass of remaining part from the centre of original disc.
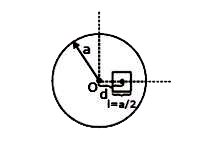
View SolutionA square shaped hole of side l=a2 is carved out at a distance d=a2 from the centre 'O' of a uniform circular disk of radius a. If the distance of the centre of mass of the remaining portion from O is −ax value of X (to the nearest integer) is _________.
View SolutionA square of side a2 is removed from a disc having radius a . Find centre of mass of remaing portion.

View SolutionFrom a circular disc of radius R and mass 9 M , a small disc of radius R/3 is removed from the disc. The moment of inertia of the remaining disc about an axis perpendicular to the plane of the disc and passing through O is

View SolutionFind the position of center of mass of the uniform lamina shown in figure, if small disc of radius α2 is cut from disc of radius a.
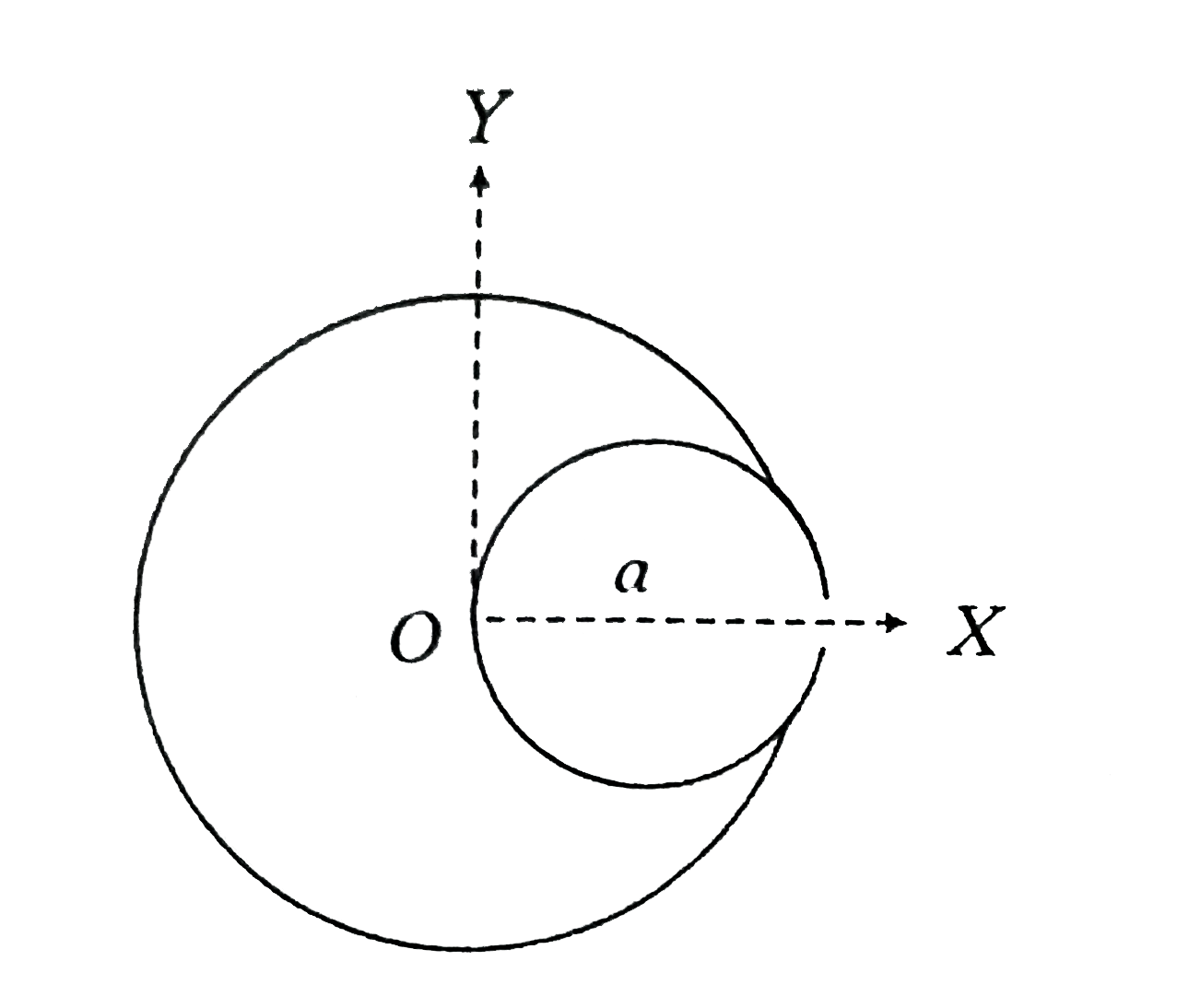
View Solution
