A uniform metre rod is bent into L shape with the bent arms at 90∘ to each other. The distance of the centre of mass from the bent point is
on the bisector of the angle, (1√2)m from vertex
on the bisector of angle, (12√2)m from vertex
on the bisector of the angle, 1/2 m from vertex
on the bisector of the angle, (14√2)m from vertex
The correct Answer is:D
To find the distance of the center of mass from the bent point of a uniform meter rod bent into an 'L' shape, we can follow these steps:
Step 1: Understand the Configuration
The uniform meter rod is bent into an 'L' shape, where each arm of the 'L' is 0.5 meters long (since the total length of the rod is 1 meter).
Step 2: Identify the Center of Mass of Each Arm
1. Horizontal Arm: The center of mass of the horizontal arm (0.5 m) is located at its midpoint, which is at (0.25 m, 0).
2. Vertical Arm: The center of mass of the vertical arm (0.5 m) is also at its midpoint, which is at (0, 0.25 m).
Step 3: Assign Masses
Assuming the mass of each half of the rod is m (since the rod is uniform), we have:
- Mass of the horizontal part, m1=m
- Mass of the vertical part, m2=m
Step 4: Calculate the Center of Mass of the Composite System
The coordinates of the center of mass (CM) can be calculated using the formula:
xCM=m1⋅x1+m2⋅x2m1+m2
yCM=m1⋅y1+m2⋅y2m1+m2
Substituting the values:
- For xCM:
xCM=m⋅0.25+m⋅0m+m=0.25m2m=0.252=18 m
- For yCM:
yCM=m⋅0+m⋅0.25m+m=0.25m2m=0.252=18 m
Step 5: Determine the Coordinates of the Center of Mass
The coordinates of the center of mass are:
(18,18)
Step 6: Calculate the Distance from the Bent Point
To find the distance d from the bent point (origin) to the center of mass, we use the Pythagorean theorem:
d=√x2CM+y2CM=√(18)2+(18)2=√164+164=√264=√132=14√2 m
Final Answer
The distance of the center of mass from the bent point is:
14√2 meters
---
The uniform meter rod is bent into an 'L' shape, where each arm of the 'L' is 0.5 meters long (since the total length of the rod is 1 meter).
1. Horizontal Arm: The center of mass of the horizontal arm (0.5 m) is located at its midpoint, which is at (0.25 m, 0).
2. Vertical Arm: The center of mass of the vertical arm (0.5 m) is also at its midpoint, which is at (0, 0.25 m).
Assuming the mass of each half of the rod is m (since the rod is uniform), we have:
- Mass of the horizontal part, m1=m
- Mass of the vertical part, m2=m
The coordinates of the center of mass (CM) can be calculated using the formula:
xCM=m1⋅x1+m2⋅x2m1+m2
yCM=m1⋅y1+m2⋅y2m1+m2
Substituting the values:
- For xCM:
xCM=m⋅0.25+m⋅0m+m=0.25m2m=0.252=18 m
- For yCM:
yCM=m⋅0+m⋅0.25m+m=0.25m2m=0.252=18 m
The coordinates of the center of mass are:
(18,18)
To find the distance d from the bent point (origin) to the center of mass, we use the Pythagorean theorem:
d=√x2CM+y2CM=√(18)2+(18)2=√164+164=√264=√132=14√2 m
The distance of the center of mass from the bent point is:
14√2 meters
Topper's Solved these Questions
- CENTRE OF MASSBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Taking it together
73 Videos
- CENTRE OF MASSBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Assertion and reason
21 Videos
- CENTRE OF MASSBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Medical entrances gallery
27 Videos
- CALORIMETRY AND HEAT TRANSFERBOOK - DC PANDEY ENGLISHCHAPTER - CALORIMETRY AND HEAT TRANSFEREXERCISE - Medical entrance s gallery
38 Videos
- CENTRE OF MASS, IMPULSE AND MOMENTUMBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - Comprehension type questions
15 Videos
Similar Questions
The distance of the centre of mass of T-shaped uniform plate from O is :
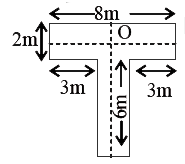
View SolutionA uniform wire of length l is bent into the shape of 'V' as shown. The distance of its centre of mass from the vertex A is :-

View SolutionA uniform thin rod is bent in the form of closed loop ABCDEFA as shown in the figure. The y− coordinate of the centre of mass of the system is
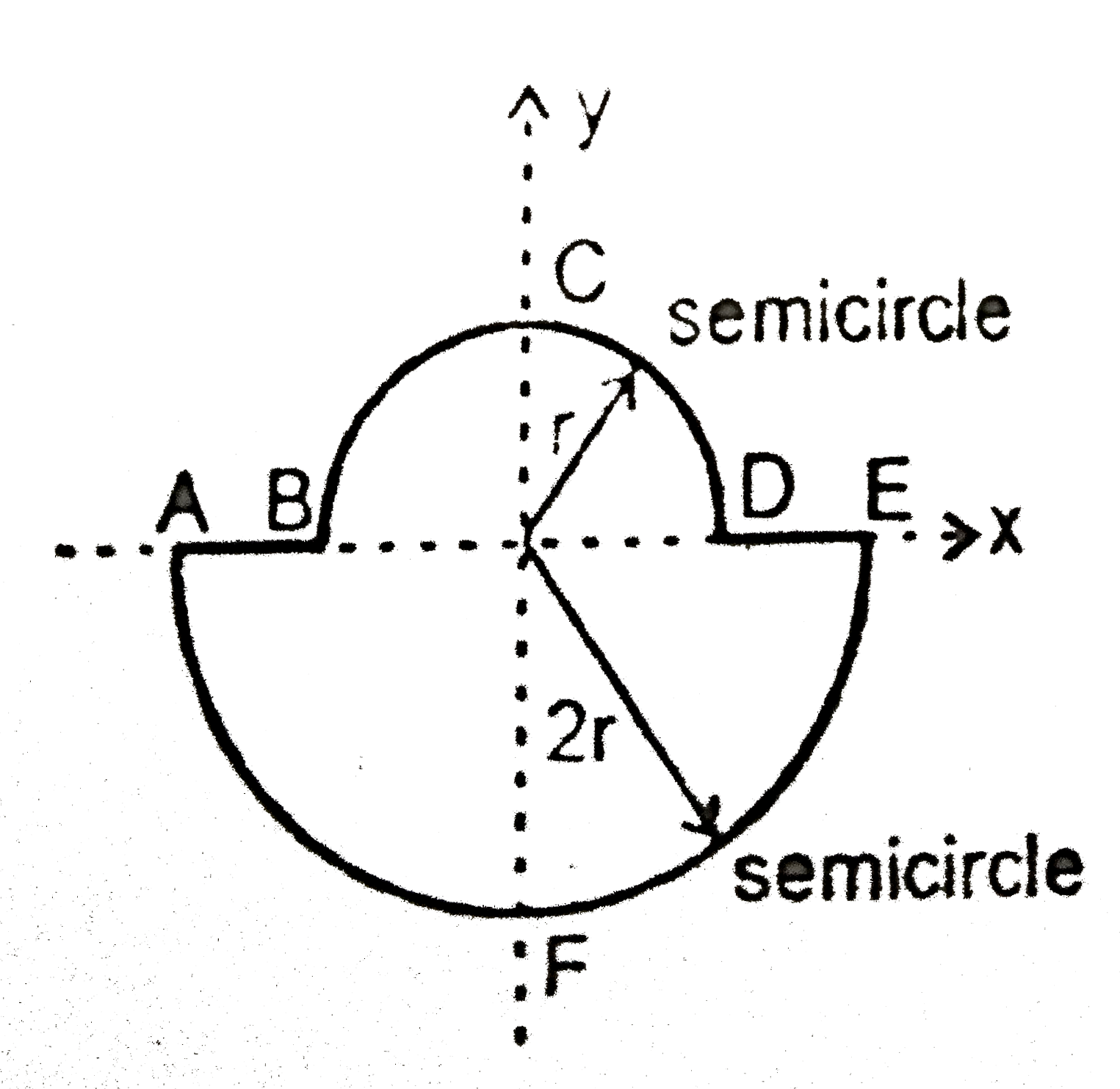
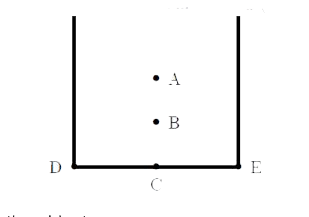
View SolutionA thick uniform wire is bent into the shape of the letter “U” as shown. Which point indicates the location of the center of mass of this wire?
View SolutionA sector cut from a uniform disk of radius 12cm and a uniform rod of the same mass bent into shape of an arc are arranged facing each other as shown in the figure. If center of mass of the combination is at the origin, what is the raius of the arc?
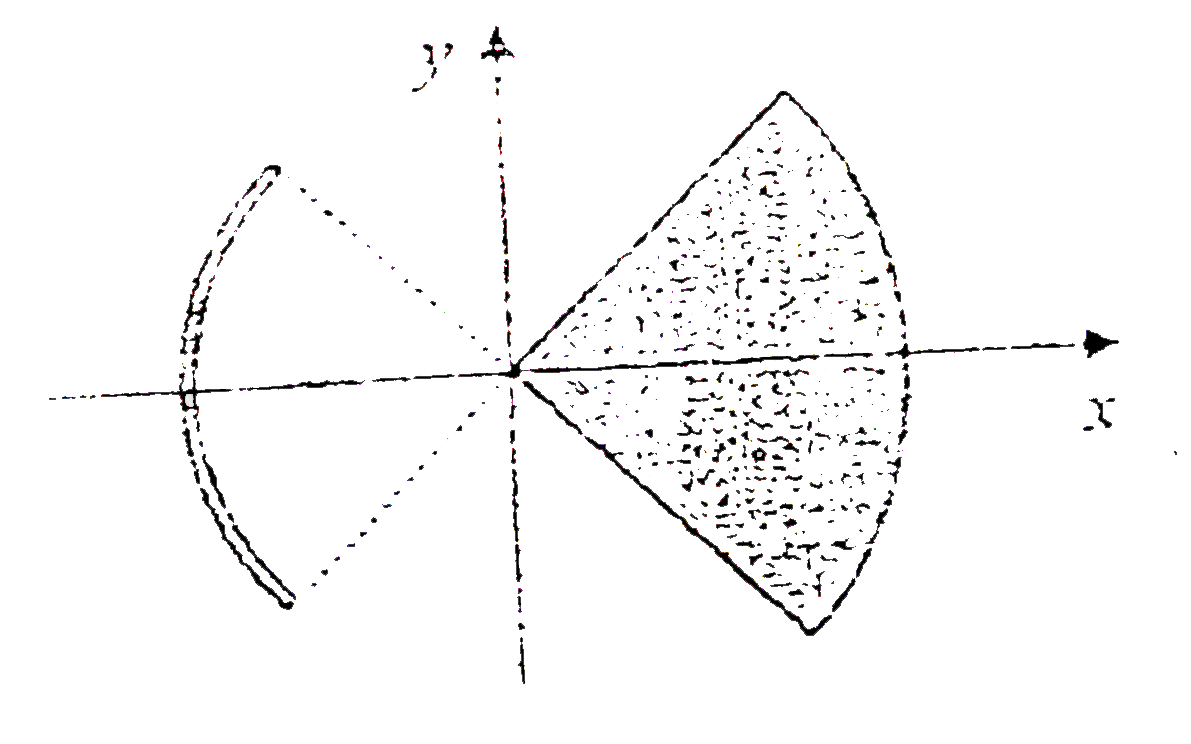
View SolutionTwo uniform thin rods each of length L and mass m are joined as shown in the figure. Find the distance of centre of mass the system from point O

View SolutionA thin uniform wire is bent to form the two equal sides AB and AC of triangle ABC, where AB=AC=5 cm. The third side BC, of length 6cm, is made from uniform wire of twice the density of the first. The distance of centre of mass from A is :
View SolutionA non–uniform thin rod of length L is placed along x-axis as such its one of ends at the origin. The linear mass density of rod is λ=λ0x. The distance of centre of mass of rod from the origin is :
View SolutionA thin wire of length L and uniform linear mass density ρ is bent into a circular loop with centre at O as shown. The moment of inertia of the loop about the axis XX' is
View SolutionThe objects in the figure are constructed of uniform wire bent into the shape shown. Find the position of the position of the centre of mass of each shape.

View Solution
