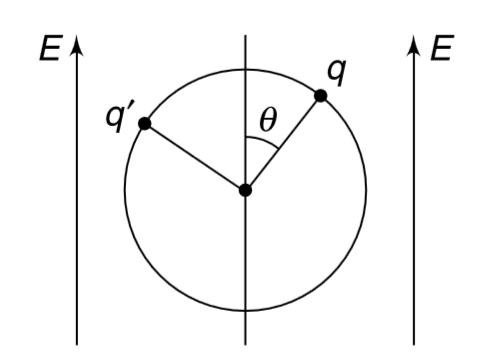
A uniform non conducting ring has mass m and radius R. tow point charges q and q' are fixed on its circumference at a separation of √2R the ring remains in equilibrium in air with its plane vertical in a region where exists a uniform vertically upward electric field E. Given E=4mg7q
(a) Find angle θ in equilibrium position (see figure). (b) The ring is given a small rotation in the plane of the figure and released. Will it perform oscillations?
The correct Answer is:(a). θ=tan−1(34)
(b). Yes
Topper's Solved these Questions
- ELECTROSTATICSBOOK - ARIHANTCHAPTER - ELECTROSTATICSEXERCISE - Level 3
59 Videos
- ELECTROSTATICSBOOK - ARIHANTCHAPTER - ELECTROSTATICSEXERCISE - Level 3
59 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - ARIHANTCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Level 3
12 Videos
- GEOMETRICAL OPTICSBOOK - ARIHANTCHAPTER - GEOMETRICAL OPTICSEXERCISE - Level 3
9 Videos
Similar Questions
Three small equally charged identical conducting balls are suspended from identical insulating threads secured at one point. Length (L) of the threads is large compared to the equilibrium separation (a) between any two balls. (a) One of the balls is suddenly discharged. Find the separation between the charged balls when equilibrium is restored. Assume that the threads do not interfere and balls do not collide. (b) If two of the balls are suddenly discharged, how will the balls behave after this? Find the separation between the balls when equilibrium is restored. The threads do not interfere
View SolutionThree small equally charged identical conducting balls are suspended from identical insulating threads secured at one point. Length (L) of the threads is large compared to the equilibrium separation (a) between any two balls. (a) One of the balls is suddenly discharged. Find the separation between the charged balls when equilibrium is restored. Assume that the threads do not interfere and balls do not collide. (b) If two of the balls are suddenly discharged, how will the balls behave after this? Find the separation between the balls when equilibrium is restored. The threads do not interfere
View SolutionA short bar magnet having magnetic dipole moment M is moving along the axis of a fixed conducting (non magnetic) ring of radius R. The axis of the ring is along z direction.
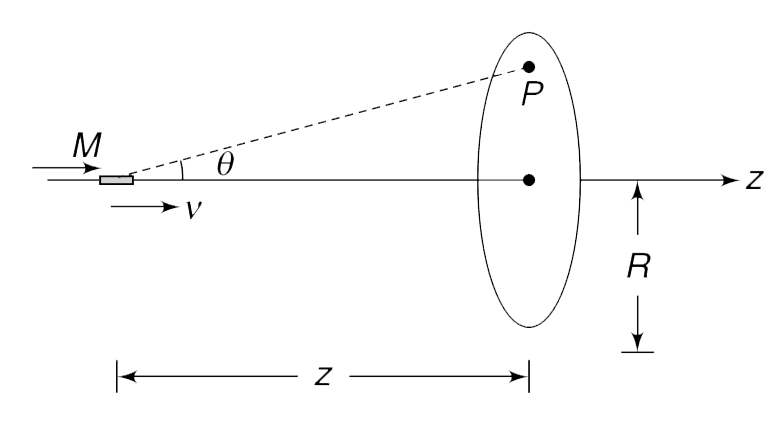
(a) Write the z component of magnetic field due to the magnetic dipole at a point P in the plane of the ring, at the instant the magnet is at a distance z from the centre of the ring. Position of point P can be defined in terms of angle θ as shown.
(b) Write the magnetic flux through the ring due to the magnetic field produced by the magnet as a function of z.
(c) Write the magnitude of emf induced in the ring at the instant shown if speed of the magnet at the moment is v.
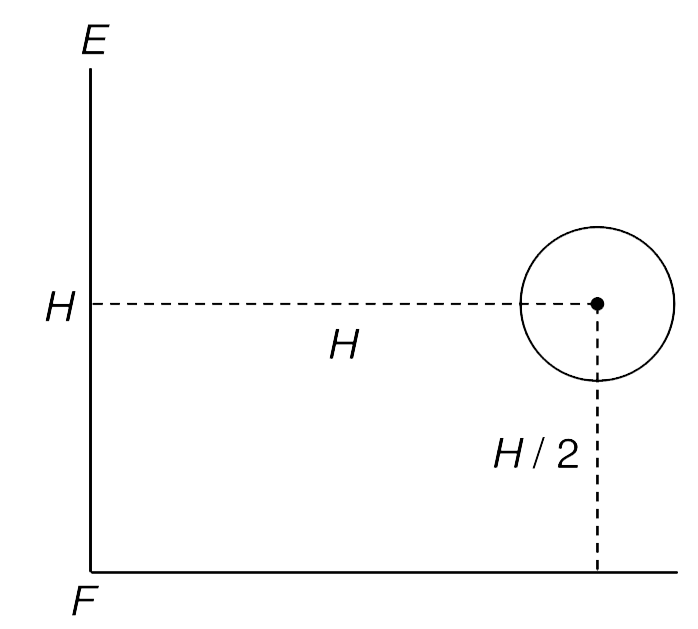
View SolutionIn the Figure FE is a man of height H standing on a floor. E is eye of the man and F is his foot. The distance between eye and the head is negligible. A steel ball of radius r is suspended in front of him. The distance of the ball from the man is H and height of the centre of the ball from the floor is H2. It is given that r<<H. The surface of the ball acts like a mirror and the man sees his image in it. Calculate the angle subtended by the image at the eye of the man.
View SolutionTwo point charge +q and -q are fixed on diameterically opposite point on the unirom ring, such that -q is at bottom and is contact will a perfect insulator incline plane. Total mass is equal to m remains in equilibrium on the rough inclined plane in the presence of uniform vertical electric field. Then
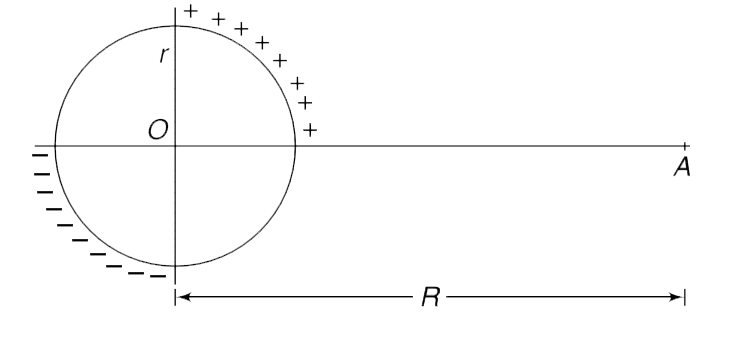
View SolutionA ring of radius r has a uniformly spread charge + q on quarter of its circumference. The opposite quarter of the ring carries a charge – q uniformly spread over it. Find the electric potential at a point A shown in the figure. Point A is at a distance R(gtgt r) from the centre of the ring.
View SolutionA uniform circular ring of radius R, mass m has uniformly distributed charge q. The ring is force to rotate about its own axis (which is vertical) without friction. In the space a uniform magnetic field B, directed vertically down ward exists in a cylindrical region. The cylindrical region is co-axial with B and has a radius greater than R. If B increasesa at a constant rate (dB)/(dt)=alpha . angular acceleration of the ring will.
View SolutionA ring with a uniform charge Q are radius R, is placed in the yz- plane with its centre at the origin. The field intensity at
View SolutionA wheel having mass m has charges +q and -q on diametrically opposite points. It remains in equilibrium on a rough inclined plane in the presence of a uniform vertical electric field E. The value of E is
View SolutionA wheel having mass m has charges +q and –q on diametrically opposite points. It remains in equilibrium on a rough inclined plane in the presence of uniform vertical electric field E =
View SolutionA thin conducting ring of radius R is given a charge +Q, Fig. The electric field at the center O of the ring due to the charge on the part AKB of the ring is E. The electric field at the center due to the charge on part ACDB of the ring is

View SolutionA thin conducting ring of radius R is given a charge +Q. The electric field at the centre O of the ring due to the charge on the part ABCD of the ring is
View SolutionA uniform thin ring of radius R and mass m suspended in a vertical plane from a point in its circumference. Its time period of oscillation is
View SolutionA uniform electric field vecE directed vertically upwards exists in a region of space. A point mass m carrying positive charge q is a state of equilibrium inside this electric field
View SolutionA thin conducting ring of radius R is given a charge +Q. The electric field at the centre o of the ring due to the charge on the part AKB of the ring is E. The electric field at the centre due to the charge on the part ACDB of the ring is
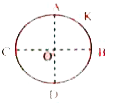
View Solution
