Question

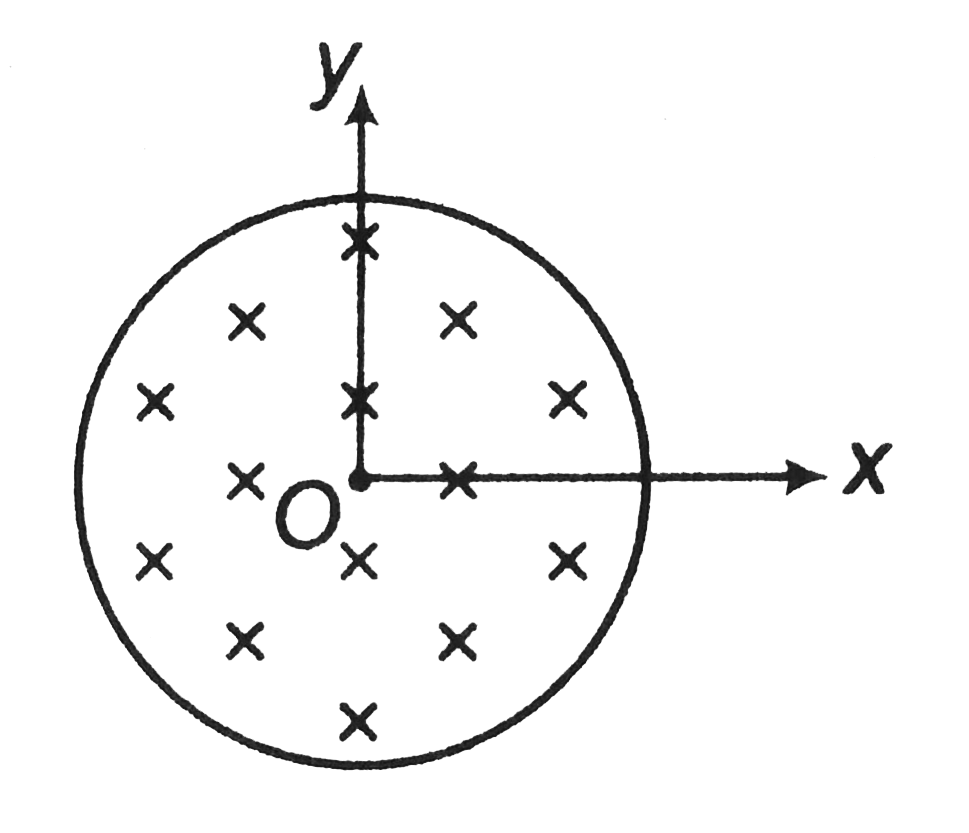
A uniform circular ring of radius R, mass m has uniformly distributed charge q. The ring is force to rotate about its own axis (which is vertical) without friction. In the space a uniform magnetic field B, directed vertically down ward exists in a cylindrical region. The cylindrical region is co-axial with B and has a radius greater than R. If B increasesa at a constant rate $\frac{dB}{dt}=\alpha$. angular acceleration of the ring will.

Options

A. Directly proportional to R
B. Directly proportional to q
C. Directly proportional to m
D. Independent of R and m

Answer

B

Explanation

To solve the problem step by step, we will analyze the situation involving a uniform circular ring with charge in a changing magnetic field.

Step 1: Understand the Setup
We have a uniform circular ring of radius \( R \), mass \( m \), and charge \( q \). The ring is rotating about its vertical axis in a uniform magnetic field \( B \), which is directed vertically downward. The magnetic field is increasing at a constant rate given by \( \frac{dB}{dt} = \alpha \).

Hint: Visualize the setup and identify the forces acting on the ring due to the changing magnetic field.

Step 2: Induced Electric Field
According to Faraday's law of electromagnetic induction, a changing magnetic field induces an electric field. The induced electric field \( E \) can be calculated using the formula:
\( E = -\frac{d\Phi}{dt} \)
where \( \Phi \) is the magnetic flux through the area of the ring.

The magnetic flux \( \Phi \) through the ring is given by:
\( \Phi = B \cdot A = B \cdot \pi R^2 \)
Since \( B \) is changing with time, we have:
\( \frac{d\Phi}{dt} = \pi R^2 \frac{dB}{dt} = \pi R^2 \alpha \)
Thus, the induced electric field \( E \) is:
\( E = -\frac{d\Phi}{dt} = -\pi R^2 \alpha \)

Hint: Remember that the induced electric field is related to the rate of change of magnetic flux.

Step 3: Calculate the Force on the Ring
The electric field induces a force on the charged ring. The linear charge density \( \lambda \) of the ring is given by:
\( \lambda = \frac{q}{2\pi R} \)
The total force \( F \) acting on the ring due to the induced electric field is:
\( F = \lambda \cdot E \cdot (2\pi R) = \left(\frac{q}{2\pi R}\right)(-\pi R^2 \alpha)(2\pi R) = -q R \alpha \)

Hint: Use the relationship between charge density, electric field, and the total force.

Step 4: Calculate the Torque
The torque \( \tau \) acting on the ring due to the force is given by:
\( \tau = R \cdot F = R \cdot (-q R \alpha) = -q R^2 \alpha \)

Hint: Torque is the product of the radius and the force acting at that radius.

Step 5: Relate Torque to Angular Acceleration
Using Newton's second law for rotation, we have:
\( \tau = I \cdot \alpha \)
where \( I \) is the moment of inertia of the ring. The moment of inertia \( I \) of a ring about its axis is:
\( I = m R^2 \)
Setting the expressions for torque equal gives:
\( -q R^2 \alpha = m R^2 \cdot \alpha \)

Step 6: Solve for Angular Acceleration
We can now solve for the angular acceleration \( \alpha \):
\( -q R^2 \alpha = m R^2 \cdot \alpha \implies \alpha = \frac{-q \alpha}{m} \)
Thus, the angular acceleration of the ring is:
\( \alpha = \frac{q \alpha}{2m} \)

Hint: Make sure to keep track of the signs and understand the relationship between torque, moment of inertia, and angular acceleration.

Final Answer
The angular acceleration of the ring is given by:
\( \alpha = \frac{q \alpha}{2m} \)