A uniform of radius 5.0cm and mass 200g is fixed at its centre to a metal wire , the other end of which is fixed to a celling. The hanging disc is rotate about the wire through an angle and is released. If the disc makes torsional oscillations with time period 0.20s , find the torsional constant of the wire.

The situation is shown in figure . The moment of inertia of the about the wire is
l=mr22=(0.200kg)(5.0×10−2m)22
=2.5×10−4kg−m2
The time period is given by
T=2π√lkork=√4π2lT2
=4π2(2.5×10−4lg−m2)(0.20s)2=0.25kg−m2/s2
Topper's Solved these Questions
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Solved Example
15 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Exercise 4.1
23 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Interger
11 Videos
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Interger type
3 Videos
Similar Questions
A uniform of radius 5.0cm and mass 200g is fixed at its centre to a metal wire , the other end of which is fixed to a celling. The hanging disc is rotate about the wire through an angle and is released. If the disc makes torsional oscillations with time period 0.20s , find the torsional constant of the wire.

View SolutionA uniform disc of radius 5.0 cm and mass 200g is fixed at its centre to a metal wire, the other end of which is fixed with a clamp. The hanging disc is rotated about the wire through an angle and is released. If the disc makes torsional oscillations with time period 0.20s, find the torsional constant of the wire.
View Solution
Knowledge Check
A circular disc fixed at its centre to a metal wire and the other end of the wire is clamped. The disc is rotated about the wire as axis and is released. The disc about this axis makes simple harmonic oscillations with a frequency of 12Hz. If moment of inertia of the disc about this axis is 0.1 kg −m2, the torsional constant of the wire is
A0.99 kg m2s−2B0.45 kg m2s−2C09.9 kg m2s−2D0.49 kg m2s−2A metal rod of length 'L' and mass 'm' is piovted at one end. A thin disk of mass 'M' and radius 'R'(<L). Is attached at its centre to the free end of the rod. Consider two ways the disc is attached: (case A). The disc is not free to rotate about its centre and (case B) the disc is free to rotate about its center. The rod-disc sustem perform SHM in vertical plane after being released from the same displaced potion. Which of the following statement(s) is (are) true?
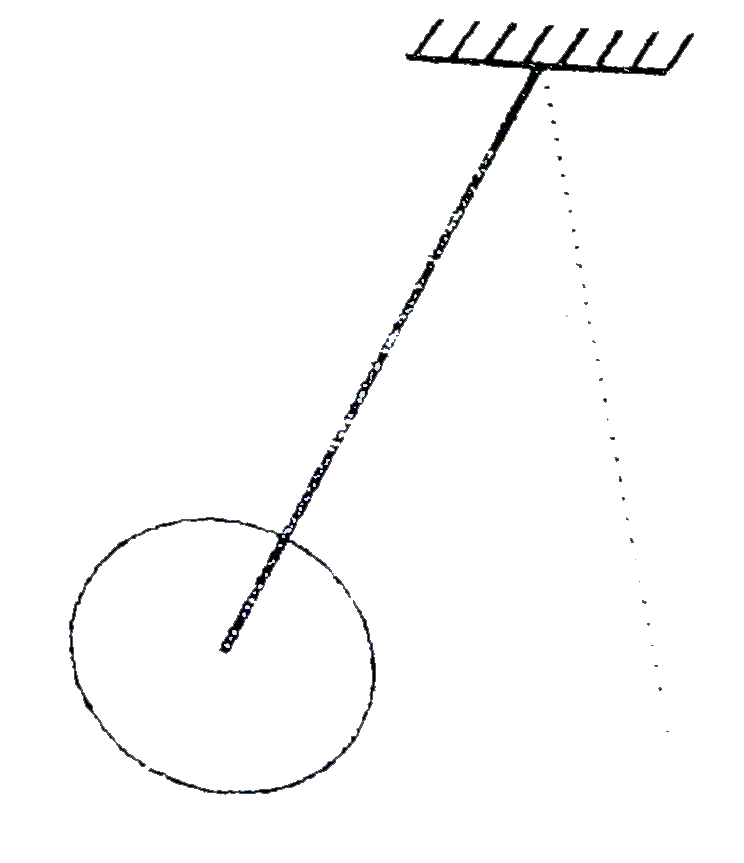 ARestoring torque in case A = Restoring torque in caseBBRestoring torque in case A< Restoring torque in caseBCRestoring frequency case A> Angular frequency for caseBDRestoring frequency case A< Angular frequency for caseB
ARestoring torque in case A = Restoring torque in caseBBRestoring torque in case A< Restoring torque in caseBCRestoring frequency case A> Angular frequency for caseBDRestoring frequency case A< Angular frequency for caseB
(a) A uniform disc of radius 5⋅0cm and mass 200g is fixed at its centre to a metal wire, the other end of which is fixed with a clamp. The hanging disc is rotated about the wire through an angle and is released. If the disc makes torsional oscillations with time period 0.20s, find the torsional constant of the wire.
(b) In the previous part, another disc is placed over the first one and the time period of the system become 0.65. Find the M.I. of the second disc about the wire.
View SolutionA uniform disc of mass m and radius r is suspended through a wire attached to its centre. If the time period of the torsional oscillations be T, what is the torsional constant of the wire?
View SolutionA circular disc of mass 12 kg is suspended by a wire attached to its centre. The wire is twisted by rotating the disc and then released, so that the time period of torsional oscillation is 2 s. If the radius of the disc is 10 cm, then calculate the torsional spring constant of the wire.
View SolutionA circular disc of mass 10kg is suspended by a wire attahced to its centre. The wire is twisted by rotating the disc and released. The period of torsional oscillations is found to be 1.5s. The radius of the disc is 15cm. Determing the torsional spring constant of the wire. (Torsional spring constant α is definied by the relation J=−αθ, where J is the restoring coubple and θ the angle of twist.
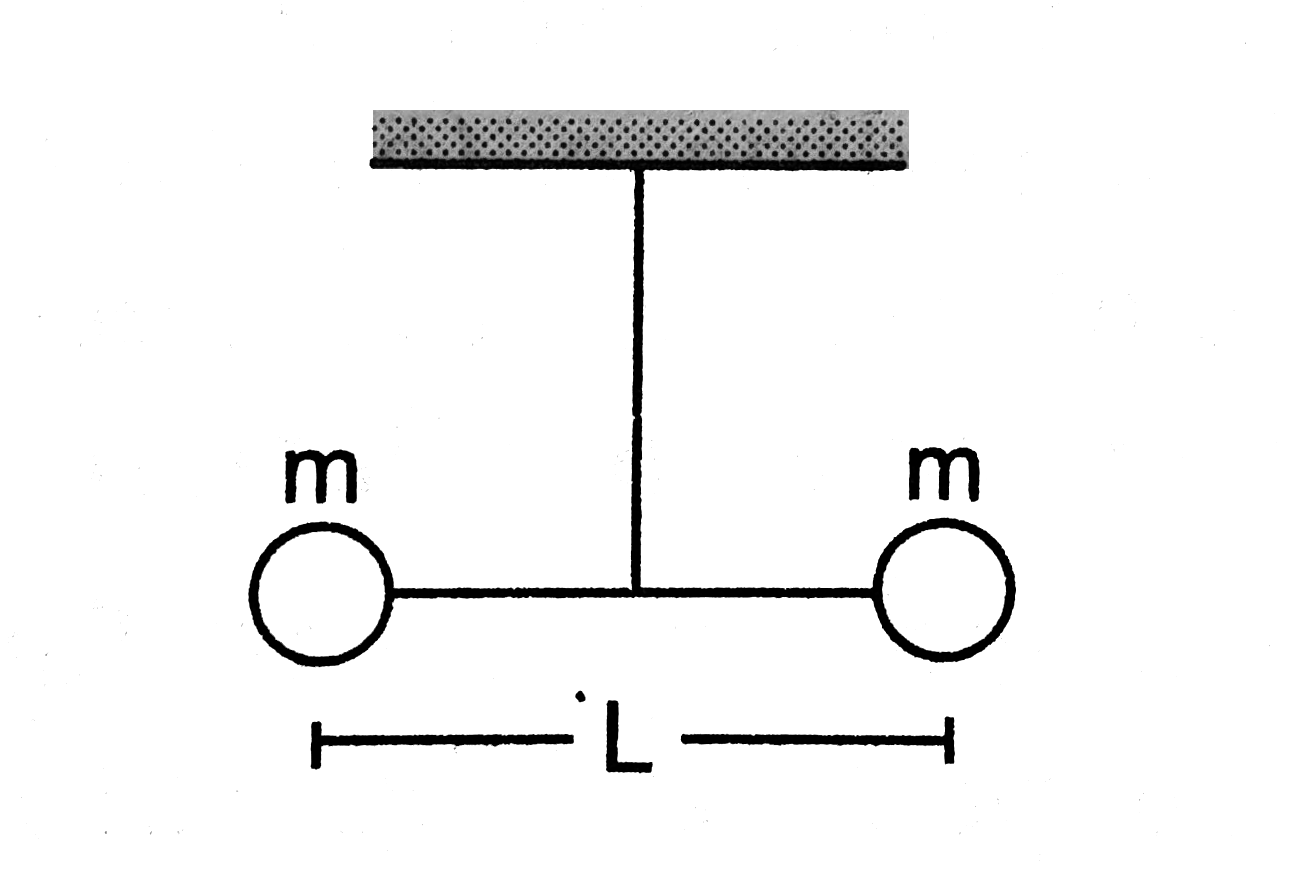
View SolutionTwo small balls, each of mass m are connected by a light rigid rod of length L. The system is suspended from its centre by a thin wire of torsional constant k. The rod is rotated about the wire through an angle θ0 and released. Find the tension in the rod as the system passes through the mean position.
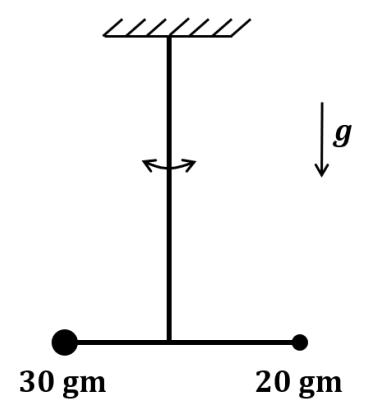
View SolutionTwo point-like objects of masses 20gm and 30gm are fixed at the two ends of a rigid massless rod of length 10cm. This system is suspended vertically from a rigid ceiling using a thin wire attached to its center of mass, as shown in the figure. The resulting torsional pendulum undergoes small oscillations. The torsional constant of the wire is 1.2×10−8Nmrad−1 . The angular frequency of the oscillations in n×10−3rads−1 . The value of n is _____.
View Solution
