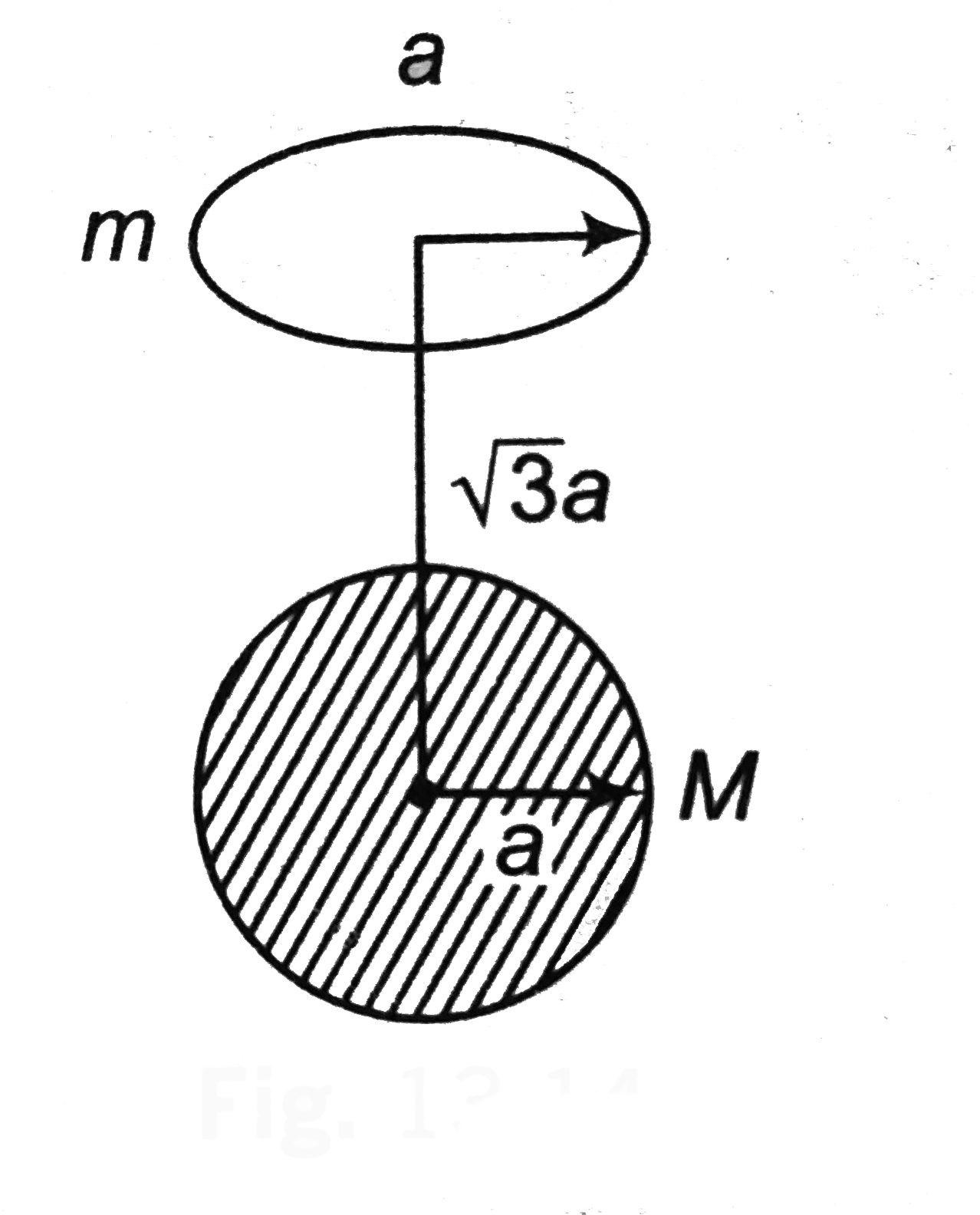
A uniform ring of mas m and radius a is placed directly above a uniform sphere of mass M and of equal radius. The centre of the ring is at a distance √3 a from the centre of the sphere. Find the gravitational force exerted by the sphere on the ring.
GMm8r2
GMm4r2
√3GMm8r2
GMm8r3√3
The correct Answer is:C
( c) dF=GMdm4r2
F=∑dFcosθ
=∑GMdm4r2cosθ
=GM4r2×√3r2r∑dm
=√3GMm8r2

Topper's Solved these Questions
- GRAVITATIONBOOK - NCERT FINGERTIPSCHAPTER - GRAVITATIONEXERCISE - NCERT Exemplar
8 Videos
- GRAVITATIONBOOK - NCERT FINGERTIPSCHAPTER - GRAVITATIONEXERCISE - Assertion And Reason
15 Videos
- GRAVITATIONBOOK - NCERT FINGERTIPSCHAPTER - GRAVITATIONEXERCISE - Miscellaneous Question
11 Videos
- KINETIC THEORYBOOK - NCERT FINGERTIPSCHAPTER - KINETIC THEORYEXERCISE - Assertion And Reason
10 Videos
Similar Questions
A uniform rig of mas m and radius a is placed directly above a uniform sphre of mass M and of equyal radius. The centre of the ring is at a distance √3 a from the centre of the sphere. Find the gravitational foerce exerted by the sphere on the ring.
View SolutionA uniform ring of mass 2m and radius a is placed directly above the uniform sphere of mass M and of same radius. The centre of ring is at distance √3a from the centre of sphere. The gravitational force exerted by the sphere on the ring is NGMma2 units. Calculate is the value of N?
View Solution
Knowledge Check
A uniform ring of mass M and radius R is placed directly above a uniform sphere of mass 8M and of same radius R. The centre of the ring is at a distance of d=√3R from the centre of the sphere. The gravitational attraction between the sphere and the ring is
AGM2R2B3GM22R3C2GM2√2R2D√3GM2R2A uniform ring of mass M and radius R is placed directly above a uniform sphere of mass 8M and of same radius R. The centre of the ring is at a distance of d=√3R from the centre of the sphere. The gravitational attraction between the sphere and the ring is
AGM2R2B3GM2R3C2GM2√2R2D√3GM2R2A uiform ring of mass M and radius R is placed directly above a uniform sphere of mass 8M and same radius R. The centre of the sphere. The gravitational atraction between the sphere and the ring is
A8GM2R2B2GM2√3R2C3GM22R2D√32GM2R2
A uniform ring of mass m is lying at a distance √3 a from the centre of mass M just over the sphere (where a is the radius of the ring as well as that of the sphere). Find the magnitude of gravitational force between them .
View SolutionFor a uniform ring of mass M and radius R at its centre
View SolutionThe figure represents a solid uniform sphere of mass M and radius R. A spherical cavity of radius r is at a distance a from the centre of the sphere. The gravitational field inside the cavity is

View SolutionThe gravitational field due to an uniform solid sphere of mass M and radius a at the centre of the sphere is
View SolutionInside a uniform sphere of density ρ there is a spherical cavity whose centre is at a distance l from the centre of the sphere. Find the strength of the gravitational field inside the cavity.
View Solution
