For a uniform ring of mass M and radius R at its centre
field and potential both are zero
field is zero but potential is
field is zero but potential is
magnitude of field is and potential
The correct Answer is:C
To solve the problem regarding the gravitational field and gravitational potential at the center of a uniform ring of mass M and radius R, we can follow these steps:
1. Understanding the Setup:
We have a uniform ring with mass M and radius R. We need to determine the gravitational field and gravitational potential at the center of this ring.
2. Gravitational Field Calculation:
- Consider an infinitesimal mass element dm on the ring. The gravitational field d→E due to this mass element at the center of the ring points towards the mass element.
- Now, consider another mass element dm located directly opposite to the first one on the ring. The gravitational field d→E′ due to this mass element will also point towards it but in the opposite direction.
- Since both mass elements are equidistant from the center and have the same mass dm, the magnitudes of the gravitational fields d→E and d→E′ will be equal, but their directions will be opposite.
3. Cancellation of Gravitational Fields:
- When we sum up the contributions of all such pairs of mass elements around the ring, we find that they will cancel each other out. Therefore, the net gravitational field →E at the center of the ring is:
→E=0
4. Gravitational Potential Calculation:
- The gravitational potential V due to a mass element dm at a distance R from the center is given by:
dV=−GdmR
- Since gravitational potential is a scalar quantity, we can sum the contributions from all mass elements without worrying about their directions. Thus, we integrate over the entire ring:
V=∫dV=∫−GdmR
- The total mass of the ring is M, so:
V=−GR∫dm=−GMR
5. Final Results:
- The gravitational field at the center of the ring is:
→E=0
- The gravitational potential at the center of the ring is:
V=−GMR
Conclusion:
The gravitational field at the center of a uniform ring is zero, and the gravitational potential at the center is −GMR.
We have a uniform ring with mass M and radius R. We need to determine the gravitational field and gravitational potential at the center of this ring.
- Consider an infinitesimal mass element dm on the ring. The gravitational field d→E due to this mass element at the center of the ring points towards the mass element.
- Now, consider another mass element dm located directly opposite to the first one on the ring. The gravitational field d→E′ due to this mass element will also point towards it but in the opposite direction.
- Since both mass elements are equidistant from the center and have the same mass dm, the magnitudes of the gravitational fields d→E and d→E′ will be equal, but their directions will be opposite.
- When we sum up the contributions of all such pairs of mass elements around the ring, we find that they will cancel each other out. Therefore, the net gravitational field →E at the center of the ring is:
→E=0
- The gravitational potential V due to a mass element dm at a distance R from the center is given by:
dV=−GdmR
- Since gravitational potential is a scalar quantity, we can sum the contributions from all mass elements without worrying about their directions. Thus, we integrate over the entire ring:
V=∫dV=∫−GdmR
- The total mass of the ring is M, so:
V=−GR∫dm=−GMR
- The gravitational field at the center of the ring is:
→E=0
- The gravitational potential at the center of the ring is:
V=−GMR
The gravitational field at the center of a uniform ring is zero, and the gravitational potential at the center is −GMR.
Topper's Solved these Questions
- GRAVITATIONBOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - Check Point 10.4
10 Videos
- GRAVITATIONBOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - Check Point 10.5
20 Videos
- GRAVITATIONBOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - Check Point 10.2
20 Videos
- GENERAL PHYSICSBOOK - DC PANDEYCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE
2 Videos
- KINEMATICSBOOK - DC PANDEYCHAPTER - KINEMATICSEXERCISE - INTEGER_TYPE
11 Videos
Similar Questions
Knowledge Check
The escape velocity form the centre of a unifrom ring of mass M and radius R is :
A√2GMRB√GMRC√GM2RD√GMRA uniform disc of mass M and radius R is hinged at its centre C. A force F is applied on the disc as shown. At this instant, the angular acceleration of the disc is
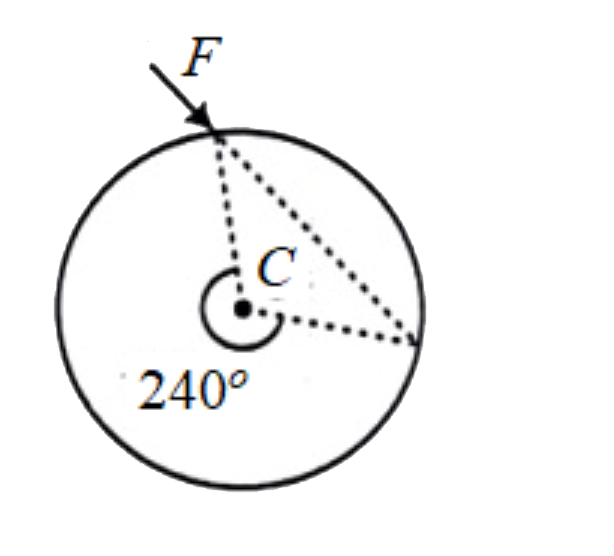 A√3FMRBFMRC2√3FMRDF2MR
A√3FMRBFMRC2√3FMRDF2MRA uniform ring of mass m and radius R is in uniform pure rolling motion on a horizontal surface. The velocity of the centre of ring is V0. The kinetic energy of the segment ABC is:
 AmV202−mV20πBmv202+mv20πCmv202Dmv20
AmV202−mV20πBmv202+mv20πCmv202Dmv20
Find the moment of inertia of a half uniform ring (mass m, radius r) about its center.
View SolutionA uniform disc of mass M and radius R is hinged at its centre C . A force F is applied on the disc as shown . At this instant , angular acceleration of the disc is

View SolutionMoment of inertia of a uniform circular ring of mass M and radius R about a diameter of ring is………………. .
View SolutionThe M.I. of a thin ring of mass M and radius R about an axis through the diameter in its plane will be:
View SolutionA uniform ring of mass M and radius R is placed directly above a uniform sphere of mass 8M and of same radius R. The centre of the ring is at a distance of d=√3R from the centre of the sphere. The gravitational attraction between the sphere and the ring is
View Solution