A uniform rod AB of length 2l and mass m is rotating in a horizontal plane about a vertical axis through A, with angular velocity ω, when the mid-point of the rod strikes a fixed nail and is brought immediately to rest. Find the impulse exerted by the nail.
To solve the problem, we need to find the impulse exerted by the nail when the midpoint of the rotating rod strikes it and comes to rest. Here's the step-by-step solution:
Step 1: Understand the Initial Conditions
The rod AB has a length of 2l and mass m. It is rotating about a vertical axis through point A with an angular velocity ω.
Hint: Identify the key parameters of the system: length, mass, and angular velocity.
Step 2: Determine the Moment of Inertia
The moment of inertia I of the rod about the end A (where it is rotating) can be calculated using the formula for a uniform rod:
I=13mL2
For our rod of length 2l:
I=13m(2l)2=4ml23
Hint: Remember that the moment of inertia depends on the axis of rotation and the mass distribution.
Step 3: Calculate Initial Angular Momentum
The initial angular momentum Li of the rod can be calculated as:
Li=I⋅ω=(4ml23)⋅ω=4ml2ω3
Hint: Angular momentum is the product of moment of inertia and angular velocity.
Step 4: Determine Final Angular Momentum
After the midpoint of the rod strikes the nail, the rod comes to rest. Therefore, the final angular momentum Lf is:
Lf=0
Hint: When the rod comes to rest, its angular momentum becomes zero.
Step 5: Calculate Change in Angular Momentum
The change in angular momentum ΔL can be calculated as:
ΔL=Lf−Li=0−4ml2ω3=−4ml2ω3
Hint: The change in angular momentum is the difference between final and initial angular momentum.
Step 6: Relate Angular Impulse to Linear Impulse
The impulse J exerted by the nail is related to the change in angular momentum by the following equation:
ΔL=J⋅r⊥
Where r⊥ is the perpendicular distance from the axis of rotation to the point where the impulse is applied. For our rod, this distance is l (the midpoint of the rod).
Hint: Understand how linear impulse relates to angular impulse through the distance from the axis of rotation.
Step 7: Solve for Impulse J
Substituting the values we have:
−4ml2ω3=J⋅l
Solving for J:
J=−4ml2ω3l=−4mlω3
The negative sign indicates that the impulse is in the opposite direction of the initial motion.
Hint: The impulse is a vector quantity; the direction matters.
Final Result
The magnitude of the impulse exerted by the nail is:
J=4mlω3
The rod AB has a length of 2l and mass m. It is rotating about a vertical axis through point A with an angular velocity ω.
The moment of inertia I of the rod about the end A (where it is rotating) can be calculated using the formula for a uniform rod:
The initial angular momentum Li of the rod can be calculated as:
After the midpoint of the rod strikes the nail, the rod comes to rest. Therefore, the final angular momentum Lf is:
The change in angular momentum ΔL can be calculated as:
The impulse J exerted by the nail is related to the change in angular momentum by the following equation:
Substituting the values we have:
The magnitude of the impulse exerted by the nail is:
Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 2 Single Correct
26 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 2 Multiple Correct
36 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 1 Objective
30 Videos
- ROTATIONBOOK - DC PANDEYCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises
39 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEYCHAPTER - ROTATIONAL MOTIONEXERCISE - Integer Type Questions
17 Videos
Similar Questions
A uniform of mass m and length L is tied to a vertical shaft. It rotates in horizontal plane about the vertical axis at angular velocity ω. How much horizontal force does the shaft exert on the rod?

View SolutionA conical pendulum, a thin uniform rod of length l and mass m, rotates uniformly about a vertical axis with angular velocity ω(the upper end of the rod is hinged). Find the angle θ between the rod and the vertical.
View Solution
Knowledge Check

A uniform rod of legth L is free to rotate in a vertica plane about a fixed horizontal axis through B. The rod begins rotating from rest. The angular velocity ω at angle θ is given asA√(6gL)sin(θ2)B√(6gL)cos(θ2)C√(6gL)sinθD√(6gL)cosθA rod is rotating with angular velocity ω about axis AB. Find cosθ.
 Ag2lω2Bglω2C2g(lω)2D3g2lω2
Ag2lω2Bglω2C2g(lω)2D3g2lω2A uniform rod of mass m and length l rotates in a horizontal plane with an angular velocity ω about a vertical axis passing through one end. The tension in the rod at a distance x from the axis is
A12mω2xB12mω2(1−x2l)C12mω2l(1−x2l2)D12mω2l[1−xl]
A uniform material rod of length L is rotated in a horizontal plane about a vertical axis through one of its ends. The angular speed of rotation is w. Find increase in length of the rod. It is given that density and Young’s modulus of the rod are r and Y respectively.
View SolutionA thin uniform copper rod of length l and mass m rotates uniformly with an angular velocity ω in a horizontal plane about a vertical axis passing through one of its ends. Determine the tension in the rod as a function of the distance r from the rotation axis. Find the elongation of the rod.
View SolutionA long uniform rod of length L, mass M is free to rotate in a horizontal plane about a vertical axis through its end. Two springs of constant K each are connected as shown. On equilibrium, the rod was horizontal. The frequency will be –
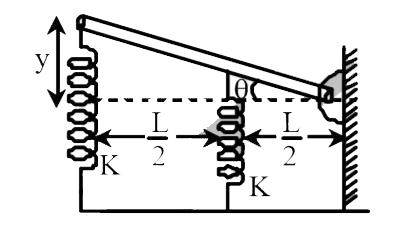
View SolutionA uniform rod of length l, mass m, cross-sectional area A and Young's modulus Y is rotated in horizontal plane about a fixed vertical axis passing through one end, with a constant angular velocity ω. Find the total extension in the rod due to the tension produced in the rod.
View SolutionA uniform rod AB of length l rotating with an angular velocity ω while its centre moves with a linear velocity v=ωl6 If the end A of the rod is suddenly fixed, the angular velocity of
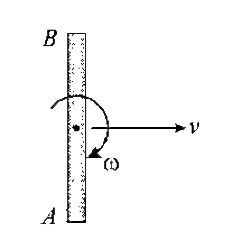
View Solution