A uniform rod of length 1m having mass 1kg rests against a smooth wall at an angle of 30∘ with the ground. Calculate the force exerted by the ground on the rod. Take g=10ms−2.
In Fig AB is a uniform rod of length 1m with centre at C,∠BAE=30∘,AC=0.5m
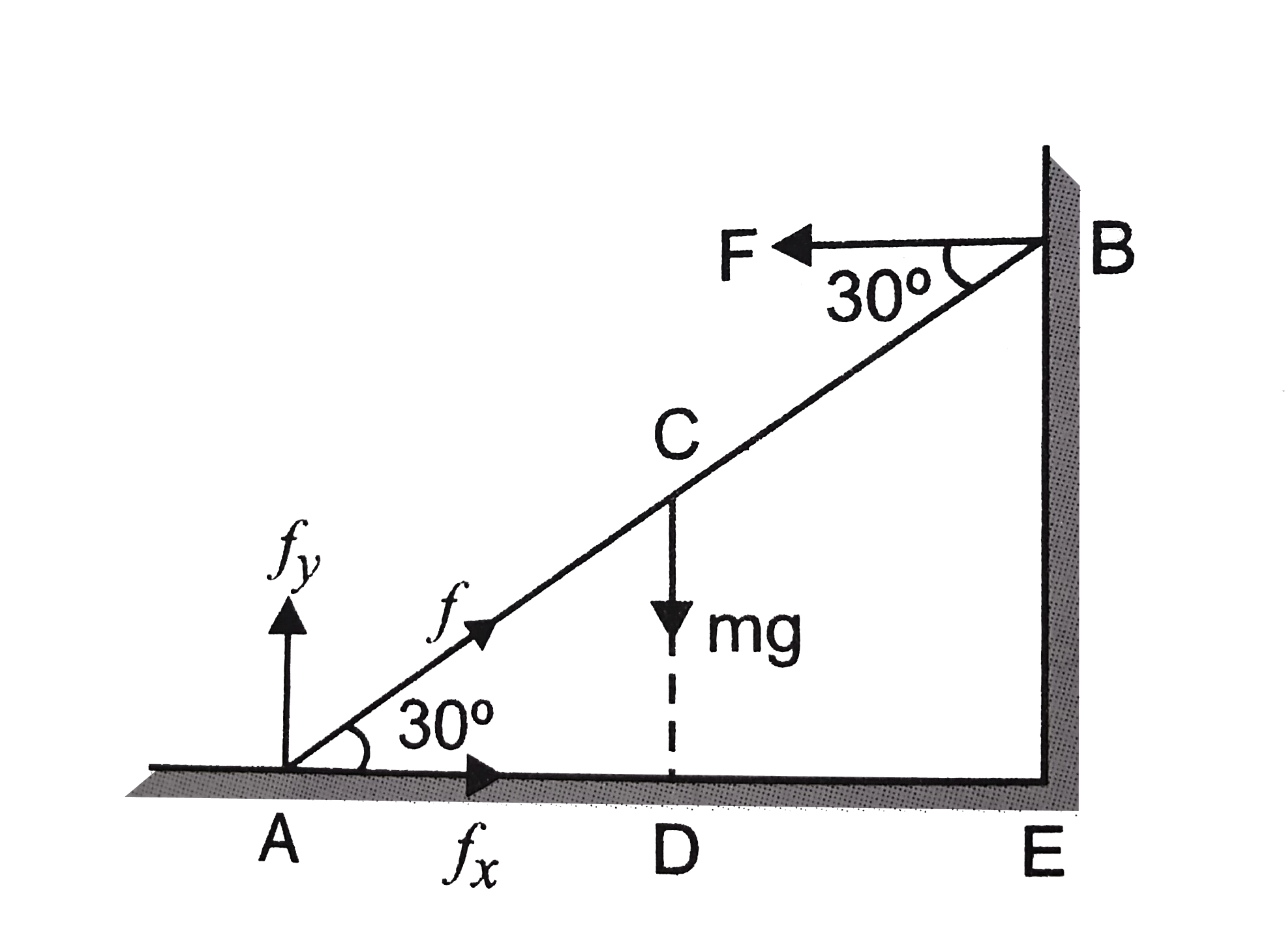
The various force involved are :
(i) Weight mg of the rod acting vertically downwards at C.
(ii) Horizontal force F due to the wall at B.
(iii) Reaction of floor f acting along AB. This is the force extered by the ground on the rod. It is the resultant of normal reaction fy of floor and force of friction fx along AE (that prevents slioding away of the rod from the wall).
In eqilibrium,
(i) net force on the rod along the ground is zero.
fx−F=0orfx=F ...(1)
(ii) net force on the rod perpendicular to the ground is zero.
fy−mg=0orfy=mg=1×10=10N
(iii) Algebraic sum of moments of force about A=0
F×BE=mg×AD
F×(ABsin30∘)=mg×ACcos30∘
F×1×12=1×10×0.5×√32
F=5√3=8.66N
From (1), fx=F=8.66N
Force exerted by the ground on the rod
f=√f2x+f2y=√8.662+102=13.22N
Topper's Solved these Questions
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBook:PRADEEPChapter:SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONExercise:PROBLEMS FOR PRACTICE TYPE B
Explore 2 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBook:PRADEEPChapter:SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONExercise:PROBLEMS FOR PRACTICE TYPE C
Explore 2 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBook:PRADEEPChapter:SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONExercise:PROBLEMS FOR PRACTICE TYPE A
Explore 2 Videos
- RAY OPTICSBook:PRADEEPChapter:RAY OPTICSExercise:Problem For Practice(a)
Explore 25 Videos
- THERMODYNAMICSBook:PRADEEPChapter:THERMODYNAMICSExercise:Assertion- Reason Type Questions
Explore 19 Videos
Similar Questions
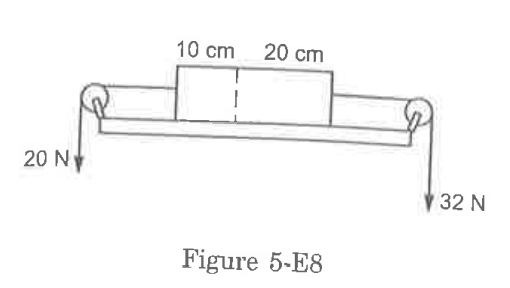
Figure shwos a uniform rod of length 30 cm having a mass of 3.0 kg. The strings shownin the figure are pulled by constant forces of 20 N and 32N. Find the force exerted by the 20 cm part of the rod on the 10 cm part. All the surfaces are smoth and the strings and the pulleys are light.
View SolutionA uniform rod of length L rests against a smooth roller as shown in figure. Find the friction coefficient between the ground and the lower end if the minimum angle that rod can make with the horizontal is θ.

View Solution
Knowledge Check
A uniform - ladder of length 70 m and weight W rests against a vertical wall at an angle of 45∘ with the wall. The coefficient of friction of the ladder with the ground and the wall are 12 and 13 respectively. A man of weight W/2 climbs the ladder without slipping. The height in metres to which he can climb is
A30B40C50D60A uniform thin rod of length 1m and mass 3 kg is attached to a uniform thin circular disc ois
A0.375 mB0.25mC0.125mD0.475mA 10kg ball attached at the end of a rigid massless rod of length 1m rotates at constant speed in a horizontal circle of radius 0.5m and period of 1.58s , as shown in the figure. The force exerted by the rod on the ball is (g=10ms−2)
 A158NB128NC110ND98N
A158NB128NC110ND98N
A uniform rod of length L rests against a smooth roller as shown in figure. Find the friction coefficient between the ground and the lower end if the minimum angle that rod can make with the horizontal is θ.

View SolutionFigure shows a uniform rod of length 30 cm having a mass 3.0 kg. The rod is pulled by constant forces of 20N and 32N as shown. Find the force exerted by 20 cm part of the rod on the 10 cm part (all surfaces are smooth) is

View SolutionA uniform ladder of mass 10 kg leans against a smooth vertical wall making an angle of 530 with it. The other end rests on a rough horizontal floor. Find the normal force and the frictional force that the floor exerts on the ladder
View SolutionA solid sphere of mass 2 kg and radius R rolls on a smooth horizontal surface at 5ms−1 and then rolls up on a smooth inclined plane of inclination angle 30∘ with horizontal. Calculate the height (in m ) attained by the sphere before it stops.(Take g=10ms−2)
View SolutionA uniform rod AB of length a hangs with one end against a smooth vertical wall, being supported by a string of length l, attached to the other end of the rod and to a point of the rod vertically above B. If the rod rests inclined to the wall at angle θ then cos2θ=
View Solution
