Question

A uniform rod of length $l$ and mass $2m$ rests on a smooth horizontal table. A point mass $m$ moving horizontally at right angles to the rod with initial velocity $v$ collides with one end of the rod and sticks to it.
Determine the position of the point on the rod which remains stationary immediately after collision.

Options

A. The point is a distance `(1//3) l` from the end where the mass strikes.
B. The point is a distance `(2//3) l` from the end where the mass strikes.
C. The point is a distance `(2//5) l` from the end where the mass strikes
D. The point is a distance` (1//5) l` from the end where the mass strikes

Answer

B

Explanation

Form the conservation of the linear momentum.
`mv=(m+2m)v_(CM)`
`implies v+(CM)=v/3`

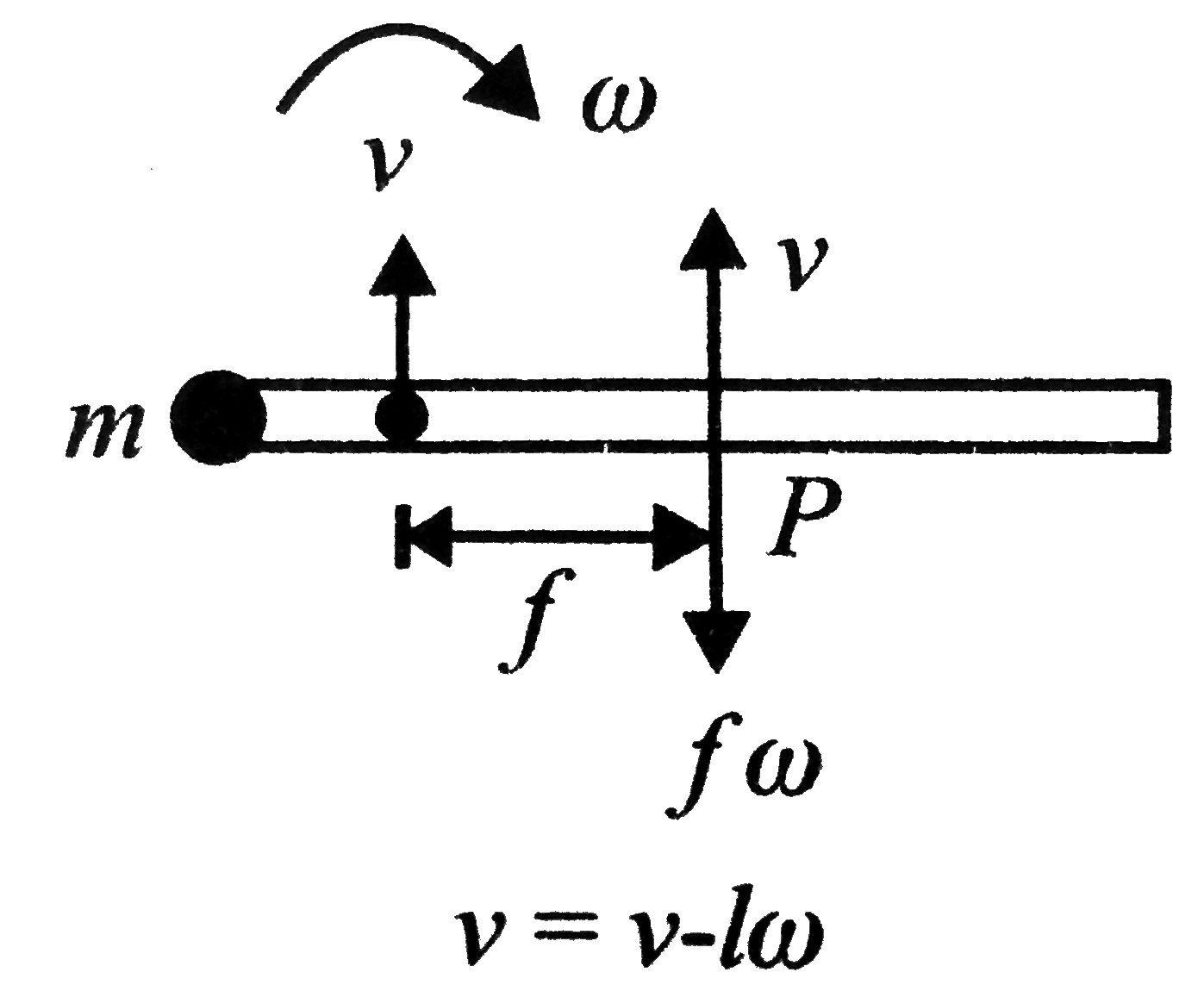
Let the point whose insantaneous velocity just after collisiion is zero be at a distance `I_(0)` from the centre of mass of the composite system.
`v_(CM)-l_(0)omega=0`
`implies v/3-l_(0)(v/l)=0impliesl_(0)=l/3`
The point is a distance `(2/3)l` from the end where the mass strikes.