A uniform rod of length l is pivoted distance x from the top of the rod . Neglecting friction find the (a) value of x for minimum period of oscillation, (b) minimum period of oscillation of the rod.

a. For minimum time period, we have
r=kandk=√lC/m
Substituting lC=ml2/12 for the rod, we have
r=12√3
Then, x=1/2−r.
where r=l/2√3
This gives x=121−(1)√3
b. Tmin=2π√2kg
where k=12√3
This gives
Tmin=2π√l√3g
Topper's Solved these Questions
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Subjective
21 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Single Correct
107 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Exercise 4.1
23 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Interger
11 Videos
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Interger type
3 Videos
Similar Questions
A uniform rod of length 1.00 m is suspended through an end and is set into oscillation with small amplitude under gravity. Find the time period of oscillation.
View SolutionThe end of the rod which is connected to the spring is pushed down and released. Find time period of oscillation of the rod ?
View Solution
Knowledge Check
In the compound pendulum, the minimum period of oscillation will be :
A2π√kgB2π√lgC2π√2lgD2π√2kgA thin uniform rod of length l is pivoted at its upper end. It is free to swing in a vertical plane. Its time period for oscillation of small amplitude is
A2π√lgB2π√2l3gC2π√3l2gD2π√l3gA unifrom rod of mass m and length l0 is pivoted at one end and is hanging in the vertical at one end and is hagingh in the vertical direction.The period of small angular oscillations of the rod is
 AT=3π√2l03gBT=4π√l03gCT=4π√2l03gDT=2π√2l03g
AT=3π√2l03gBT=4π√l03gCT=4π√2l03gDT=2π√2l03g
A uniform rod of mass m and length l is pivoted smoothly at O. A horizontal force acts at the bottom of the rod.
a. Find the angular velocity of the rod as the function of angle of rotation θ.
b.What is the maximum angular displacement of the rod?
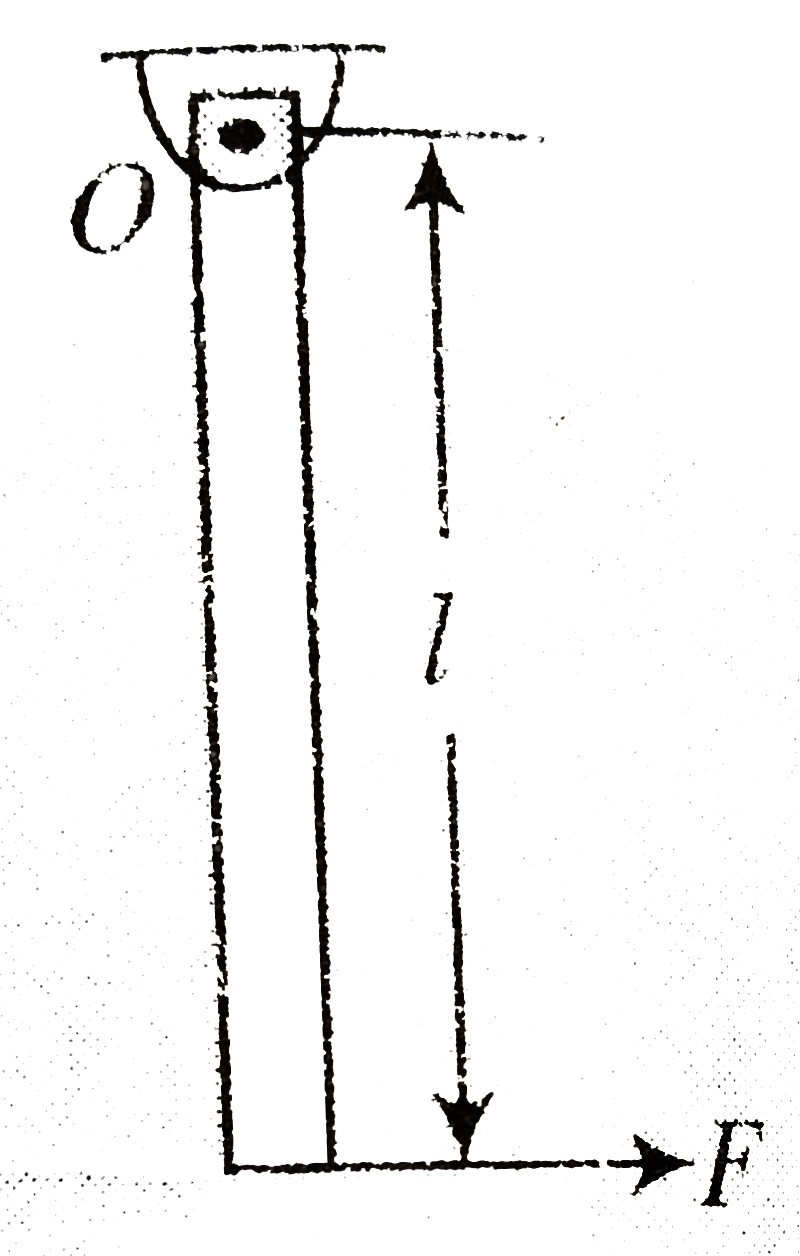
View SolutionA uniform rod ofmass M and length L is hanging from its one end free to rotate in a veritcal plane.A small ball of equal mass is attached of the lowe end as shown. Time period of small oscillations of the rod is
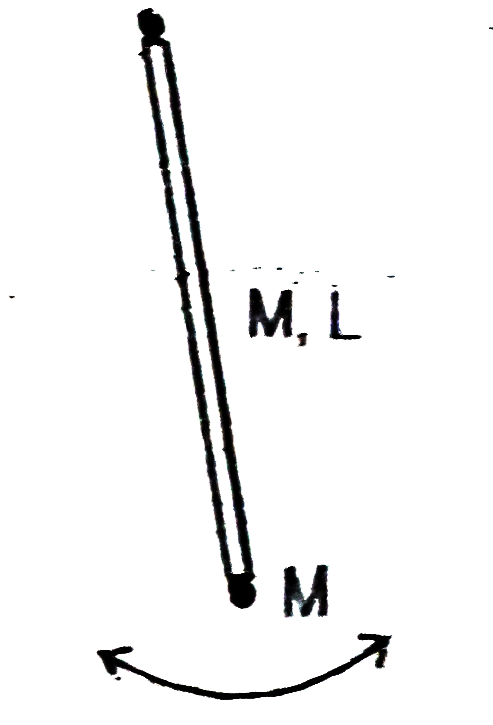
View SolutionA uniform straight rod of mass ' m (kg)&≤n>hLish∈≥dato≠end.Itisee→oscillate∈verticalpla≠.Ap∮mass(mkg)isaached→itatadistancexomtheh∈≥.Thevalueofxforwhichtimeperiodofoscillationswillbeminiμmis(L)/(n).F∈dn.((Use:) sqrt((7)/(3))=1.5)
View SolutionA uniform rod of length 2.0 m is suspended through an end and is set into oscillation with small amplitude under gravity. The time period of oscillation is approximately
View SolutionA uniform stick of length l is mounted so as to rotate about a horizontal axis perpendicular to the stick and at a distance d from the centre of mass. The time period of small oscillation has a minimum value when d/l is
View Solution
