A uniform rod of length l is suspended by end and is made to undego small oscillations. Find the length of the simple pendulum having the time period equal to that of the rod.
The correct Answer is:(2l)/3
To solve the problem of finding the length of a simple pendulum that has the same time period as a uniform rod of length L suspended at one end and undergoing small oscillations, we will follow these steps:
Step 1: Determine the Moment of Inertia of the Rod
The moment of inertia I of a uniform rod about an end is given by the formula:
I=13ML2
However, we will also use the parallel axis theorem to find the moment of inertia about the pivot point (end of the rod). The formula for the moment of inertia using the parallel axis theorem is:
I=Icm+Mh2
where:
- Icm=112ML2 (moment of inertia about the center of mass),
- h=L2 (distance from the center of mass to the pivot).
Substituting these values:
I=112ML2+M(L2)2
=112ML2+ML24
=112ML2+312ML2=412ML2=13ML2
Step 2: Calculate the Time Period of the Rod
The time period T for small oscillations of the rod is given by:
T=2π√IMgh
Substituting I=13ML2 and h=L2:
T=2π
⎷13ML2MgL2
=2π
⎷L23g⋅L2
=2π√2L3g
Step 3: Find the Length of the Simple Pendulum
The time period of a simple pendulum is given by:
T=2π√Lpg
where Lp is the length of the simple pendulum. Setting the two expressions for T equal:
2π√2L3g=2π√Lpg
Canceling 2π and squaring both sides:
2L3g=Lpg
Multiplying both sides by g:
2L3=Lp
Final Result
Thus, the length of the simple pendulum that has the same time period as the rod is:
Lp=2L3
The moment of inertia I of a uniform rod about an end is given by the formula:
I=13ML2
However, we will also use the parallel axis theorem to find the moment of inertia about the pivot point (end of the rod). The formula for the moment of inertia using the parallel axis theorem is:
I=Icm+Mh2
where:
- Icm=112ML2 (moment of inertia about the center of mass),
- h=L2 (distance from the center of mass to the pivot).
I=112ML2+M(L2)2
=112ML2+ML24
=112ML2+312ML2=412ML2=13ML2
The time period T for small oscillations of the rod is given by:
T=2π√IMgh
Substituting I=13ML2 and h=L2:
T=2π
⎷13ML2MgL2
=2π
⎷L23g⋅L2
=2π√2L3g
The time period of a simple pendulum is given by:
T=2π√Lpg
where Lp is the length of the simple pendulum. Setting the two expressions for T equal:
2π√2L3g=2π√Lpg
Canceling 2π and squaring both sides:
2L3g=Lpg
Multiplying both sides by g:
2L3=Lp
Thus, the length of the simple pendulum that has the same time period as the rod is:
Lp=2L3
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - HC VERMACHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Objective-2
2 Videos
- ROTATIONAL MECHANICSBOOK - HC VERMACHAPTER - ROTATIONAL MECHANICSEXERCISE - Exercises
86 Videos
- SOME MECHANICAL PROPERTIES OF MATTERBOOK - HC VERMACHAPTER - SOME MECHANICAL PROPERTIES OF MATTEREXERCISE - Exercises
32 Videos
Similar Questions
A uniform rod of length l is suspended from a point P. and the rod is made to undergo small oxcillations. Match the following
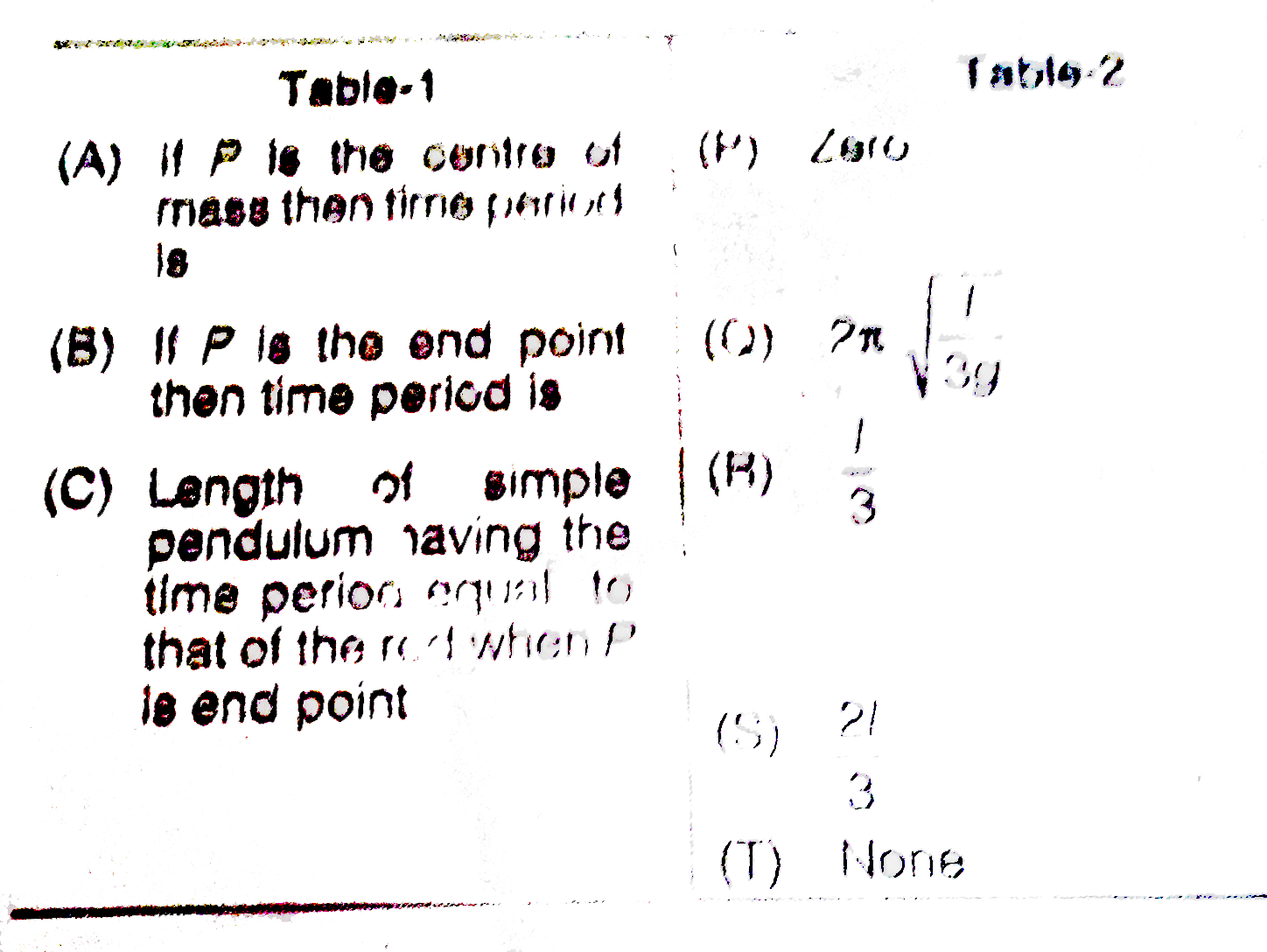
View SolutionA uniform rod of length 1.00 m is suspended through an end and is set into oscillation with small amplitude under gravity. Find the time period of oscillation.
View Solution
Knowledge Check
A uniform rod of mass m and length l is suspended about its end. Time period of small angular oscillations is
 A2π√lgB2π√2lgC2π√2l3gD2π√l3g
A2π√lgB2π√2lgC2π√2l3gD2π√l3gA uniform rod of length 2.0 m is suspended through an end and is set into oscillation with small amplitude under gravity. The time period of oscillation is approximately
A1.60secB1.80 secC2.0 secD2.40 secIf the length of a simple pendulum is equal to the radius of the earth, its time period will be
A2π√R/gB2π√R/2gC2π√2R/gDinfinite
A uniform rod of length 2.0 m is suspended through its endpoint about which it performs small angular oscillations in the vertical plane, its time period is nearly
View SolutionA uniform rod of length l oscillates about an axis passing through its end. Find the oscillation period and the reduced length of this pendulum.
View SolutionWhat is the time period of a simple pendulum if length of the pendulum is equal to the radius of Earth ?
View SolutionTwo iron rods of length of 2.2 m and 0.8 m of uniform densities are suspended from their ends and made of oscillate. Find the time periods of the two rods. Which rod gains time as compared to the time period of seconds pendulum ?
View SolutionIn a simple pendulum the period of oscillation (T) is related to the length of the pendulum (L) as
View Solution
