A uniform rod of length l, mass m, cross-sectional area A and Young's modulus Y is rotated in horizontal plane about a fixed vertical axis passing through one end, with a constant angular velocity ω. Find the total extension in the rod due to the tension produced in the rod.
2mω2l23AY
mω2l2AY
mω2l23AY
5mω2l248AY
The correct Answer is:C
To solve the problem of finding the total extension in a uniform rod of length l, mass m, cross-sectional area A, and Young's modulus Y when it is rotated about a fixed vertical axis with a constant angular velocity ω, we can follow these steps:
1. Identify the Mass Element:
- Consider a small element of the rod at a distance x from the axis of rotation with a length dx.
- The mass of this small element can be expressed as:
\(
dm = \frac{m}{l} \cdot dx = \mu \cdot dx
\)
where \(\mu = \frac{m}{l}\) is the mass per unit length.
2. Calculate the Centripetal Force:
- The centripetal force acting on this mass element due to its rotation is given by:
\(
dT = dm \cdot \omega^2 \cdot x = \mu \cdot \omega^2 \cdot x \cdot dx
\)
3. Relate Tension to the Extension:
- The tension at a distance x from the axis of rotation is the sum of the contributions from all elements of the rod from x to l. Thus, we can write:
\(
T(x) = \int_x^l dT = \int_x^l \mu \cdot \omega^2 \cdot x \cdot dx
\)
- Evaluating this integral gives:
\(
T(x) = \mu \cdot \omega^2 \int_x^l x \cdot dx = \mu \cdot \omega^2 \left( \frac{x^2}{2} \right)_x^l = \mu \cdot \omega^2 \left( \frac{l^2}{2} - \frac{x^2}{2} \right)
\)
4. Calculate the Extension of Each Element:
- The extension \(dL\) of the small element \(dx\) can be expressed using Young's modulus:
\(
Y = \frac{T}{A} \cdot \frac{dL}{dx} \implies dL = \frac{T \cdot dx}{Y \cdot A}
\)
- Substituting for \(T\):
\(
dL = \frac{\mu \cdot \omega^2 \left( \frac{l^2}{2} - \frac{x^2}{2} \right) \cdot dx}{Y \cdot A}
\)
5. Integrate to Find Total Extension:
- The total extension \(L\) of the rod is obtained by integrating \(dL\) from \(0\) to \(l\):
\(
L = \int_0^l dL = \int_0^l \frac{\mu \cdot \omega^2 \left( \frac{l^2}{2} - \frac{x^2}{2} \right)}{Y \cdot A} \cdot dx
\)
- Evaluating this integral gives:
\(
L = \frac{\mu \cdot \omega^2}{2Y \cdot A} \left( l^2x - \frac{x^3}{3} \right)_0^l = \frac{\mu \cdot \omega^2}{2Y \cdot A} \left( l^3 - \frac{l^3}{3} \right) = \frac{\mu \cdot \omega^2 l^3}{3Y \cdot A}
\)
6. Substitute for \(\mu\):
- Recall that \(\mu = \frac{m}{l}\):
\(
L = \frac{m \cdot \omega^2 l^2}{3Y \cdot A}
\)
Final Result:
The total extension in the rod due to the tension produced is:
\(
L = \frac{m \cdot \omega^2 \cdot l^2}{3Y \cdot A}
\)
- Consider a small element of the rod at a distance x from the axis of rotation with a length dx.
- The mass of this small element can be expressed as:
\(
dm = \frac{m}{l} \cdot dx = \mu \cdot dx
\)
where \(\mu = \frac{m}{l}\) is the mass per unit length.
- The centripetal force acting on this mass element due to its rotation is given by:
\(
dT = dm \cdot \omega^2 \cdot x = \mu \cdot \omega^2 \cdot x \cdot dx
\)
- The tension at a distance x from the axis of rotation is the sum of the contributions from all elements of the rod from x to l. Thus, we can write:
\(
T(x) = \int_x^l dT = \int_x^l \mu \cdot \omega^2 \cdot x \cdot dx
\)
- Evaluating this integral gives:
\(
T(x) = \mu \cdot \omega^2 \int_x^l x \cdot dx = \mu \cdot \omega^2 \left( \frac{x^2}{2} \right)_x^l = \mu \cdot \omega^2 \left( \frac{l^2}{2} - \frac{x^2}{2} \right)
\)
- The extension \(dL\) of the small element \(dx\) can be expressed using Young's modulus:
\(
Y = \frac{T}{A} \cdot \frac{dL}{dx} \implies dL = \frac{T \cdot dx}{Y \cdot A}
\)
- Substituting for \(T\):
\(
dL = \frac{\mu \cdot \omega^2 \left( \frac{l^2}{2} - \frac{x^2}{2} \right) \cdot dx}{Y \cdot A}
\)
- The total extension \(L\) of the rod is obtained by integrating \(dL\) from \(0\) to \(l\):
\(
L = \int_0^l dL = \int_0^l \frac{\mu \cdot \omega^2 \left( \frac{l^2}{2} - \frac{x^2}{2} \right)}{Y \cdot A} \cdot dx
\)
- Evaluating this integral gives:
\(
L = \frac{\mu \cdot \omega^2}{2Y \cdot A} \left( l^2x - \frac{x^3}{3} \right)_0^l = \frac{\mu \cdot \omega^2}{2Y \cdot A} \left( l^3 - \frac{l^3}{3} \right) = \frac{\mu \cdot \omega^2 l^3}{3Y \cdot A}
\)
- Recall that \(\mu = \frac{m}{l}\):
\(
L = \frac{m \cdot \omega^2 l^2}{3Y \cdot A}
\)
The total extension in the rod due to the tension produced is:
\(
L = \frac{m \cdot \omega^2 \cdot l^2}{3Y \cdot A}
\)
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - Matrix Matching12videos
PROPERTIES OF MATTER
- BOOK - DC PANDEY ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - Integer8videos
PROPERTIES OF MATTER
- BOOK - DC PANDEY ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - More than one option is correct21videos
PROPERTIES OF MATTER
- BOOK - DC PANDEY ENGLISHCHAPTER - PROJECTILE MOTIONEXERCISE - Level - 2 Subjective10videos
PROJECTILE MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Integer type q.14videos
RAY OPTICS
Similar Questions
A stell rod of length 2l corss sectional area A and mass M is set rotating in a horizotnal plane about an axis passing through its cnetre and perpendicular to its length with constant angular velcoty ω. If Y is the Young's modulus for steel, find the extension in the lenght of the rod. (Assume the rod is uniform.)
View SolutionA rod is rotating with angular velocity ω about axis AB. Find cosθ.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A uniform rod of mass m. length L, area of cross- secticn A is rotated about an axis passing through one of its ends and perpendicular to its length with constant angular velocity omega in a horizontal plane If Y is the Young's modulus of the material of rod, the increase in its length due to rotation of rod is
Amω2L2AYBmω2L22AYCmω2L23AYD2mω2L2AY
A uniform cylindrical rod of length L, cross-section area A and Young's modulus Y is acted upon by the force as shown in Fig. 7(CF).3. The elongation of the rod is
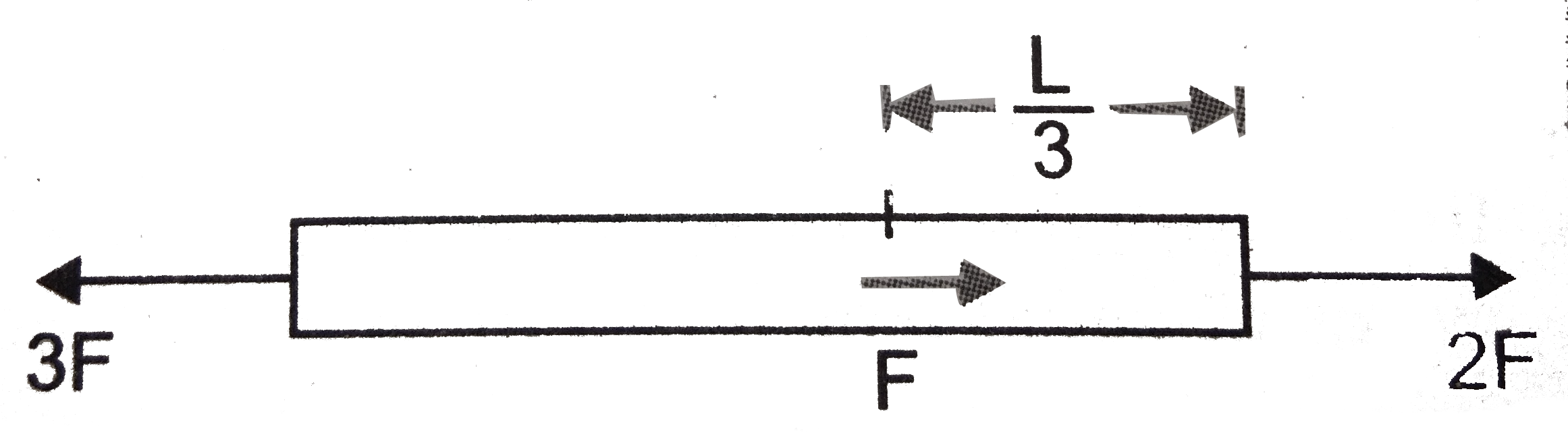 View Solution
View SolutionA thin uniform copper rod of length l and mass m rotates uniformly with an angular velocity ω in a horizontal plane about a vertical axis passing through one of its ends. Determine the tension in the rod as a function of the distance r from the rotation axis. Find the elongation of the rod.
View SolutionA uniform rod of mass m and length l rotates in a horizontal plane with an angular velocity ω about a vertical axis passing through one end. The tension in the rod at a distance x from the axis is
View SolutionA uniform rod AB of length 2l and mass m is rotating in a horizontal plane about a vertical axis through A, with angular velocity ω, when the mid-point of the rod strikes a fixed nail and is brought immediately to rest. Find the impulse exerted by the nail.
View SolutionA rod of mass M and length l attached with a small bob of mass m at its end is freely rotating about a vertical axis passing through its other end with a constant angular speed ω. Find the force exerted by the system (rod and bob) on the pivot. Assume that gravity is absent.
View Solution
A uniform rod of length L is free to rotate in a vertical plane about a fixed horizontal axis through B. The rod begins rotating from rest. The angular velocity ω at angle θ is given asView Solution
A uniform rod of legth L is free to rotate in a vertica plane about a fixed horizontal axis through B. The rod begins rotating from rest. The angular velocity ω at angle θ is given asView Solution

