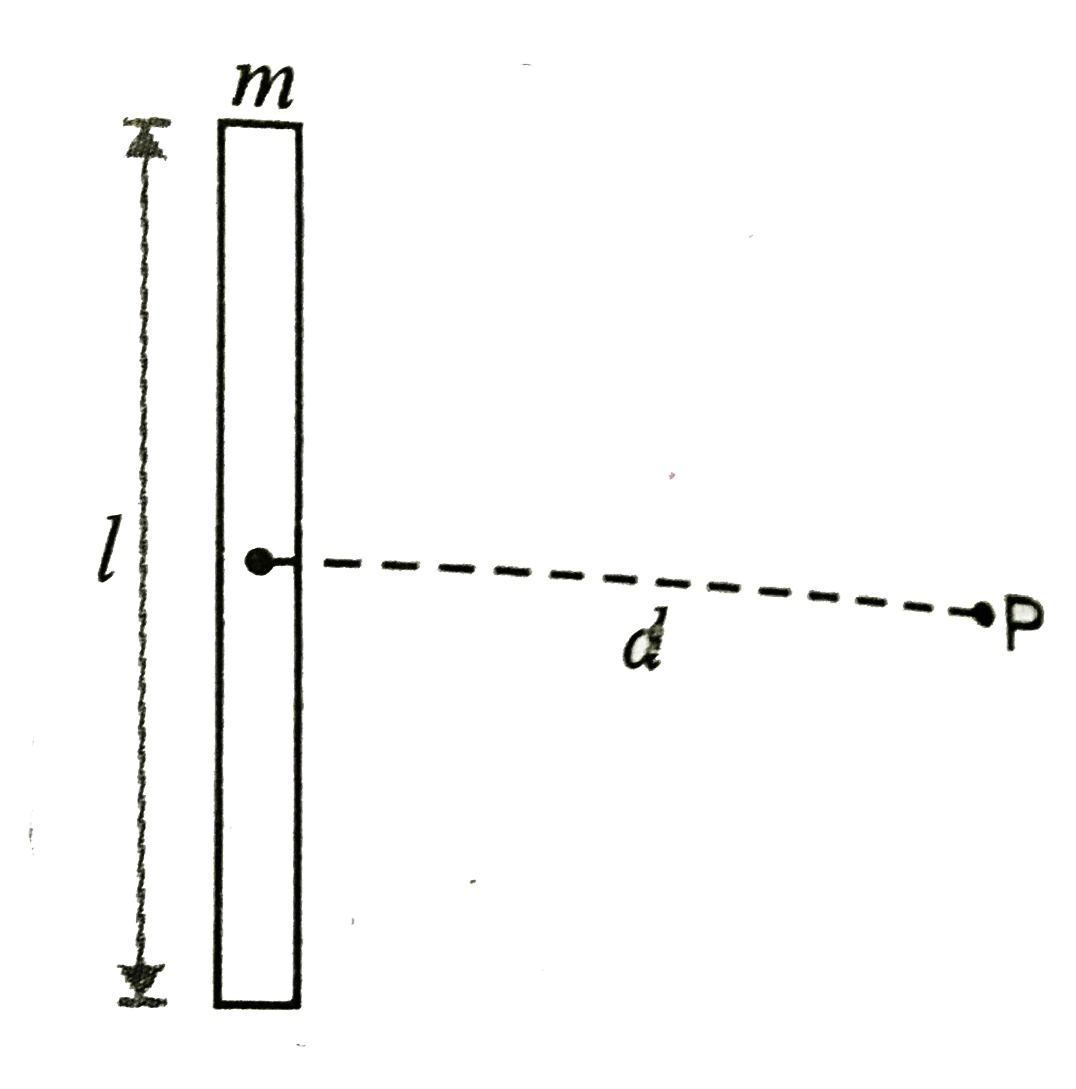
A uniform rod of mass $m$ and length $l$ is taken. Find the gravitational field intensity at point $P$ at distance $d$ which is on the perpendicular bisector of the rod as shown in Fig.

A

$\frac{4 G m}{d \sqrt{4 d^{2} + l^{2}}}$

B

$\frac{2 G m}{d \sqrt{l^{2} + 4 d^{2}}}$

C

$\frac{2 \sqrt{2} G m}{d \sqrt{l^{2} + 4 d^{2}}}$

D

none of the above

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

Consider element of the rod of width $x$ as shown in Fig.

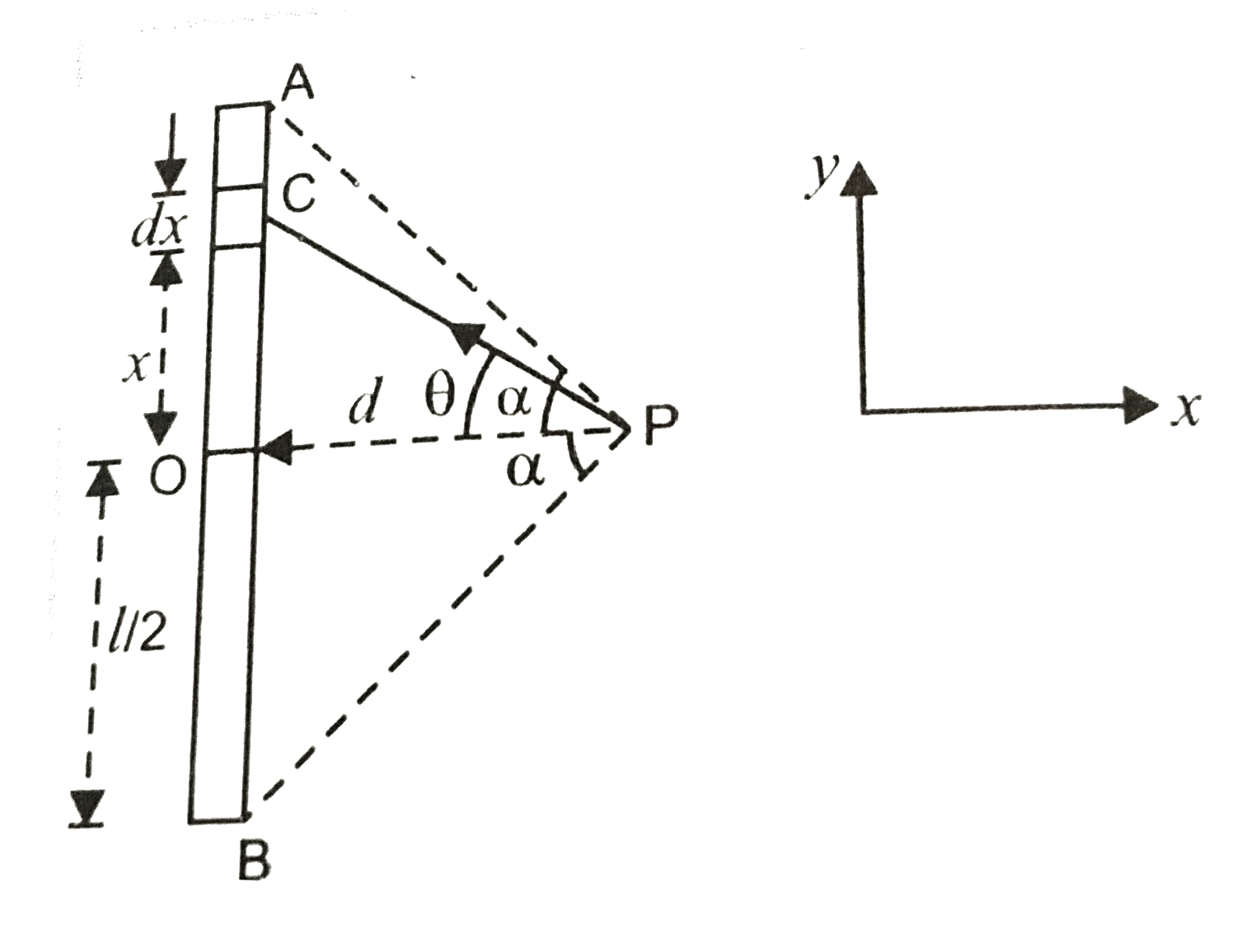
Mass of element, $d m = \frac{m}{l} d x$
Gravitaitonal field intensity at $P$ due to this element is
$d I = \frac{G d m}{x^{2} + d^{2}} = \frac{G}{(x^{2} + d^{2})} \times \frac{m}{l} d x$ along $P C$
In $δ O P C, x = d tan θ$ and $d x = d {sec}^{2} θ d θ$
$∴ x^{2} + d^{2} = d^{2} ({tan}^{2} θ + 1) = d^{2} {sec}^{2} θ$
$∴ d I = \frac{G m}{l} \frac{d {sec}^{2} θ d θ}{d^{2} {sec}^{2} θ} = \frac{G m}{l d} d θ$
resolving $d \to I$ into two rectangular components we have $d I cos θ$ acts along $P O$ and $d I sin θ$ acts perpendicular to $P O$ .
If we find the gravitaitonal field due to other elements of the rod at $P$ and resolve them into two rectangular componets, we note that the components of gravitational field intensity perpendicular to $O P$ will cancel out and components of gravitational intensity along $P O$ will be added up. Therefore, total gravitational intensity at $P$ due to entire rod is
$I = \int_{- α}^{+ α} d I cos θ = \int_{- α}^{+ α} \frac{G m}{l d} cos θ d θ$
$= \frac{G m}{l d} [2 sin α] = \frac{2 G m}{l d} \times \frac{l / 2}{\sqrt{{(l / 2)}^{2} + d^{2}}}$
$= \frac{2 G m}{d \sqrt{l^{2} + 4 d^{2}}}$

|

Updated on:21/07/2023

Class 11 PHYSICS GRAVITATION

Similar Questions

Knowledge Check

Question 1 - Select One
A thin uniform rod of mass M and length L. Find the radius of gyration for rotation about an axis passing through a point at a distance of $\frac{L}{4}$ from centre and perpendicular to rod.
A $\sqrt{\frac{7}{48} L}$
B $\sqrt{\frac{5}{48} L}$
C $\sqrt{\frac{7}{24} L}$
D $\sqrt{\frac{19}{24} L}$
Question 2 - Select One
A uniform rod $A B$ of mass $m$ and length $l$ is at rest on a smooth horizontal surface. An impulse $J$ is applied to the end $B$ , perpendicular to the rod in the horizontal direction. Speed of particlem $P$ at a distance $\frac{l}{6}$ from the centre towards $A$ of the rod after time $t = \frac{π m l}{12 J}$ is.
A $2 \frac{J}{m}$
B $\frac{J}{\sqrt{2} m}$
C $\frac{J}{m}$
D $\sqrt{2} \frac{J}{m}$
Question 3 - Select One or More
A uniform rod of mass M and length L carrying a charge q uniformly distributed over its length is rotated with constant velocity w about its mid point perpendicular to the rod. Its magnetic moment is
A $q ω L^{2} / 6$
B $q ω L^{2} / 12$
C $q ω L^{2} / 24$
D $q ω L^{2} / 48$

Recommended Questions

Home
Ask Doubt
Profile