A uniform rod of mass m, length l is placed over a smooth horizontal surface along y -axis and is at rest as shown in figure. An impulsive force F is applied for a small time along x-direction at point A. The x-coordinte of end A of the rod when the rod becomes parallel to x-axis for the first is (in itially the coordinates opf centre of mass of the rod is (0,0).

The correct Answer is:D
As torque change in momentum
(linear momentum)………i
and (angular momentum)..ii
Dividing eqn i and ii we get
using
Displacement of is
and
Dividing we get
coordinates of A will be
Topper's Solved these Questions
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Multiple Correct
26 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Linked Comprehension
71 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Subjective
19 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer
11 Videos
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer
16 Videos
Similar Questions
A uniform rod of mass m and length l is lying on a smooth table. An impulse J acts on the rod momentarily as shown in figure at point R. Just after that:


View SolutionA rod of length 2l is bent as shown in figure. Coordinates of centre of mass are
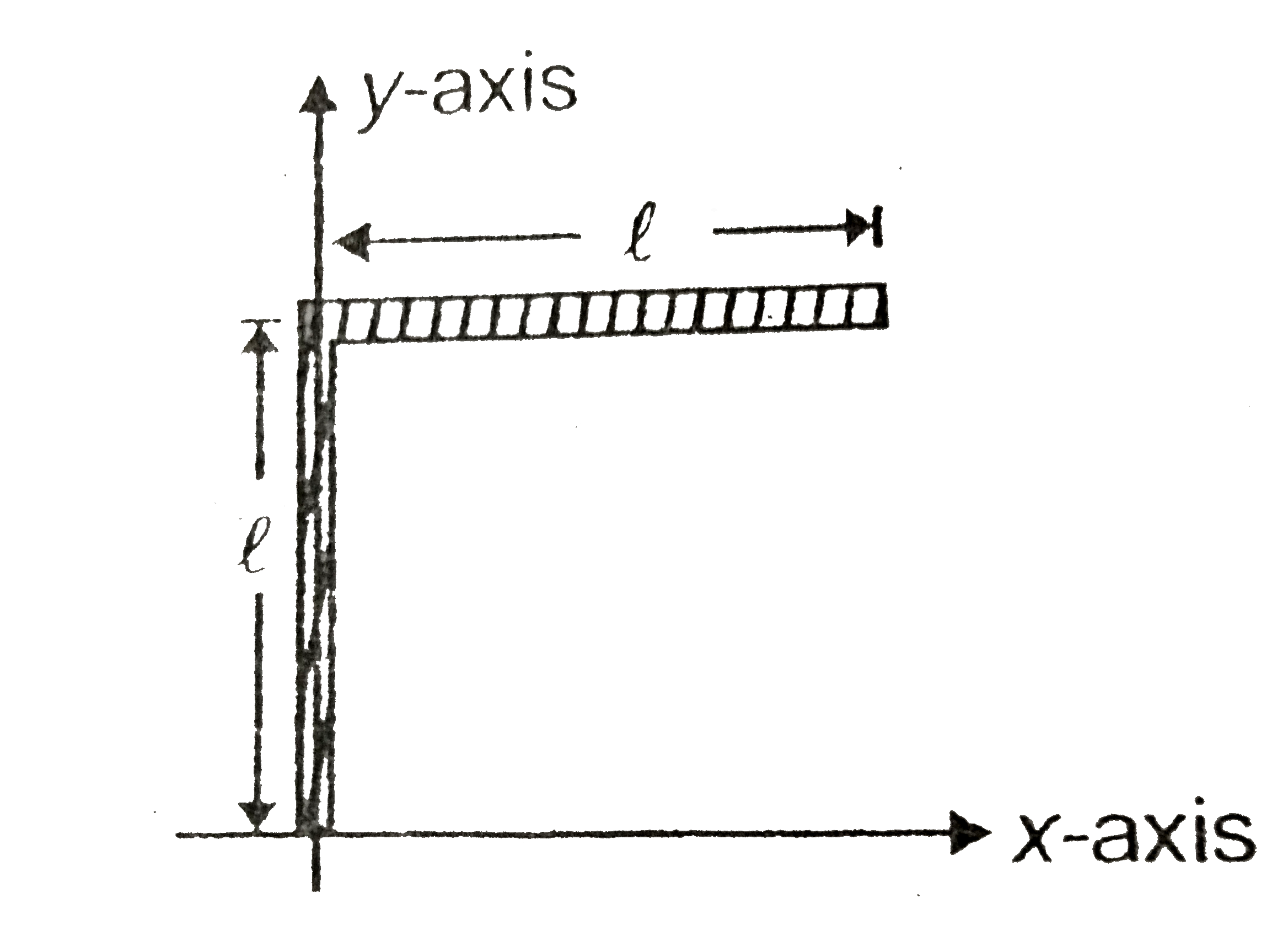
View SolutionA uniform rod of mass m length l is attached to smooth hinge at end A and to a string at end B as shown in figure. It is at rest. The angular acceleration of the rod just after the string is cut is :

View SolutionA uniform rod of mass m, length l rests on a smooth horizontal surface. Rod is given a sharp horizontal impulse p perpendicular to the rod at a distance l/4 from the centre. The angular velocity of the rod will be
View SolutionA uniform rod AB of mass m and length l at rest on a smooth horizontal surface . An impulse P is applied to the end B. The time taken by the rod to turn through a right angle is :

View SolutionA uniform rod AB of mass m and length l at rest on a smooth horizontal surface . An impulse P is applied to the end B. The time taken by the rod to turn through a right angle is :

View SolutionA uniform rod of mass M and length L, area of cross section A is placed on a smooth horizontal surface. Forces acting on the rod are shown in the digram

Total elastic potential energy stored in the rod is :
View SolutionA uniform straight rod is placed in vertical position on a smooth horizontal surface and released. As the rod is in motion, the centre of mass moves
View SolutionA rod of mass m and length l is hinged at one of its end A as shown in figure. A force F is applied at a distance x from A. The acceleration of centre of mass a varies with x as

View SolutionA rod of mass m and length l is hinged at one of its ends A as shown in figure. A force F is applied at a distance x from A . The acceleration of centre of mass varies with x as −
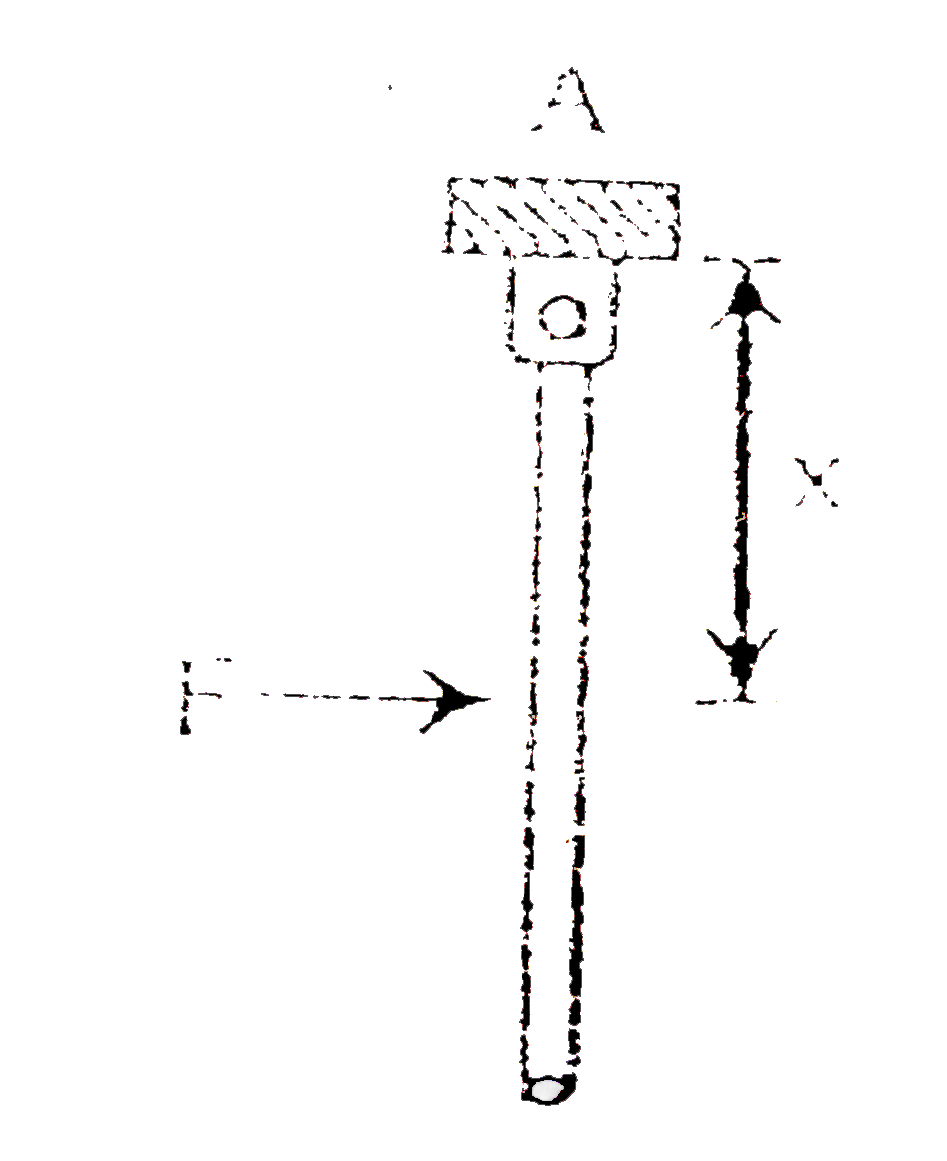
View Solution
