A uniform rod of mass m=1.5kg suspended by two identical threads l=90cm in length ( figure ) was turned through a small angle about the vertical axis passing through its middle point C. The threads deviated in the process through an angle α=5.0∘. Then the rod was released to start performing small oscillations.
Find:
(a) the oscillation period,
(b) the rod's oscillation energy.

(a) Let us locate the sytem when the threads are deviated through an angle α′<α, during the oscillations of the system ( figure). From the conservation of mechannical energy of the system :
12mL212θ2+mgl(1−cosα′)= constante (1)
where L is the length of the rod, θ is the angular deviation of the rod from its equilibrium position i.e.
θ=0
Differentiating Eqn. (1) w.r.t. time
12mL2122.θ..θ=mglsinα′.α′=0
So, L212.θ..θ+glα′.α′=0 ( for small α′,siniα′=α′)....(2)
But from the Figure,
L2θ=lα′ or a′=L2lθ
So,.α′=L3l.θ
Putting these values of α′ and dα′dt in Eqn. (2) we get
d2θdt2=−3glθ
Thus the sought time period
T=2πω0=2π√l3g
(b) The sought oscillation energy
E=Uextreme=mgl(1−cosα)=mgl2sin2(α2)
=mgl2α24=mglα22 ( because for small angle sinθ≅θ)

Topper's Solved these Questions
- OSCILLATIONS AND WAVESBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Electric Oscillations
56 Videos
- OSCILLATIONS AND WAVESBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Elastic Waves
39 Videos
- OPTICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OPTICSEXERCISE - Exercise
2 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Relativistic Mechanics
49 Videos
Similar Questions
A uniform rod of length l oscillates about an axis passing through its end. Find the oscillation period and the reduced length of this pendulum.
View SolutionThe moment of inertia of a thin uniform rod of mass M, length L, about an axis passing through its centre and making an angle θ with the rod is
View Solution
Knowledge Check
A horizontally orientied unifrom copper rod of length l is rotating about a vertical axis passing through its centre. Calculate the rotated frequency at which the rod ruptures. Breaking or rupture strength of copper is σ and density of copper is ρ.
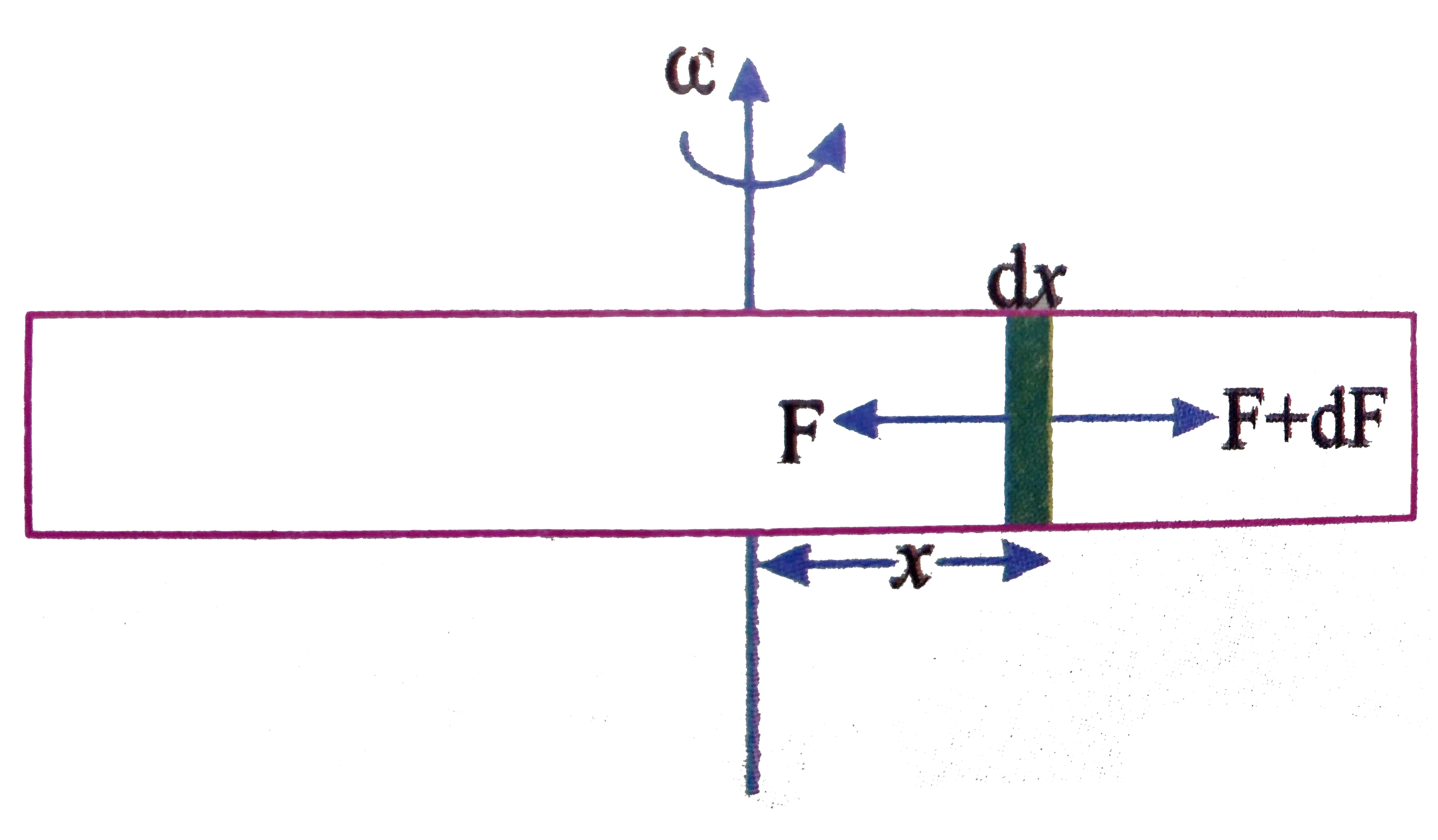 A1πl√2σmpBπl√2σmpC2πl√2σmpD3πl√2σmp
A1πl√2σmpBπl√2σmpC2πl√2σmpD3πl√2σmpA uniform rod of mass m and length l rotates in a horizontal plane with an angular velocity ω about a vertical axis passing through one end. The tension in the rod at a distance x from the axis is
A12mω2xB12mω2(1−x2l)C12mω2l(1−x2l2)D12mω2l[1−xl]A thin uniform rod of mass m and length L rotates with the constant angular velocity ω about .the vertical axis passing through the rod's suspensjon point O. It describes a carried surface, then:
Acentrifugal force acting on rod is mL2sinθω2 and will pass through centre of massBcentrifugal force acting on rod is mL2sinθω2 and will not pass through centre of massCθ=cos−1(3g2ω2L)Dθ=cos−1(gω2L)
Two identical rods each of mass M and length L are kept according to figure. Find the moment of inertia of rods about an axis passing through O and perpendicular to the plane of rods.

View Solutionfind the radius of gyration of a rod of mass m and length 2l about an axis passing through one of its eneds and perpendicular to its length.
View SolutionThe M.I. of thin uniform rod of mass 'M' and length 'l' about an axis passing through its centre and perpendicular to its length is
View SolutionTwo bodies of mass 1 kg and 2 kg are attached to the ends of a 2 metre long weight less rod . This system is rotating about an axis passing through middle point of rod . Calculate M. I of system .
View SolutionA uniform rod of mass m and length l is suspended about its end. Time period of small angular oscillations is

View Solution
