A uniform slender bar AB of mass m is suspended as shown from a small cart of the same mass m. Neglecting the effect of the friction, determine the accelerations of points A and B immediately after a horizontal force F has been applied at B.

Let the acceleration of bar and cart be a and a', respectively: also α be the angular acceleration of the bar.
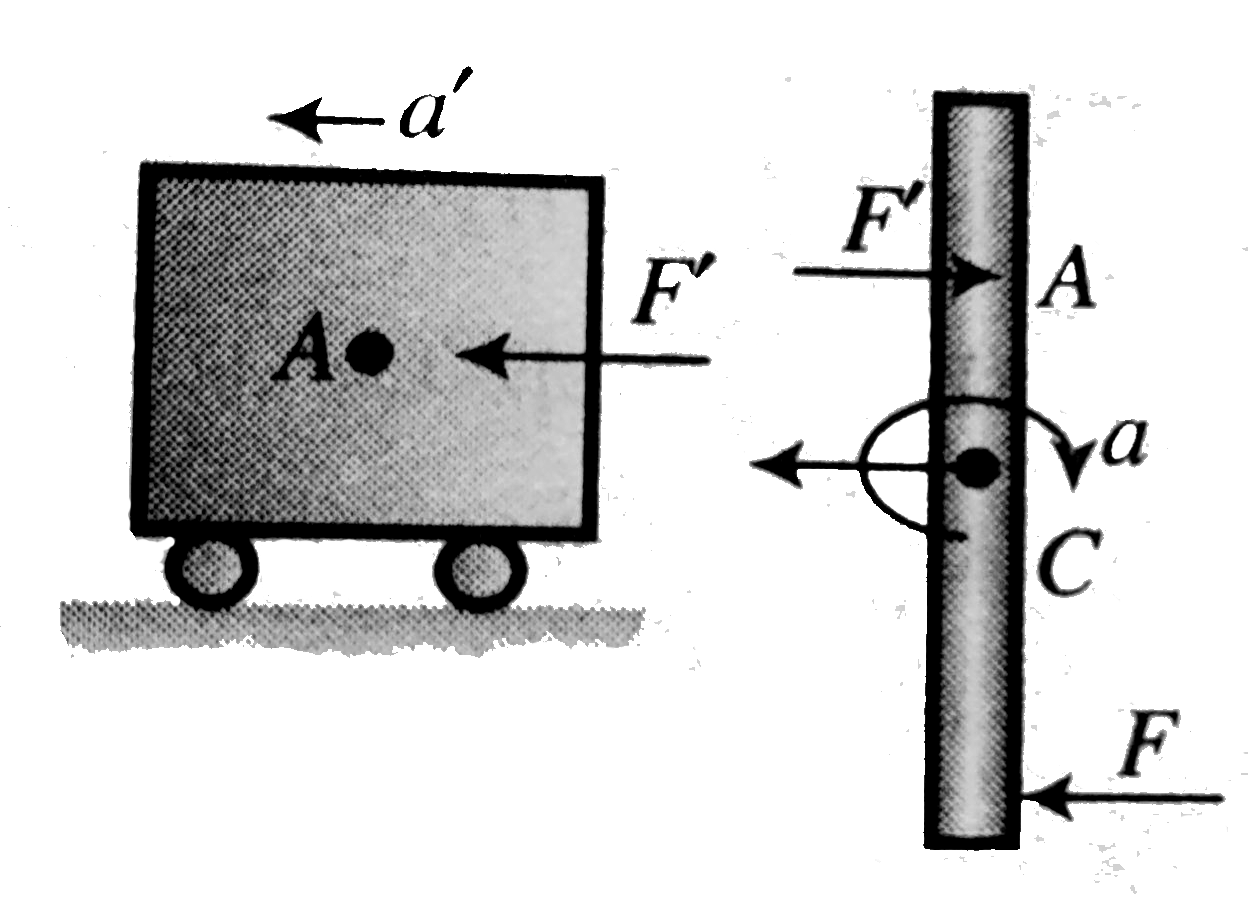
Writing newton's equation of motion
For the bar: F−F'=ma……i
For the cart F'=ma'..........ii
Torque equation for rod about centre of mass
For the rotation of the rod (F+F')L2=ML2α
F+F'=MLα6..........iii
The acceleration of point A on the rod will be same as the acceleration of the cart
→aA=→aA,C=→aC
−a'=αL2−a or a=a−L2α......iv
on solving eqn i, ii, iii, and iv we get
a=7F5m and α18F5mL
|a'|=|aA|=a−L2α=2F5m
|aB|=a+L2α=16F5m
Topper's Solved these Questions
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Exercise 2.1
6 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Exercise 2.2
17 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer
11 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICSCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE
2 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Interger
2 Videos
Similar Questions
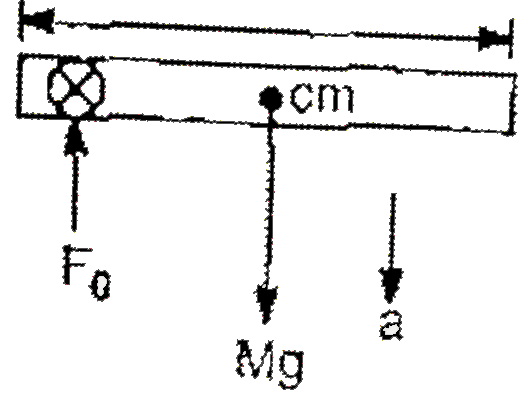
A uniform slender rod of length L and mass M is pivoted at one end. It is held horizontal and releasaed. Assume the pivot is frictionless. Find .
(a) the angular acceleration of the rod immediately after it is released, and
(b) the force F0 exerted on the rod by the pivot immediately after release.
View SolutionA uniform plate of mass m is suspended in each of the ways shown. For each case determine immediately after the connection at Bhas been released ,
(a) the angular acceleration of the plate.

(b) the acceleration of its mass center.
View Solution
Knowledge Check
If F is the force applied , then acceleration of the body of mass M when body is on rough horizontal surface
AfkMBF−fkMCFMDNone of theseA small bob mass 'm' is suspended by a massless string from a cart of the same mass 'm' as shown in the figure. The friction between the cart and horizontal ground is negligible. The bob is given a velocity V0 in horizontal direction as shown. The maximum height attained by the bob is , ( initially whole system ( bob + string + cart ) was at rest ).
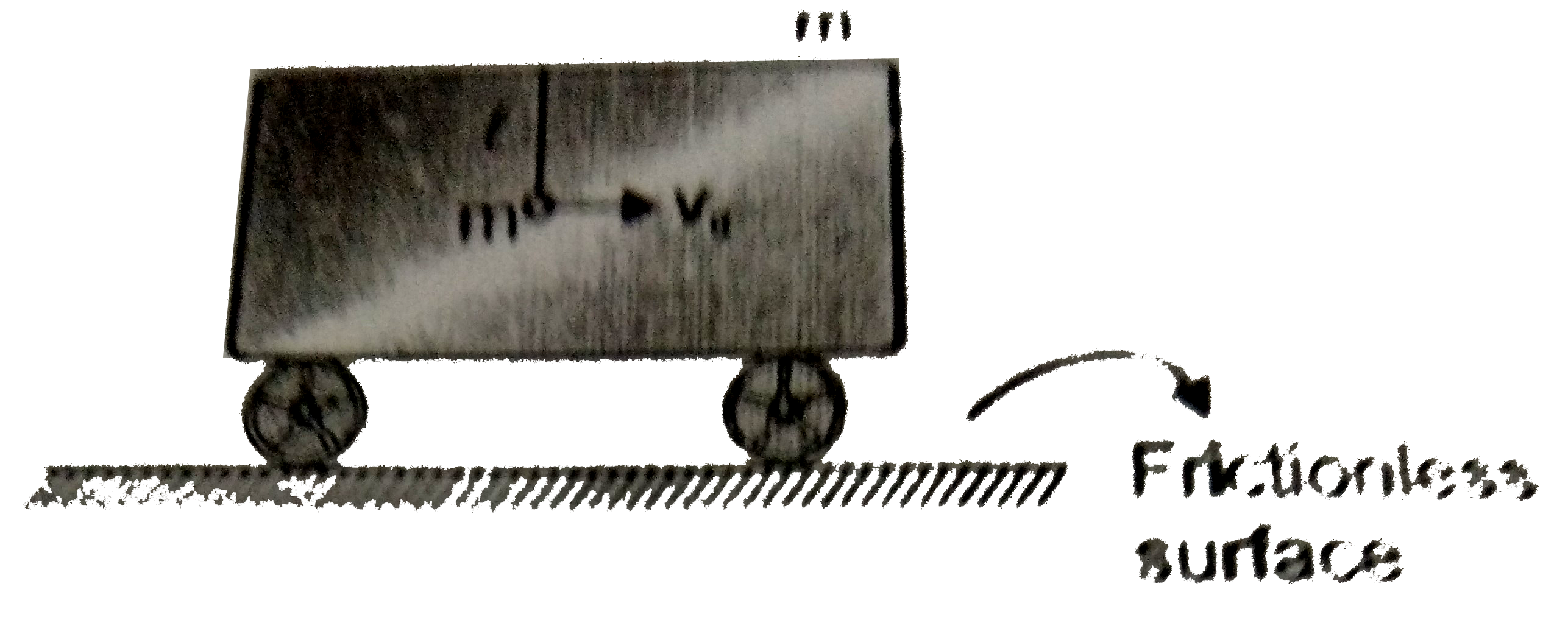 A2V20gBV20gCV204gDV202g
A2V20gBV20gCV204gDV202gA uniform rod AB of mass m is suspended in equilibrium from two similar springs as shown. If spring 2 breaks, then the angular acceleration of the bar at that instant will be
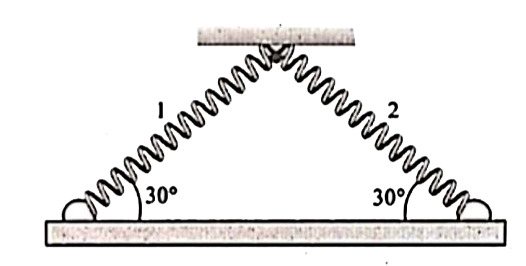 A2glB2g3lC3glDg3l
A2glB2g3lC3glDg3l
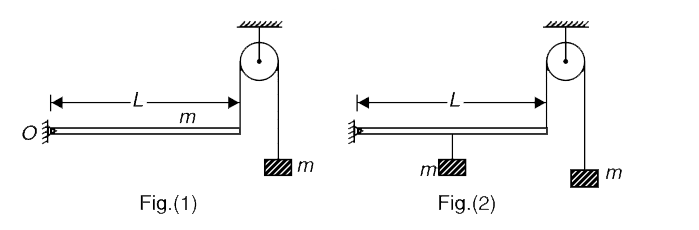
(a) In the system shown in figure 1, the uniform rod of length L and mass m is free to rotate in vertical plane about point O. The string an pulley are mass less. The block has mass equal to that of the rod. Find the acceleration of the block immediately after the system is released with rod in horizontal position.
(b) System shown in figure 2 is similar to that in figure 1 apart from the fact that rod is mass less and a block of mass m is attached to the centre of the rod with the help of a thread. Find the acceleration of both the blocks immediately after the system is released with rod in horizontal position.
View SolutionA solid sphere of mass m and radius R is placed over a plank of same mass m. There is sufficient friction between sphere and plank to prevent slipping.

When a horizontal force F is applied at centre of sphere, acceleration of the plank is
View SolutionTwo point masses, each of mass 'm' are connected to the end of spring. If force F is applied on one of the mass, then find the acceleration of this mass if the acceleration of other mass is a ?

View SolutionA uniform bar AB of mass m and a ball of the same mass are released from rest from the same horizontal position. The bar is hinged at end A. There is gravity downwards. What is the distance of the point from point B that has the same acceleration as the ball, immediately after release?

View SolutionThe string between blocks of mass m and 2m is massless and inextensible. The system is suspended by a massless spring as shown. If the string is cut find the magnitudes of accelerations of mass 2m and m (immediately after cutting)

View Solution
