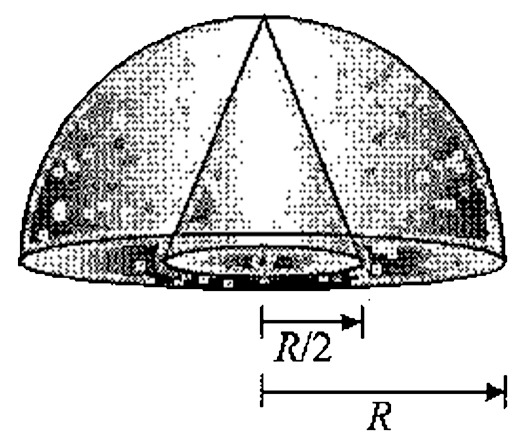
A uniform solid right circular cone of base radius R is joined to a uniform solid hemisphere of radius R and of the same density, as shown in the figure. The centre of mass of the.composite solid lies at the centre of base of the cone. The height of the cone is √xR. Find x.
'(##CEN_KSR_PHY_JEE_C08_E01_017_Q10##)'
The correct Answer is:3
Topper's Solved these Questions
Similar Questions
A uniform solid right circular cone of base radius R is joined to a uniform solid hemisphere of radius R and of the same density, as shown. The centre of mass of the composite solid lies at the centre of base of the cone. The height of the cone is

View SolutionA uniform solid hemisphere of radius r is joined to a uniform solid right circular cone of base radius r and height √3r. If both have same density, then find the position of centre of mass from centre of hemisphere
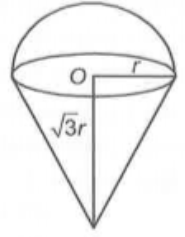
View Solution
Knowledge Check
A uniform solid right circular cone of base radius R is joined to a uniform solid hemisphere of radius R and of the same density, as shown. The centre of mass of the composite solid lies at the centre of base of the cone. The height of the cone is
 A1.5RB√3RC3RD2√3R
A1.5RB√3RC3RD2√3RA uniform solid right circular cone of base radius R is joined to a uniform solid hemisphere of radius R and of the same density, so as to have a common face. The centre of mass of the composite solid lies on the common face. The height of the cone is:
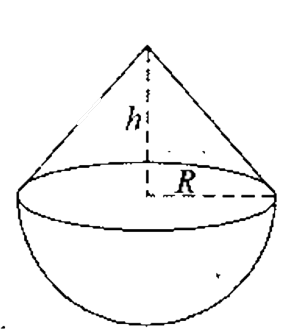 A1.5RB√3RC3RD2√3R
A1.5RB√3RC3RD2√3RA hemisphere and a solid cone have a common base. The center of mass of common structure coincides with the common base. If R is the radius of hemisphere and h is the height of the cone, then h/R will be
A√3B3C1√3D13
A uniform solid cone of height 40 cm is shown in figure. The distance of centre of mass of the cone from point B (centre of the base) is :
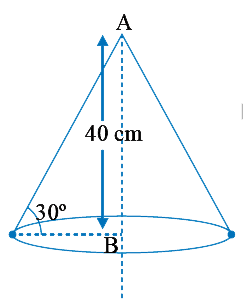
View SolutionA uniform solid cone of height 40 cm is shown in figure. The distance of centre of mass of the cone from point B (centre of the base) is :

View SolutionA uniform solid cone of height 40 cm is shown in figure. The distance of centre of mass of the cone from point B (centre of the base) is :
View SolutionFrom a hemisphere of radius R a cone of base radius R/w and height R is cut as shown in figure. Find the height of centre of mass of the remaining object.
View SolutionIf two solid hemispheres of same base radius r are joined together along their bases, then the curved surface area of the this new solid is
View Solution
