A uniform solid hemisphere of radius r is joined to a uniform solid right circular cone of base radius r and height √3r. If both have same density, then find the position of centre of mass from centre of hemisphere 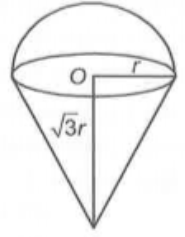A uniform solid hemisphere of radius r is joined to a uniform solid right circular cone of base radius r and height sqrt3r. If both have same density, then find the position of centre of mass from centre of hemisphere

A

r4 distance from O

B

At O

C

r2 distance from O

D

r3 distance from O

Video Solution
Doubtnut Promotions Banner
|
Answer

Step by step video & image solution for A uniform solid hemisphere of radius r is joined to a uniform solid right circular cone of base radius r and height sqrt3r. If both have same density, then find the position of centre of mass from centre of hemisphere by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023