A uniform sphere of mass m and radius R is placed on a rough horizontal surface [Fig.] The sphere is struck horizontally at a hight h from the floor. Match the following :
(A) h=R/2 (p) Sphere rolls without slipping with a constant velocity and no loss of energy.
(B) h=R (q) Sphere spins clockwise, loses energy by friction.
(C ) h=3R/2 (r) Sphere spins anti-clockwise, loses energy by friction.
(D) h=7R/5 (s) Sphere has only a translational motion, looses energy by friction.
![A uniform sphere of mass m and radius R is placed on a rough horizontal surface [Fig.] The sphere is struck horizontally at a hight h from the floor. Match the following : (A) h = R//2 (p) Sphere rolls without slipping with a constant velocity and no loss of energy. (B) h = R (q) Sphere spins clockwise, loses energy by friction. (C ) h = 3R//2 (r) Sphere spins anti-clockwise, loses energy by friction. (D) h = 7R//5 (s) Sphere has only a translational motion, looses energy by friction.](https://d10lpgp6xz60nq.cloudfront.net/physics_images/PR_XI_V01_C05_S01_303_Q01.png)
A -r, B - s, C - q, D - p
A - s, b - p, C - r, D - q
A - q, B - r, C - p, D - s
A - p, B - q, C - s, D - r
The correct Answer is:A
Let the sphere of mass M and radius R be struck horizontally at a height h from the floor, as shown in the figure.
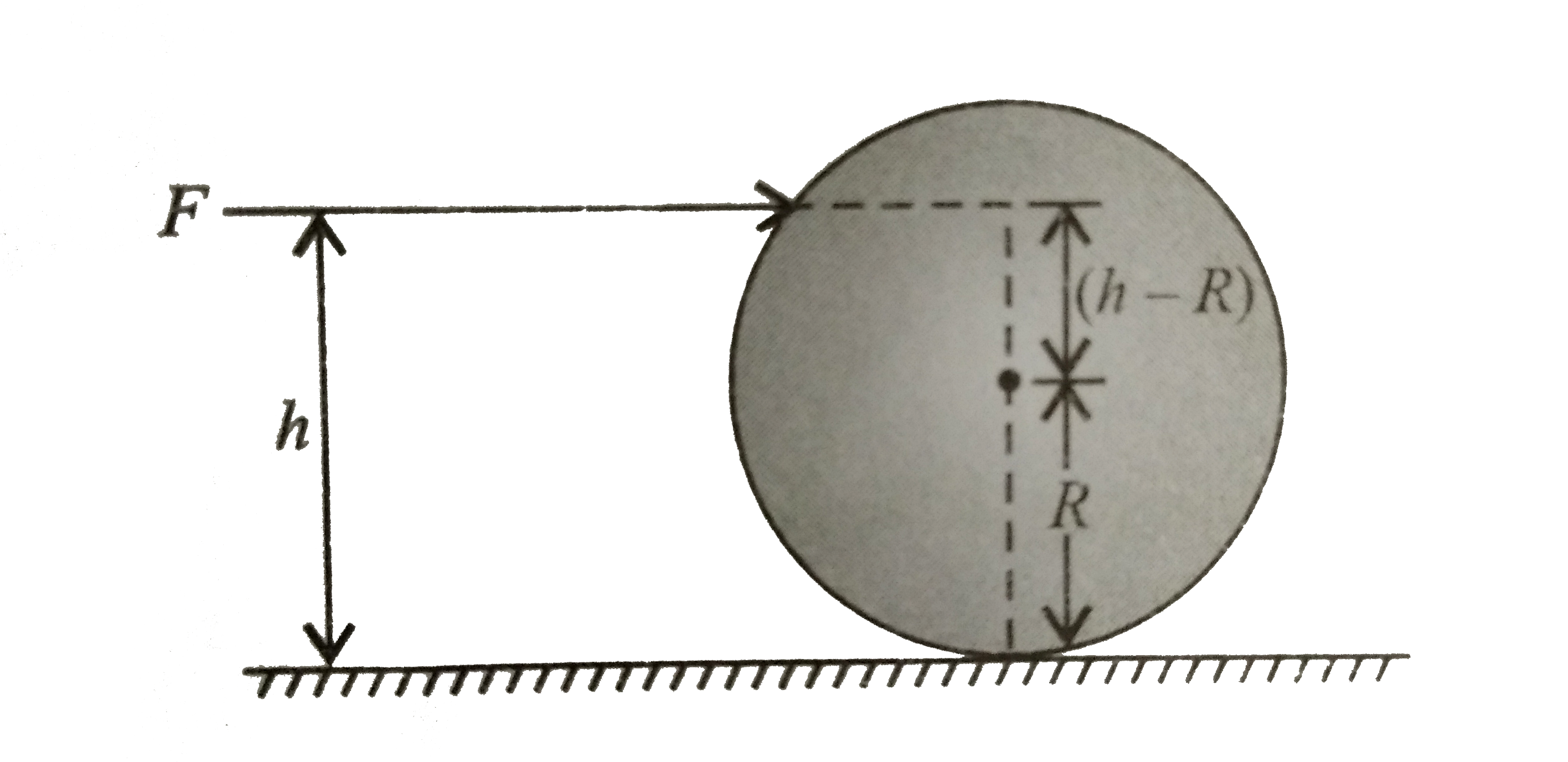
The sphere will roll without slipping when ω=vR
Angulmar momentum of sphere about its center of mass,
Mv(h−R)=Iω=(25MR2)(vR)
mv(h−R)=25MvR
h−R=25R or h=75R
∴ The sphere will roll without slipping with a consant velocity and no loss energy when h=75R
∴ The sphere will roll without slipping with a constant velocity and no less energy when h=75R
∴ D-p
Torque due to applied force about center of mass,
τ=F(h−R)
If τ=0,h=R, sphere will have only translational motion. It would lose energy by friction.
∴B−s
The sphere will spin clockwise, when τ is positive, i.e., h>R.
∴C−q
Again, the sphere will spin anticlockwise, when τ is negative, i.e., h<R
∴A−r
Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSBook:NCERT FINGERTIPSChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSExercise:Higher Order Thinking Skills
Explore 8 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSBook:NCERT FINGERTIPSChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSExercise:NCERT Exemplar
Explore 8 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSBook:NCERT FINGERTIPSChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSExercise:Angular Momentum In Case Of Rotations About A Fixed Axis
Explore 16 Videos
- PRACTICE PAPERSBook:NCERT FINGERTIPSChapter:PRACTICE PAPERSExercise:Practice Paper 3
Explore 50 Videos
- THERMAL PROPERTIES OF MATTERBook:NCERT FINGERTIPSChapter:THERMAL PROPERTIES OF MATTERExercise:Assertion And Reason
Explore 10 Videos
Similar Questions
A uniform sphere of mass m and radius R is placed on a rough horizontal surface [Fig.] The sphere is struck horizontally at a hight h from the floor. Match the following :
(a) h=R/2 (i) Sphere rolls without slipping with a constant velocity and no loss of energy.
(b) h=R (ii) Sphere spins clockwise, loses energy by friction.
(c ) h=3R/2 (iii) Sphere spins anti-clockwise, loses energy by friction.
(d) h=7R/5 (iv) Sphere has only a translational motion, looses energy by friction.

View SolutionA unifrom sphere of mass m and radius R is placed on a rough horizontal surface (figure) .the sphere is stuuck horizontally at a height h from the floor . Match the following

View Solution
Knowledge Check

A solid sphere of mass ma nd radis R is placed on a rough horizontal surface A horizontal force F is applied to sphere at a height h, (0≤h≤R) from centre. If sphere rolls slipping then,AThe maximum possible acceleration of sphere is FMBThe maximum possible acceleration of sphere is 10F7MCThe magnitude of friction force acting on the sphere is zero if h=2R5DThe magnitude of friction force acting on the sphere is zero h=3R4.A solid sphere of mass M and radius R is placed on a rough horizontal surface. It is stuck by a horizontal cue stick at a height h above the surface. The value of h so that the sphere performs pure rolling motion immediately after it has been stuck is
 A2R5B5R2C7R5D9R5
A2R5B5R2C7R5D9R5A uniform solid sphere of mass M and radius R is placed on a smooth horizontal surface. It is given a horizontal impulse J at a height h above the centre of mass and sphere starts rolling. Then the value of h and speed of ccentre of mass are
Ah=25Randv=JMBh=25Randv=25JMCh=75Randv=75JMDh=75Randv=JM
A uniform sphere of mass m and radius R is placed on a rough horizontal surface. The sphere is struck horizontally at a heighth from the floor. Match the following:

View SolutionA uniform sphere of mass m and radius R is placed on a rough horizontal surface. The spher is struck horizontally at a height h from the floor. Show that the sphere rolls without slipping with a constant velocity, when h=7R/5.
View SolutionA solid sphere of mass M and radius R is pulled horizontally on a rough surface as shown in Fig. Choose the incorrect alternatives.

View SolutionA sharp vertical impulse J is given to a uniform solid sphere of mass m and radius R place on a rough horizontal surface. Choose the correct options

View SolutionA solid sphere of mass M and radius R is placed on a smooth horizontal surface. It is given a horizontal impulse J at a height h above the centre of mass and sphere starts rolling then, the value of h and speed of centre of mass are –
View Solution
