A uniform sphere of mass m and radius R start rolling without slipping down an inclined plane. Find the time dependence of the angular. How will the result be affected in the case of a perfectly smooth inclined plane? The angle of inclination of the plane is θ.
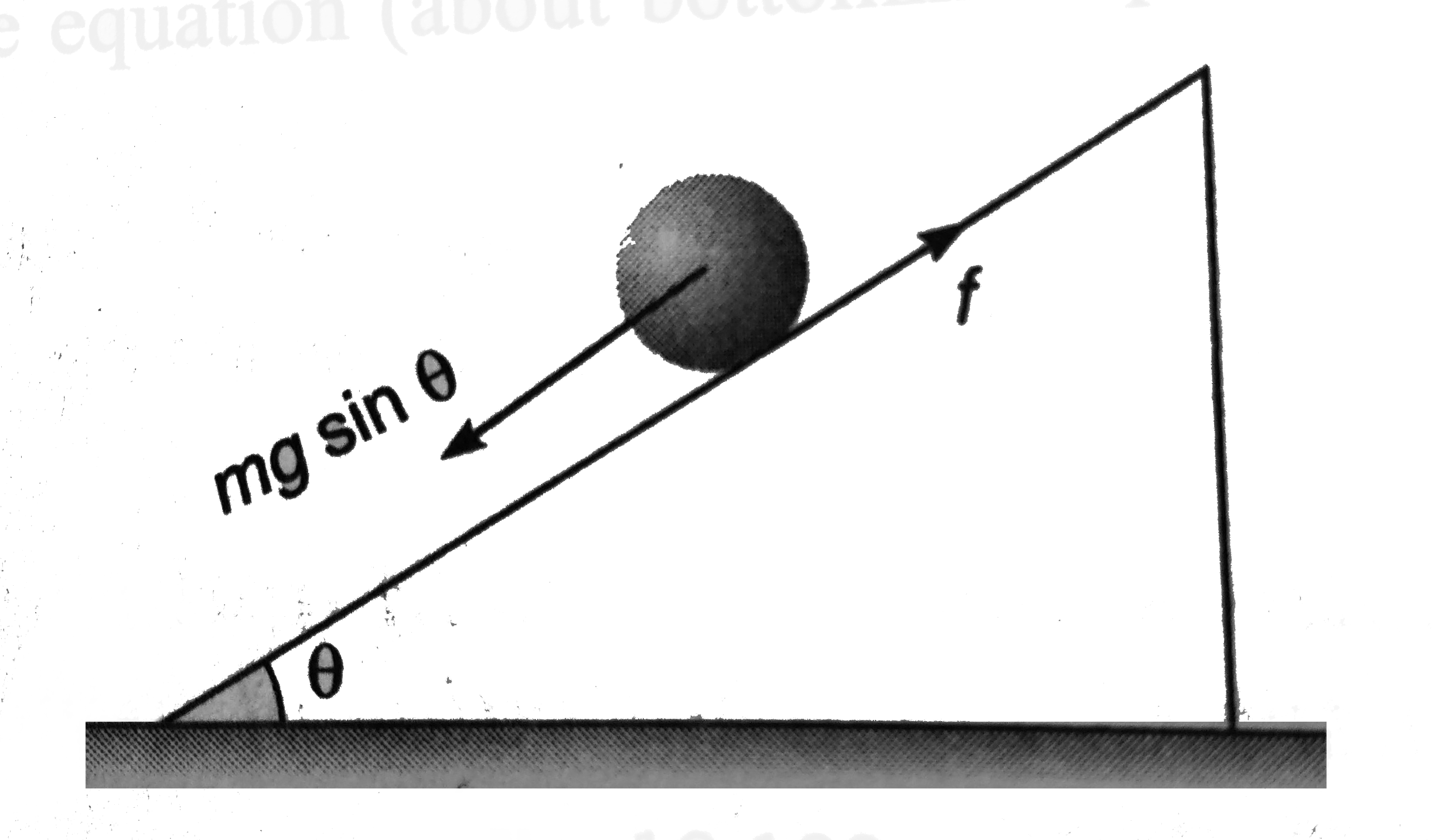
Applying the equation (about bottommost point)
Anuglar impulse = change in angular momentum about point of contact we have,
τ(mgsinθ0R= constant
∴ angular impulse =τ×t=(mgsinθ)Rt
or L=(mgsinθ)Rt
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Solved Examples25videos
ROTATIONAL MECHANICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Miscellaneous Examples2videos
ROTATIONAL MECHANICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises39videos
ROTATION
- BOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MOTIONEXERCISE - Integer Type Questions17videos
ROTATIONAL MOTION
Similar Questions
A spherical shell of mass m and radius R is rolling up without slipping on a rough inclined plane as shown in the figure. The direction of static friction acting on the shell is
View SolutionA solid sphere of mass m rolls without slipping on an inclined plane of inclination θ. The linear acceleration of the sphere is
View Solution
Knowledge Check
- Question 1 - Select One
A solid cylinder of mass M and radius R rolls without slipping down an inclined plane making an angle 6 with the horizontal. Then its acceleration is.
A1/3 g sinθB2/3 g sinθC2/5 g sinθD2/7 g sinθ
A hollow cylinder and a solid cylinder are rolling without slipping down an inclined plane, then which of these reaches earlier ?
View SolutionA drum of radius R and mass M, rolls down without slipping along an inclined plane of angle θ. The frictional force-
View SolutionA body is rolling down an inclined plane. Its acceleration will not depend on the following:
View SolutionA solid spherical ball is rolling without slipping down an inclined plane. The fraction of its total kinetic energy associated with rotation is
View SolutionA uniform sphere of mass m and radius R rolls without slipping down an inclined plane set at an angle θ to the horizontal. Find
(a) the friction coefficient at which slipping is absent,
(b) the kinetic energy of the sphere t seconds after the beginning of motion.View SolutionA hollow sphere of mass m starting from rest rolls without slipping, on an inclined plane of inclination What is the total energy of the sphere after 10−5s if after 10−5isv?
View SolutionThe acceleration of a body rolling down on an inclined plane does not depend upon
View Solution

