A uniform square plate and a disc having same mass per unit area are kept in contact as shown in Fig. The side of square and diameter of circle are both equal to $L$ . Locate the position of centre of mass of the system w.r.t. the centre of the square.

Video Solution

Text Solution

Verified by Experts

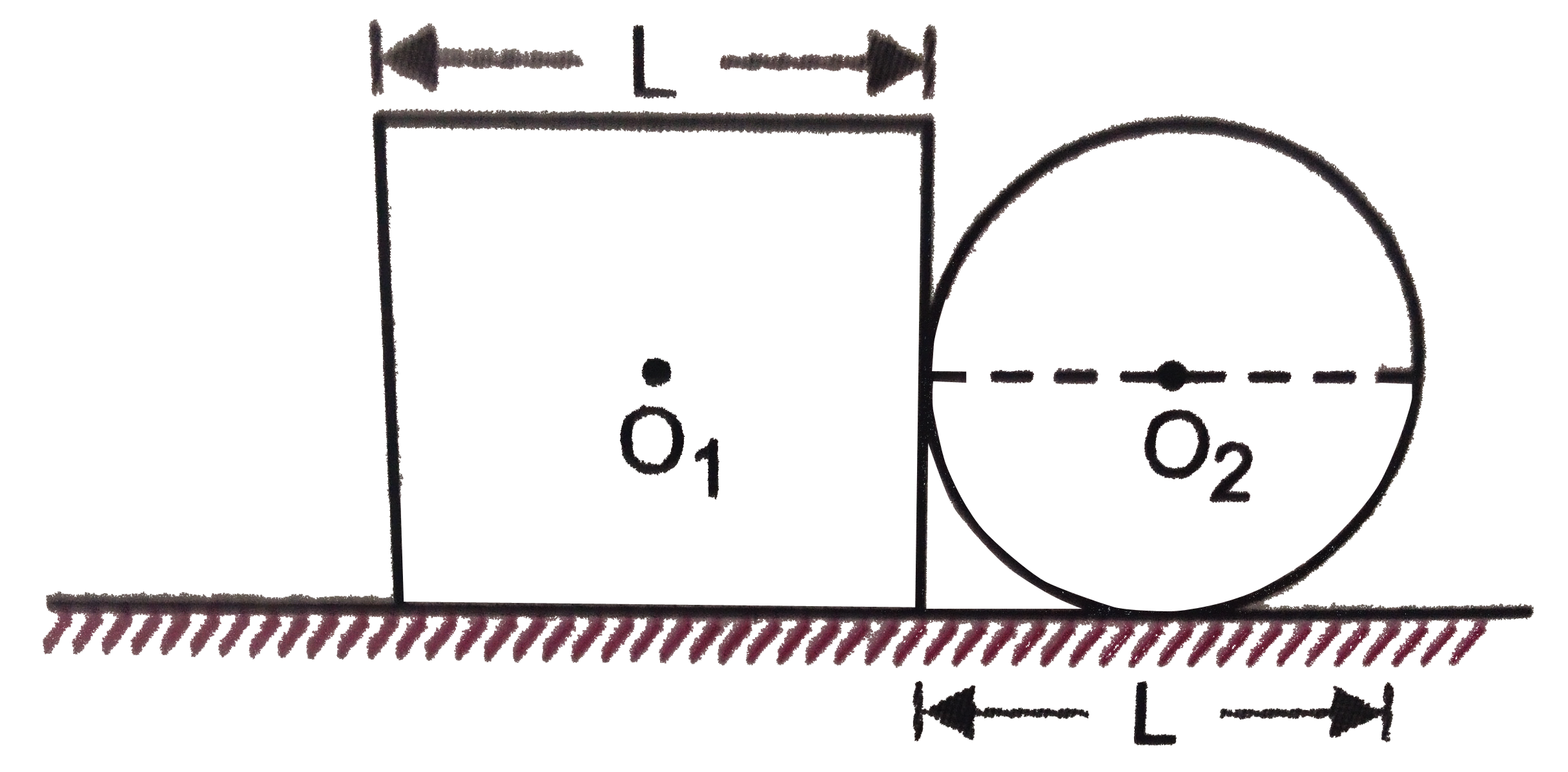
Let mass per unit area of the square plate = mass per unit area of disc $= σ$
$∴$ Mass of square plate
$m_{1} = σ L^{2}$ , and mass of disc
$m_{2} = (π r^{2}) σ = (π \frac{L^{2}}{4}) σ$
Centre of square is $O_{1}$ , where $m_{1}$ is concentrated and centre of disc is $O_{2}$ , where $m_{2}$ is concentrated. If $x$ is distance of c.m of the combination from $O_{1}$ , then
$x_{c m} = \frac{m_{1} x_{1} + m_{2} x_{2}}{m_{1} + m_{2}} = \frac{m_{1} \times 0 + m_{2} L}{m_{1} + m_{2}}$
$= \frac{(π \frac{L^{2}}{4}) σ \times L}{σ L^{2} + \frac{π L^{2} σ}{4}} = \frac{σ π L^{2} / 4 \times L}{σ L^{2} (1 + π / 4)}$
$x_{c m} = \frac{π / 4 \times L}{(4 + π) / 4} = (\frac{π L}{4 + π})$

Updated on:21/07/2023

The side of a square is equal to the diameter of a circle. If the side and radius change at the same rate, then the ratio of the change of their areas, is
A $1 : π$
B $π : 1$
C $2 : π$
D $1 : 2$
Four particles each of mass m are placed at the vertices of a square of side $l$ . the potential at the centre of square is
A $- 2 \sqrt{2} \frac{G m}{l}$
B $- 3 \sqrt{2} \frac{G m}{l}$
C $- 2 \frac{G m}{l}$
D $- 4 \sqrt{2} \frac{G m}{l}$
A circular plate of diameter d is kept in contact with a square plate of edge d as shown in figure. The densities of the material and the thickness are same
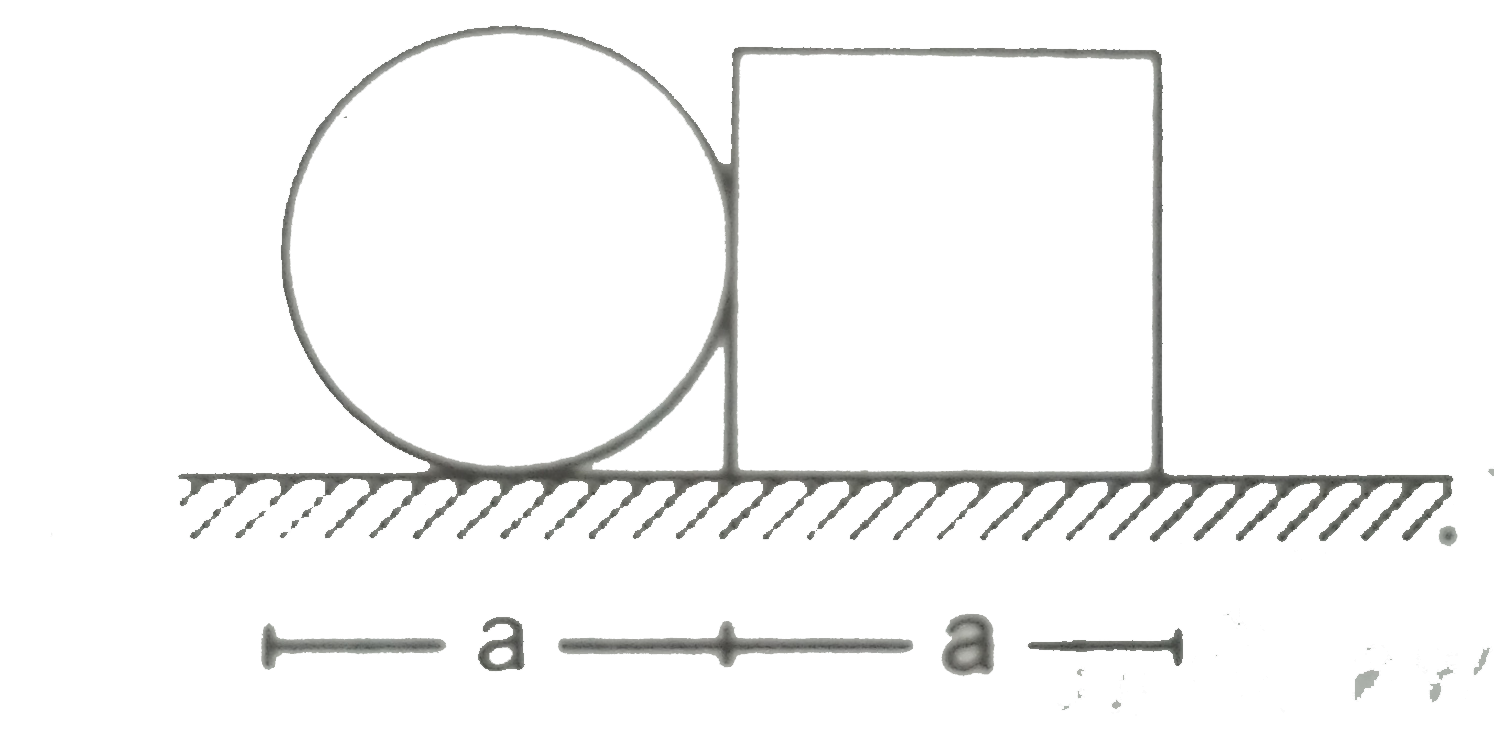. Everywhere. The centre of mass of the composite system will be
Ainside the circular plate
Binside hte square plate
Cat the point of contact
Doutside the system