A uniform thin bar of mass 6m and length 12L is bend to make a regular hexagon. Its moment of inertia about an axis passing through the centre of mass and perpendicular to the plane of the hexagon is :
20mL2
6mL2
125mL2
30mL2
The correct Answer is:A
To find the moment of inertia of a uniform thin bar bent into a regular hexagon, we can follow these steps:
Step 1: Determine the Length of Each Side of the Hexagon
Given that the total length of the bar is 12L and it is bent to form a regular hexagon, we can find the length of each side of the hexagon.
Length of each side=Total length6=12L6=2L
Step 2: Calculate the Distance from the Center of Mass to Each Side
For a regular hexagon, the distance from the center to the midpoint of any side can be calculated using trigonometry. The angle at the center corresponding to each side is 60∘.
Using the tangent function:
tan(60∘)=oppositeadjacent=rL
Where r is the distance from the center of the hexagon to the midpoint of a side, and L is half the length of a side.
Thus,
r=Ltan(60∘)=L⋅√3=√3L
Step 3: Calculate the Moment of Inertia
The moment of inertia I about an axis passing through the center of mass and perpendicular to the plane of the hexagon can be calculated using the formula:
I=∑(mir2i)
Where mi is the mass of each side and ri is the distance from the center of mass to the side.
Since the total mass of the bar is 6m and it is divided into 6 equal parts (one for each side of the hexagon):
mi=6m6=m
Now substituting the values:
I=6(m(2L2)2)+6(m(√3L)2)
=6(m⋅(2L)2⋅13)+6(m⋅3L2)
=6(4mL23)+6(3mL2)
=8mL2+18mL2=26mL2
Final Calculation
The moment of inertia about the center of mass and perpendicular to the plane of the hexagon is:
I=20mL2
Answer
Thus, the moment of inertia about an axis passing through the center of mass and perpendicular to the plane of the hexagon is 20mL2.
---
Given that the total length of the bar is 12L and it is bent to form a regular hexagon, we can find the length of each side of the hexagon.
For a regular hexagon, the distance from the center to the midpoint of any side can be calculated using trigonometry. The angle at the center corresponding to each side is 60∘.
tan(60∘)=oppositeadjacent=rL
Where r is the distance from the center of the hexagon to the midpoint of a side, and L is half the length of a side.
r=Ltan(60∘)=L⋅√3=√3L
The moment of inertia I about an axis passing through the center of mass and perpendicular to the plane of the hexagon can be calculated using the formula:
I=∑(mir2i)
Where mi is the mass of each side and ri is the distance from the center of mass to the side.
mi=6m6=m
I=6(m(2L2)2)+6(m(√3L)2)
=6(m⋅(2L)2⋅13)+6(m⋅3L2)
=6(4mL23)+6(3mL2)
=8mL2+18mL2=26mL2
The moment of inertia about the center of mass and perpendicular to the plane of the hexagon is:
I=20mL2
Thus, the moment of inertia about an axis passing through the center of mass and perpendicular to the plane of the hexagon is 20mL2.
Topper's Solved these Questions
- ROTATIONAL MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MOTIONEXERCISE - A Only One Option is Correct
86 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MOTIONEXERCISE - More than one option is correct
36 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Subjective Questions
2 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBOOK - DC PANDEY ENGLISHCHAPTER - SEMICONDUCTORS AND ELECTRONIC DEVICESEXERCISE - More than One Option is Correct
3 Videos
Similar Questions
For the same total mass, which of the following will have the largest moment of inertia about an axis passing through the centre of mass and perpendicular to the plane of the body
View SolutionMoment of inertia of a ring of mass M and radius R about an axis passing through the centre and perpendicular to the plane is
View SolutionThe moment of inertia of a copper disc, rotating about an axis passing through its centre and perpendicular to its plane
View SolutionA uniform equilateral triangular lamina of side a has mass m. Its moment of inertia about the axis passing through the centroid and prependicular to the plane of the lamina is :-
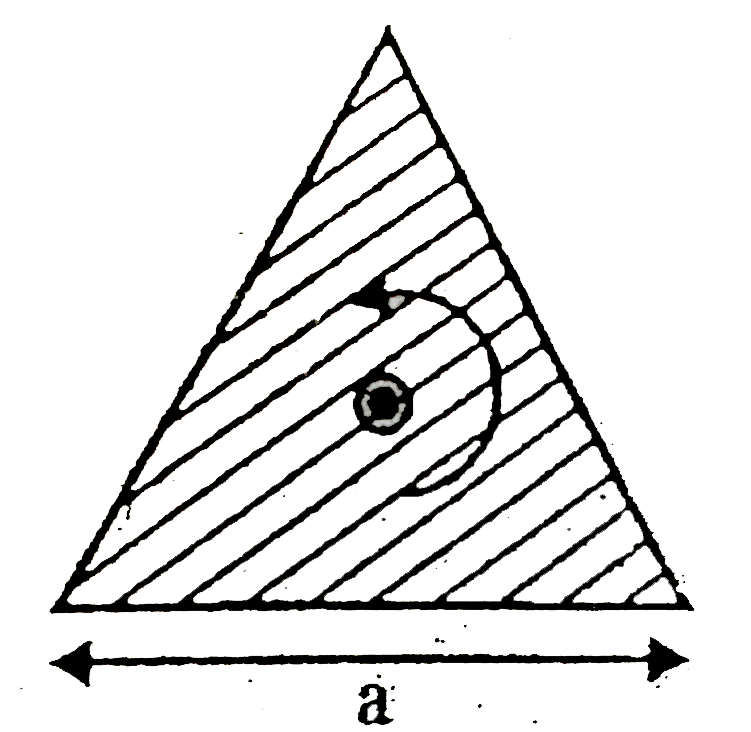
View SolutionA thin uniform wire of mass m and length l is bent into to shape of a semicircle. The moment of inertia of that wire about an axis passing through its free ends is
View SolutionFour identical thin rods each of mass M and length l, from a square frame. Moment of inertia of this frame about an axis through the centre of the square and perpendicular to its plane is
View SolutionTwo rods each of mass m and length 1 are joined at the centre to form a cross. The moment of inertia of this cross about an axis passing through the common centre of the rods and perpendicular to the plane formed by them, is :
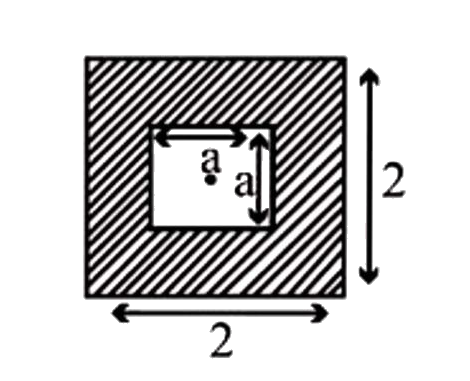
View SolutionA square of a side a is cut from a square of side 2a as shown in the figure. Mass of this square with a hole is M. Then its moment of inertia about an axis passing through its centre of mass and perpendicular to its plane will be
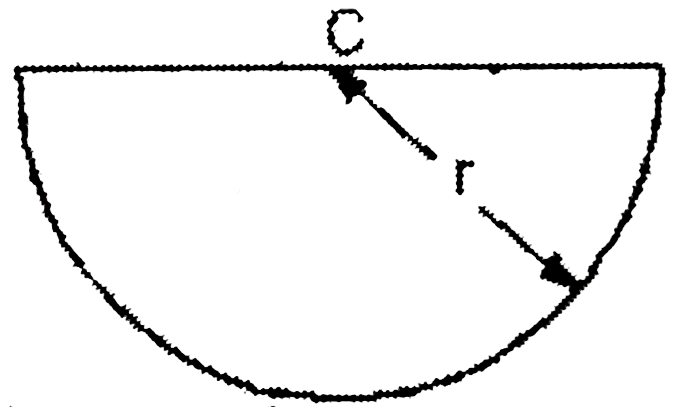
View SolutionA semicircular lamina of mass m and radius r and centre C. Its center of mass is at a distance x from C. Its moment of inertia about an axis through its center of mass and perpendicular to its plane is:
View SolutionFind the moment of inertia of a uniform cylinder about an axis through its centre of mass and perpendicular to its base. Mass of the cylinder is M and radius is R.
View Solution
