A uniform thin cylindrical disk of mass M and radius R is attaached to two identical massless springs of spring constatn k which are fixed to the wall as shown in the figure. The springs are attached to the axle of the disk symmetrically on either side at a distance d from its centre. The axle is massless and both the springs and the axle are in horizontal plane. the unstretched length of each spring is L. The disk is initially at its equilibrium position with its centre of mass (CM) at a distance L from the wall. The disk rolls without slipping with velocity ${\vec{V}}_{0} = v a c V_{0} \hat{i} .$ The coefficinet of friction is $μ .$

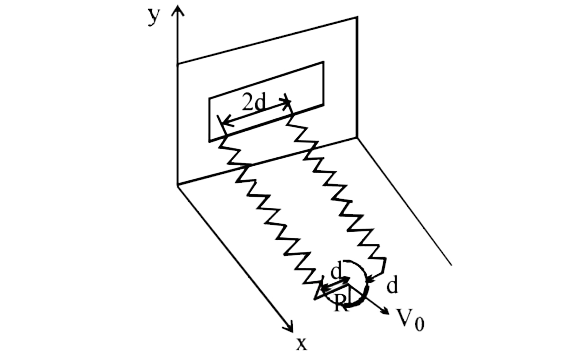
The centre of mass of the disk undergoes simple harmonic motion with angular frequency $ω$ equal to -

$\sqrt{\frac{k}{M}}$

$\sqrt{\frac{2 k}{M}}$

$\sqrt{\frac{2 K}{3 M}}$

$\sqrt{\frac{4 K}{3 M}}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

From the previous question $a = - \frac{4 k x}{3 M}$
Comparing with $a = - ω^{2} x,$ we get
$ω = \sqrt{\frac{4 k}{3 M}}$

Class 11 PHYSICS RIGID BODY DYNAMICS

Topper's Solved these Questions

Knowledge Check

A uniform thin cylindrical disk of mass M and radius R is attaached to two identical massless springs of spring constatn k which are fixed to the wall as shown in the figure. The springs are attached to the axle of the disk symmetrically on either side at a distance d from its centre. The axle is massless and both the springs and the axle are in horizontal plane. the unstretched length of each spring is L. The disk is initially at its equilibrium position with its centre of mass (CM) at a distance L from the wall. The disk rolls without slipping with velocity ${\to V}_{0} = v a c V_{0} ˆ i .$ The coefficinet of friction is $μ .$

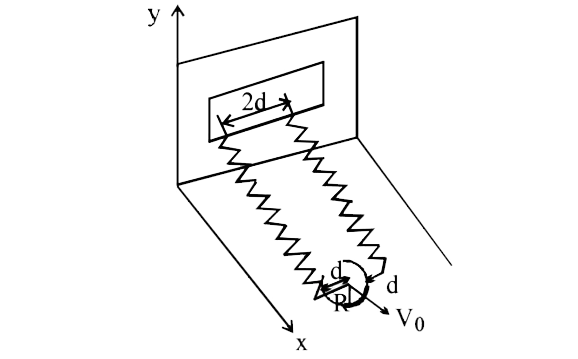
The maximum value of $V_{0}$ for whic the disk will roll without slipping is-
A $μ g \sqrt{\frac{M}{k}}$
B $μ g \sqrt{\frac{M}{2 k}}$
C $μ g \sqrt{\frac{3 M}{k}}$
D $μ g \sqrt{\frac{5 M}{2 k}}$
A uniform thin cylindrical disk of mass M and radius R is attaached to two identical massless springs of spring constatn k which are fixed to the wall as shown in the figure. The springs are attached to the axle of the disk symmetrically on either side at a distance d from its centre. The axle is massless and both the springs and the axle are in horizontal plane. the unstretched length of each spring is L. The disk is initially at its equilibrium position with its centre of mass (CM) at a distance L from the wall. The disk rolls without slipping with velocity ${\to V}_{0} = v a c V_{0} ˆ i .$ The coefficinet of friction is $μ .$

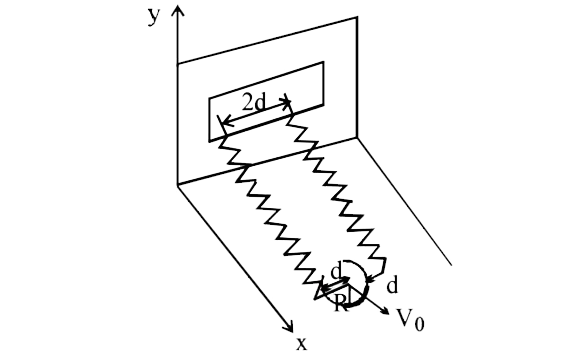
The net external force acting on the disk when its centre of mass is at displacement x with respect to its equilibrium position is.
A $= - k x$
B $- 2 k x$
C $- 2 k x / s$
D $- 4 k x / 3$
A particle of mass m is attached to three identical massless springs of spring constant k as shown in the m 135 figure. The time period of vertical oscillation of the particle is

A $2 π \sqrt{\frac{m}{k}}$
B $2 π \sqrt{\frac{m}{2 k}}$
C $2 π \sqrt{\frac{m}{3 k}}$
D $π \sqrt{\frac{m}{k}}$