A bob of mass m is connected to a spring of spring constant k and a string which is fixed to the ceiling as shown in figure. Original length of the spring is L and the bob rotates in a horizontal circle centred at the fixed rod. Assuming the spring remains horizontal, then elongation in the spring is :

(mg−mω2L)tanθmω2+k
mgtanθ+mω2Lmω2−k
mgtanθ+mω2Lk
gtanθ−ω2Lω2−k/m
The correct Answer is:D
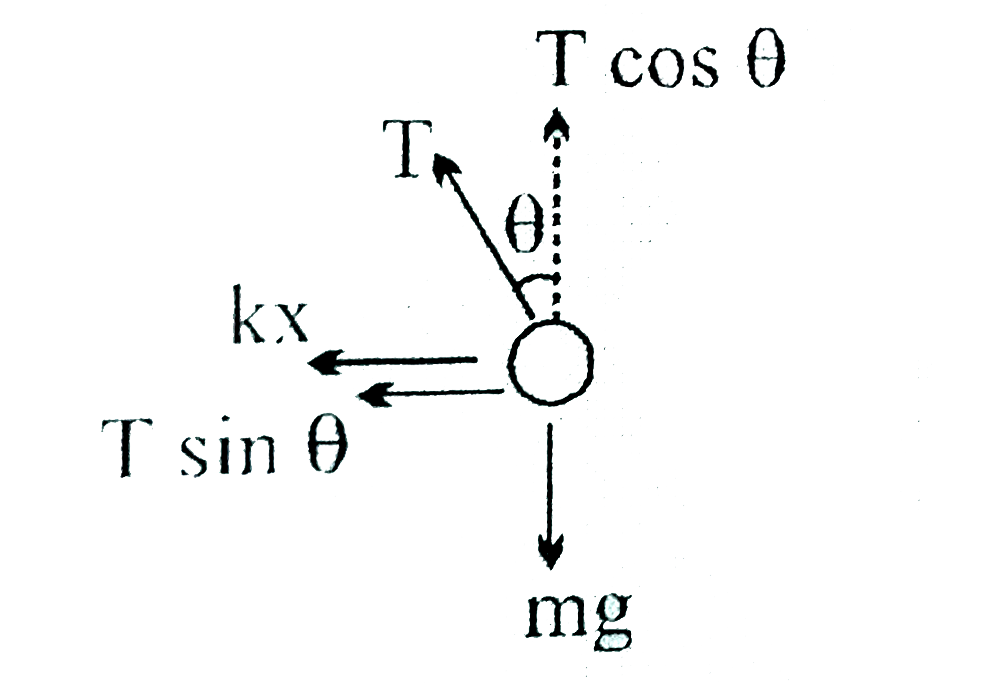
Tcosθ=mg … (i)
T=sinθ+kx=mw2(L+x) .. (2)
from (1) and (2)
x=gtanθ−ω2Lω2−km
Topper's Solved these Questions
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART (A)
32 Videos
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART (B)
3 Videos
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART- C
4 Videos
- SEMICONDUCTORSBOOK - BANSALCHAPTER - SEMICONDUCTORSEXERCISE - CBSE Question
32 Videos
Similar Questions
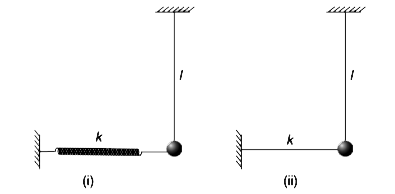
A simple pendulum of length L has a bob of mass m. The bob is connected to light horizontal spring of force constant k. The spring is relaxed when the pendulum is vertical (see fig (i)).
(a) The bob is pulled slightly and released. Find the time period of small oscillations. Assume that the spring remains horizontal.
(b) The spring is replaced with an elastic cord of force constant k. The cord is relaxed when the pendulum is vertical (see fig (ii)). The bob is pulled slightly and released. Find the time period of oscillations.
View Solution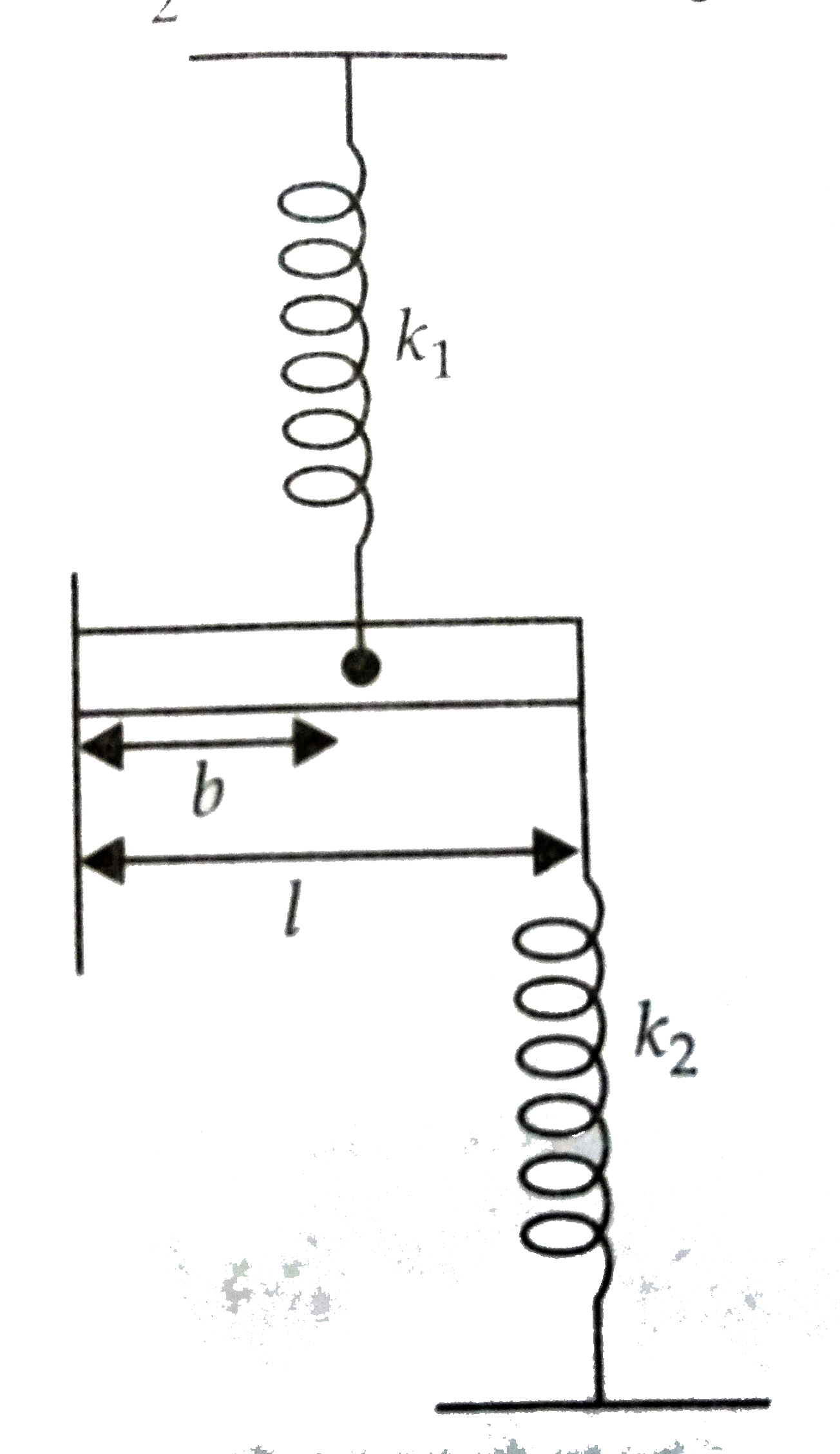
A rod of mass m and length l is connected by two spring of spring constants k1andk2, so that it is horizontal at equilibrium. What is the natural frequency of the system?
View Solution
Knowledge Check
A block of mass m is connected to two indentical springs of spring constant k which are in turn connected to fixed supports as shown in the figure. Find the time period for small oscillations of the block.
 A2π√mkB2π√m2kC2π√2mkDπ√m2k
A2π√mkB2π√m2kC2π√2mkDπ√m2kTwo blocks, of masses M and 2M, are connected to a light spring of spring constant K that has one end fixed, as shown in figure. The horizontal surface and the pulley are frictionless. The blocks are released from when the spring is non deformed. The string is light.
 .AMaximum extension in the spring is 4MgK.BMaximum kinetic energy of the system is 2M2g2K.CMaximum energy stored in the spring is four times that of maximum kinetic energy of the system.DWhen kinetic energy of the system is maximum energy stored in the spring is 4M2g2K.
.AMaximum extension in the spring is 4MgK.BMaximum kinetic energy of the system is 2M2g2K.CMaximum energy stored in the spring is four times that of maximum kinetic energy of the system.DWhen kinetic energy of the system is maximum energy stored in the spring is 4M2g2K.

A rod of mass m and length l is connected by two spring of spring constants k1andk2, so that it is horizontal at equilibrium. What is the natural frequency of the system?
View Solution
A ring of mass m is attached to a horizontal spring of spring constant k and natural length l0. The other end of the spring is fixed and the ring can slide on a horizontal rod as shown. Now the ring is shifted to position B and released Find the speed of the ring when the spring attains its natural length.
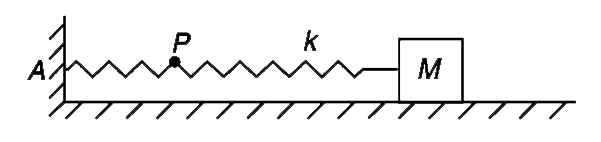
View SolutionA block of mass M is tied to a spring of force constant k and placed on a smooth horizontal surface. The natural length of the spring is L. P is a point on the spring at a distance L4 from its fixed end. The block is set in oscillations with amplitude A. Find the maximum speed of point P on the spring.
View SolutionTwo blocks, of masses M and 2M, are connected to a light spring of spring constant K that has one end fixed, as shown in figure. The horizontal surface and the pulley are frictionless. The blocks are released from when the spring is non deformed. The string is light.
 .
.
View SolutionTwo blocks, of masses M and 2M, are connected to a light spring of spring constant K that has one end fixed, as shown in figure. The horizontal surface and the pulley are frictionless. The blocks are released from when the spring is non deformed. The string is light.
 .
.
View SolutionA particle of mass m is moving with a constant speed v in a circular path in a smooth horizontal plate (plan of the paper ) by a spring force as shown in figure If the natural length of the spring is l0 and stiffeness of the spring is k find the elongation of the spring

View Solution
