A uniform thin rope of length 12 m and mass 6 kg hangs vertically from a rigid support and block of mass 2kg is attached to its free end. A transverse short wave-train of wavelength 6 cm is produced at the lower end of the rope. What is the wavelength of the wavetrain (in cm) when it reaches the top of the rope?
As the rope has a mass and a mass is also suspended from the lower end, the tension in the rope will be different at different points. Now as v=√(T/m)
or vTvB=√TTTB=√(6=2)g2g=2(or)[frλTfbλB]=2
[asv=fλ]
Here fT=fB as frequency is the characteristic of the source producing the waves.
So λT=2λB=2×0.06=0.12m

Topper's Solved these Questions
- WAVE MOTION AND SOUNDBOOK - AAKASH SERIESCHAPTER - WAVE MOTION AND SOUNDEXERCISE - EXERCISE (LONG ANSWER QUESTIONS)
5 Videos
- WAVE MOTION AND SOUNDBOOK - AAKASH SERIESCHAPTER - WAVE MOTION AND SOUNDEXERCISE - EXERCISE (SHORT ANSWER QUESTIONS)
13 Videos
- WAVE MOTIONBOOK - AAKASH SERIESCHAPTER - WAVE MOTIONEXERCISE - PRACTICE SHEET ADVANCED (INTEGER TYPE QUESTIONS)
10 Videos
- WAVE OPTICSBOOK - AAKASH SERIESCHAPTER - WAVE OPTICSEXERCISE - PROBLEMS (LEVEL - II)
33 Videos
Similar Questions
A uniform rope of length 12 mm and mass 6 kg hangs vertically from a rigid support. A block of mass 2 kg is attached to the free end of the rope. A transverse pulse of wavelength 0.06 m is produced at the lower end of the rope. What is the wavelength of the pulse when it reaches the top of the rope?
View SolutionA uniform rope of length 12 mm and mass 6 kg hangs vertically from a rigid support. A block of mass 2 kg is attached to the free end of the rope. A transverse pulse of wavelength 0.06 m is produced at the lower end of the rope. What is the wavelength of the pulse when it reaches the top of the rope?
View Solution
Knowledge Check
A uniform rope of length 12 mm and mass 6 kg hangs vertically from a rigid support. A block of mass 2 kg is attached to the free end of the rope. A transverse pulse of wavelength 0.06 m is produced at the lower end of the rope. What is the wavelength of the pulse when it reaches the top of the rope?
A0.06 mB0.03 mC0.12 mD0.09 m
A uniform rope of length 10 cm and mass 4 kg hangs vertically from a rigid support. A block of mass 2 kg is attached to the free end of the rope. A transverse pulse of wavelength 0.06 m is produced at the lower end of the rope, what is the wavelength of the pulse when it reaches the top of the rope?
View SolutionA uniform rope of legnth L and mass m1 hangs vertically from a rigid support. A block of mass m2 is attached to the free end of the rope. A transverse pulse of wavelength λ1 is produced at the lower end of the rope. The wavelength of the pulse when it reaches the top of the rope is λ2. The ratio λ2λ1 is
View SolutionA uniform rope of elngth l and mass m hangs vertically from a rigid support. A block of mass m is attached to the free end of the rope. A transverse pulse of wavelength λ is produced at the lower end of the rope. The wavelength of the pulse, when it reaches the top of the rope. is aλ. Find a2
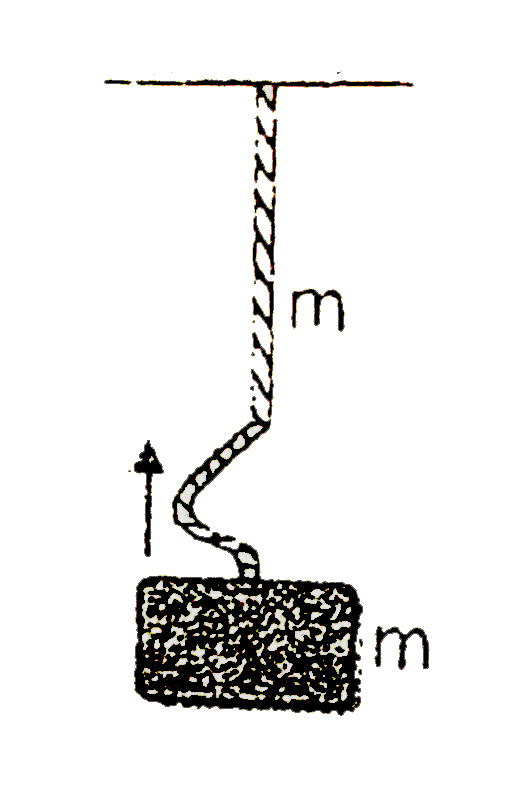
View SolutionA metal wire of length L is suspended vertically from a rigid support. When a bob of mass M is attached to the lower end of wire, the elongation of the wire is l:
View SolutionA uniform rope of length 12 m and mass 4 kg is hung vertically from a rigid support transverse wave pulse is produced at lower end. The speed of the wave pulse al x = 2.5 m from lower and will be kg=10 m/s)
View SolutionA thick uniform rope of length L is hanging from a rigid support. A transverse wave of wavelength λ0 is set up in the middle of the rope. The wavelength of the wave as it reaches the top most point is
View SolutionA mass of 2kg suspended by string of mass 6kg. A wave of wavelength 6 cm is produced at bottom of string. Wavelength of wave at top end of string will be
View Solution
