A mass of 2kg suspended by string of mass 6kg. A wave of wavelength 6 cm is produced at bottom of string. Wavelength of wave at top end of string will be
6 cm
18 cm
12 cm
24 cm
The correct Answer is:C
To solve the problem step by step, we need to analyze the situation involving the mass, the string, and the wave properties.
Step 1: Understand the system
We have a mass m=2kg suspended by a string of mass M=6kg. A wave of wavelength λA=6cm is produced at the bottom of the string.
Step 2: Calculate the tension at the bottom of the string
At the bottom of the string (point A), the tension TA is equal to the weight of the suspended mass:
TA=m⋅g=2kg⋅9.8m/s2=19.6N≈20N
Step 3: Calculate the tension at the top of the string
At the top of the string (point B), the tension TB must support both the weight of the mass and the weight of the string itself. The total weight supported at point B is:
Total weight=m⋅g+M⋅g=(2kg+6kg)⋅g=8kg⋅9.8m/s2=78.4N≈80N
Step 4: Relate the velocities and tensions
The wave velocity in a string is given by:
v=√Tμ
where T is the tension and μ is the mass per unit length. Since the mass of the string is distributed along its length, we can express the mass per unit length as μ=ML, where L is the length of the string.
Step 5: Relate the wavelengths using the velocities
Since the frequency f of the wave remains constant, we can relate the velocities and wavelengths at points A and B:
vBvA=λBλA
Using the relationship between velocity and tension:
vBvA=√TBTA
Step 6: Substitute the tensions
Substituting the values of tensions:
vBvA=√TBTA=√80N20N=√4=2
Step 7: Calculate the wavelength at the top of the string
Now, substituting into the wavelength relationship:
λBλA=2⟹λB=2⋅λA
Given λA=6cm:
λB=2⋅6cm=12cm
Final Answer
The wavelength of the wave at the top of the string is λB=12cm.
---
We have a mass m=2kg suspended by a string of mass M=6kg. A wave of wavelength λA=6cm is produced at the bottom of the string.
At the bottom of the string (point A), the tension TA is equal to the weight of the suspended mass:
TA=m⋅g=2kg⋅9.8m/s2=19.6N≈20N
At the top of the string (point B), the tension TB must support both the weight of the mass and the weight of the string itself. The total weight supported at point B is:
Total weight=m⋅g+M⋅g=(2kg+6kg)⋅g=8kg⋅9.8m/s2=78.4N≈80N
The wave velocity in a string is given by:
v=√Tμ
where T is the tension and μ is the mass per unit length. Since the mass of the string is distributed along its length, we can express the mass per unit length as μ=ML, where L is the length of the string.
Since the frequency f of the wave remains constant, we can relate the velocities and wavelengths at points A and B:
vBvA=λBλA
Using the relationship between velocity and tension:
vBvA=√TBTA
Substituting the values of tensions:
vBvA=√TBTA=√80N20N=√4=2
Now, substituting into the wavelength relationship:
λBλA=2⟹λB=2⋅λA
Given λA=6cm:
λB=2⋅6cm=12cm
The wavelength of the wave at the top of the string is λB=12cm.
Topper's Solved these Questions
Similar Questions
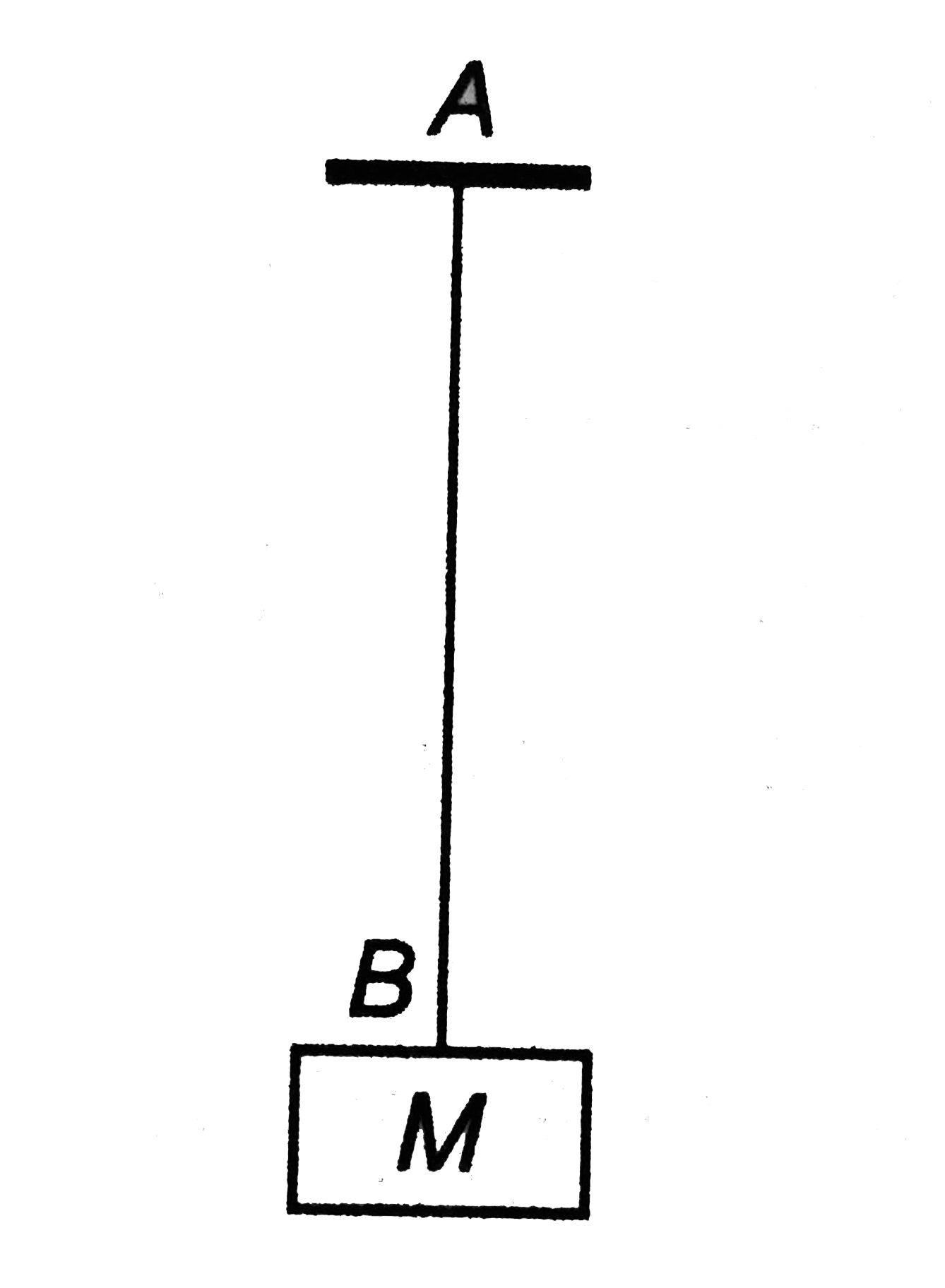
A block of mass M=2kg is suspended from a string AB of mass 6kg as shown in figure. A transverse wave pulse of wavelength λ0 is produced at point B. find its wavelength while reaching at point A.
View SolutionA uniform rope of length 12 mm and mass 6 kg hangs vertically from a rigid support. A block of mass 2 kg is attached to the free end of the rope. A transverse pulse of wavelength 0.06 m is produced at the lower end of the rope. What is the wavelength of the pulse when it reaches the top of the rope?
View Solution
Knowledge Check
A uniform rope of length 12 mm and mass 6 kg hangs vertically from a rigid support. A block of mass 2 kg is attached to the free end of the rope. A transverse pulse of wavelength 0.06 m is produced at the lower end of the rope. What is the wavelength of the pulse when it reaches the top of the rope?
A0.06 mB0.03 mC0.12 mD0.09 mA string of mass 3 kg is under tension of 400 N. the length of the stretched string is 25 cm. if the transverse jerk is stuck at one end of the string how long does the disturbance take to reach the other end?
A0.043sB4.33SC0.055 sD0.034 s
A uniform rope of length 12 mm and mass 6 kg hangs vertically from a rigid support. A block of mass 2 kg is attached to the free end of the rope. A transverse pulse of wavelength 0.06 m is produced at the lower end of the rope. What is the wavelength of the pulse when it reaches the top of the rope?
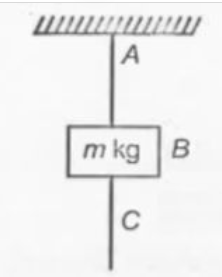
View SolutionA mass of 1 kg is suspended by a string A . Another string C its connected to its lower end. If a sudden jark is given to C then
View SolutionA uniform rope of length 10 cm and mass 4 kg hangs vertically from a rigid support. A block of mass 2 kg is attached to the free end of the rope. A transverse pulse of wavelength 0.06 m is produced at the lower end of the rope, what is the wavelength of the pulse when it reaches the top of the rope?
View SolutionA string is suspended from the ceiling. A wave train is produced at the bottom at regular interval. As the wave moves upwards

View SolutionA harmonic wave is travelling along +ve x-axis, on a stretched string. If wavelength of the wave gets doubled, then
View SolutionA standing wave is produced on a string on a string clamped at one end and free at the other. The length of the string
View Solution
