A uniform wheel of radius R is set lying on a rough horizontal surface is hit by as cue is such a way that the line of action passes thruogh the centre of the shell. As a result the shelll starts movign with a linear speed v without any initial angular velocity. Find the linear speed of the shell after it starts pure rolling on the surface.
The correct Answer is:A, C
A uniform wheel of radius R is set in to rotation about its axis (case-I) at an angular speed ω. This rotating wheel is now placed on rough horizontal. Because of its friction at contact, the wheel accelerates forward and its rotation decelerates. As the rotation, if we consider the net momentum before pure rolling and after poure rolling remains constant pure. Before roling the wheel was only rotaing around its axis.
Therefore, angular momentum
=Icmω+m(V×R)
=12mR2(VR)+mVR
=32mVR
Angular momentum
mVR=12mR2ω=32mVR
→V=ωR3
Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - HC VERMACHAPTER - ROTATIONAL MECHANICSEXERCISE - Objective 2
15 Videos
- REST AND MOTION : KINEMATICSBOOK - HC VERMACHAPTER - REST AND MOTION : KINEMATICSEXERCISE - Exercises
51 Videos
- SIMPLE HARMONIC MOTIONBOOK - HC VERMACHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercises
58 Videos
Similar Questions
A thin spherical shell lying on a rough horizontal surface is hit by as cue in such a way that the line of action passes through the centre of the shell. As a result the shell starts moving with a linear speed v without any initial angualr velocity. Find the linear speed of the shell after it starts pure rolling on the surface.
View SolutionA thin spherical shell of radius R lying on a rough horizontal surface is hit sharply and horizontally by a cue. Where should it be hit so that the shell does not slip on the surface?
View Solution
Knowledge Check
A uniform solid sphere of mass M and radius R is placed on a smooth horizontal surface. It is given a horizontal impulse J at a height h above the centre of mass and sphere starts rolling. Then the value of h and speed of ccentre of mass are
Ah=25Randv=JMBh=25Randv=25JMCh=75Randv=75JMDh=75Randv=JMA heavy solid sphere is thrown on a horizontal rough surface with initial velocity u without rolling. What will be its speed, when it starts pure rolling motion ?
A3u5B2u5C5u7D2u7A sphere is moving on a smooth surface with linear speed v0 and angular velocity ω0. It finds a rough inclined surface and it starts climbing up:
 Aif v0>Rω0 friction force will act downwardsBif v0<Rω0, frictio force will act upwardsCif v0=Rω0 no friction force will actDif all above case friction will act upwards
Aif v0>Rω0 friction force will act downwardsBif v0<Rω0, frictio force will act upwardsCif v0=Rω0 no friction force will actDif all above case friction will act upwards
A solid sphere rolling on a rough horizontal surface with a linear speed v collides elastically with a fixed, smooth, vertical wall. Find the speed of the sphere after it has started pure rolling in the backward direction.
View SolutionA disc of radius R is moving on a rough horizontal surface with velocity v and angular speed ω at an instant as shown in figure. Choose the correct statement.

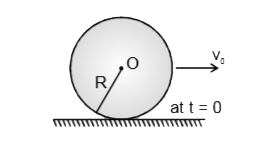
View SolutionA rigid bodyI=CMR2 is set into a motion on a rough horizontal surface with a linear speed v0 in the forward direction at time t = 0 as shown in figure. After what time slipping finally stop and pure rolling starts. Find the linear speed of the body after it starts pure rolling on the surface.
View SolutionA uniform solid sphere of radius R, rolling without sliding on a horizontal surface with an angular velocity ω0, meets a rough inclined plane of inclination θ=60∘. The sphere starts pure rolling up the plane with an angular velocity ω Find the value of ω.

View SolutionA solid sphere of radius 2.45m is rotating with an angular speed of 10rad/s. When this rotating sphere is placed on a rough horizontal surface then after sometime it starts pure rolling. Find the linear speed of the sphere after it starts pure rolling.
View Solution
