A variable force F=kx2acts on a particle which is initially at rest. Calculate the work done by the force during the displacement of the particle from x=0mtox=4m. (Assume the constant k=1Nm−2)Solution in Tamil
The correct Answer is:Work done, W=xf∫xiF(x)dx=k4∫0x2dx=64Nm
Step by step video, text & image solution for A variable force F=kx^(2)acts on a particle which is initially at rest. Calculate the work done by the force during the displacement of the particle from x=0 m "to" x= 4m. (Assume the constant k=1Nm^(-2)) by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- WORK, ENERGY AND POWERBOOK - FULL MARKSCHAPTER - WORK, ENERGY AND POWEREXERCISE - Textual Questions Solved (I. Multiple Choice Question:)
15 Videos
- WORK, ENERGY AND POWERBOOK - FULL MARKSCHAPTER - WORK, ENERGY AND POWEREXERCISE - Textual Questions Solved (II. Short Answer Questions)
5 Videos
- WAVES BOOK - FULL MARKSCHAPTER - WAVES EXERCISE - Additional Questions Solved (Numerical Problems )
10 Videos
Similar Questions
A uniform force of (2ˆi+ˆj) N acts on a particle of mass 1 kg. The particle displaces from position (3ˆj+ˆk) m to (5ˆi+3ˆj) m. The work done by the force on the particle is
View SolutionExplain how the definition of work in physics is different from general perception.
View SolutionThe fundamental frequency of a closed organ pipe is equal to the first overtone of an open organ pipe. If the length of the open pipe is 60 cm, What is the length of the closed pipe?
View SolutionA force F=−kx2(x≠0) acts on a particle in x-direction. Find the work done by this force in displacing the particle from. x=+a to x=2a. Here, k is a positive constant.
View SolutionForce acting on a particle varies with displacement as shown is Fig. Find the work done by this force on the particle from x=−4m to x = + 4m.
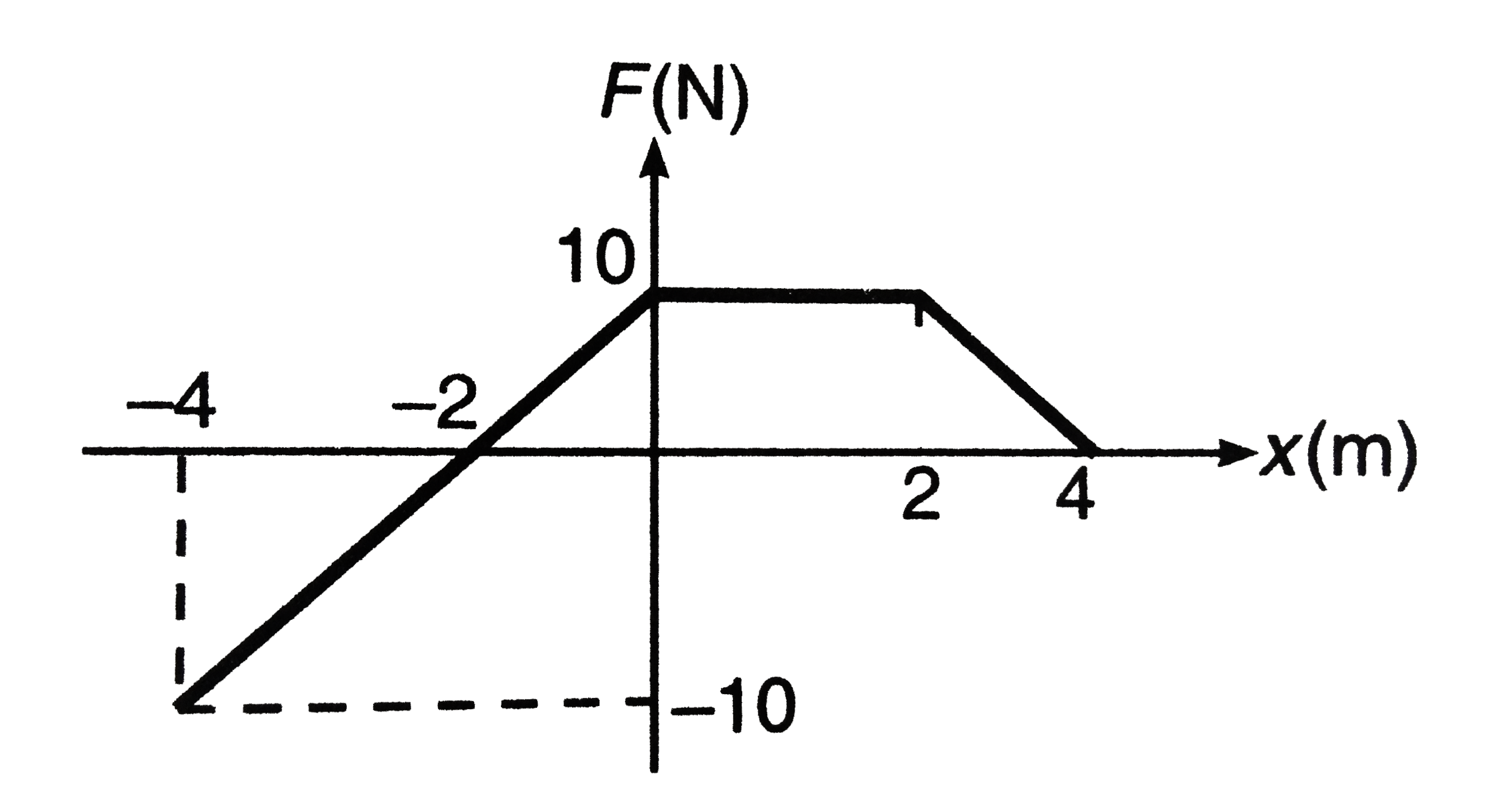 .
.
View SolutionA particle of mass m initially moving with speed v.A force acts on the particle f=kx where x is the distance travelled by the particle and k is constant. Find the speed of the particle when the work done by the force equals W.
View SolutionA particle of mass m initially at rest. A variabl force acts on the particle f=kx2 where k is a constant and x is the displacment. Find the work done by the force f when the speed of particles is v.
View Solutionबल F=kx2 द्वारा एक कण को x=aसे x=3a तक विस्थपित करने में किये गए कार्य की गणना कीजिये।
View SolutionA force of F=(0.5x+12)N acts on a particle. If x is in metre, calculate the work done by the force during the displacement of the particle from x = 0 to x = 4 m
View SolutionA force F = 0.5x + 10 acts on a particle. Here F is in newton and x is in metre. Calculate the work done by the force during the displacement of the particle from x = 0 to x = 2 metre.
View SolutionA force F=Kx2 acts on a particle at an angle of 60° with the x–axis. the work done in displacing the particle from x1 to x2 will be –
View SolutionA force F=(2+x) acts on a particle in x-direction where F is in newton and x in meter. Find the work done by this force during a displacement from 1. 0 m to x = 2.0 m.
View SolutionA force F=−kx2(x≠0) acts on a particle in x-direction. Find the work done by this force in displacing the particle from. x=+a to x=+2a. Where, k is a positive constant.
View SolutionForce acting on a particle varies with displacement as shown is Fig. Find the work done by this force on the particle from x=-4 m to x = + 4m. .
View SolutionA force F=-k/x_2(x!=0) acts on a particle in x-direction. Find the work done by this force in displacing the particle from. x = + a to x = 2a . Here, k is a positive constant.
View Solution
